25 Divided By 30
renascent
Sep 24, 2025 · 5 min read
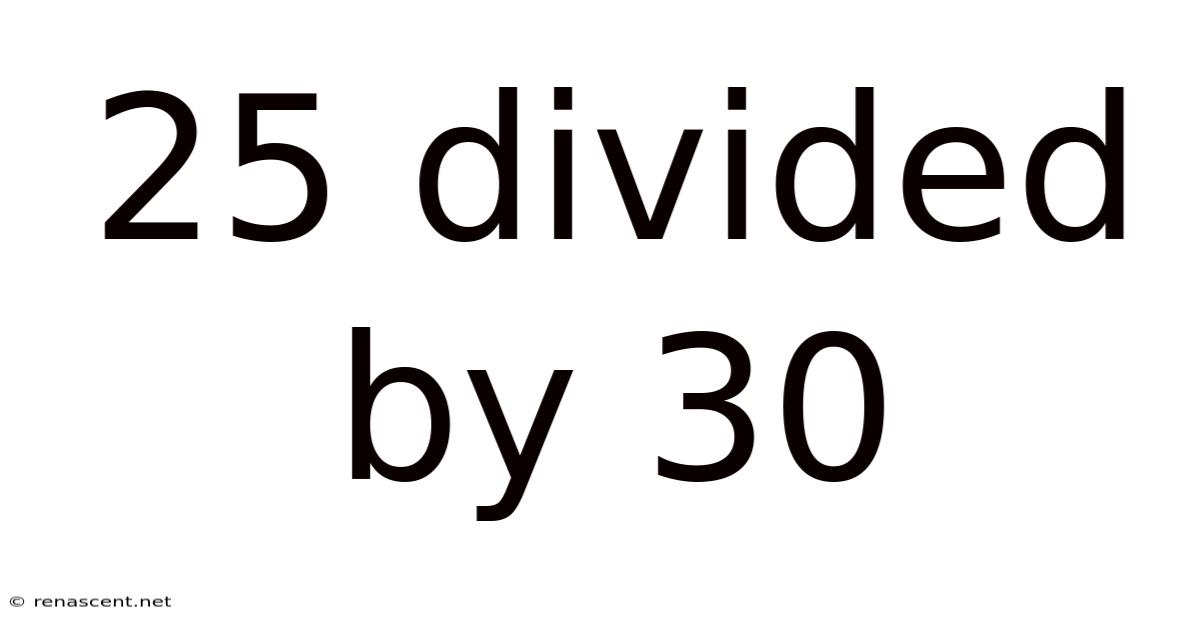
Table of Contents
Understanding 25 Divided by 30: A Deep Dive into Fractions, Decimals, and Real-World Applications
This article explores the seemingly simple calculation of 25 divided by 30, delving beyond the immediate answer to uncover the underlying mathematical principles and practical applications. We'll examine how to solve this division problem, discuss the resulting fraction and decimal, and explore its relevance in various scenarios. Understanding this seemingly basic calculation provides a solid foundation for more complex mathematical concepts.
Introduction: The Basics of Division
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It involves splitting a quantity into equal parts. In the case of 25 divided by 30 (written as 25 ÷ 30 or 25/30), we're asking: "How many times does 30 fit into 25?" The answer, intuitively, is less than one time, as 25 is smaller than 30. This leads us to the world of fractions and decimals.
Step-by-Step Calculation: Finding the Solution
To solve 25 ÷ 30, we can approach it in several ways:
1. Simplifying the Fraction:
The most straightforward method is to represent the division as a fraction: 25/30. Fractions represent a part of a whole. This fraction can be simplified by finding the greatest common divisor (GCD) of 25 and 30, which is 5. Dividing both the numerator (25) and the denominator (30) by 5, we get:
25 ÷ 5 / 30 ÷ 5 = 5/6
Therefore, 25 divided by 30 simplifies to the fraction 5/6. This is the simplest form of the fraction, meaning it cannot be reduced further.
2. Converting to a Decimal:
To express the answer as a decimal, we divide the numerator (5) by the denominator (6):
5 ÷ 6 ≈ 0.8333...
The result is a recurring decimal, meaning the digit 3 repeats infinitely. For practical purposes, we often round this to a specific number of decimal places. Rounded to two decimal places, the answer is 0.83. Rounded to three decimal places, it's 0.833. The more decimal places we use, the more precise the answer becomes, but it will always be an approximation due to the repeating decimal.
Understanding the Fraction: 5/6
The fraction 5/6 represents five out of six equal parts of a whole. Imagine a pizza cut into six slices. 5/6 represents having eaten five of those slices, leaving one slice remaining. This simple visual representation helps grasp the meaning of the fraction. It's a crucial concept in various fields, including:
- Measurement: Representing portions of measurements (e.g., 5/6 of a meter).
- Probability: Expressing the likelihood of an event (e.g., the probability of success is 5/6).
- Ratio and Proportion: Showing the relationship between two quantities.
Understanding the Decimal: 0.8333... (Recurring Decimal)
The recurring decimal 0.8333... is a representation of the fraction 5/6 in decimal form. The repeating '3' signifies that the decimal continues infinitely. This type of decimal is called a rational number because it can be expressed as a fraction of two integers. Understanding recurring decimals is important for:
- Calculations involving fractions: Converting fractions to decimals for easier calculations.
- Financial applications: Calculating percentages, interest rates, and proportions.
- Scientific measurements: Expressing precise measurements in decimal form.
Real-World Applications of 25/30
The seemingly simple calculation of 25 divided by 30 has practical applications across various fields:
-
Percentage Calculations: If you scored 25 out of 30 on a test, your score is 25/30, which simplifies to 5/6 or approximately 83.33%. This demonstrates how fractions and decimals are used to calculate percentages.
-
Scaling and Proportion: Imagine you need to reduce a recipe that originally calls for 30 grams of flour to use only 25 grams. The ratio of reduced flour to original flour is 25/30 or 5/6. This allows you to proportionally reduce the amounts of other ingredients.
-
Data Analysis: In data analysis, the ratio 25/30 could represent a proportion within a larger dataset. For example, if 25 out of 30 participants responded positively to a survey, this ratio provides valuable insights.
-
Geometry and Measurement: In geometry, this ratio could represent the proportion of two lengths or areas in a shape.
Further Exploration: More Complex Calculations
Understanding 25/30 lays the groundwork for more advanced mathematical concepts. For instance, this basic division can be extended to:
- Algebra: Solving equations involving fractions and decimals.
- Calculus: Understanding limits and derivatives which involve the manipulation of fractions.
- Statistics: Calculating probabilities, means, and standard deviations, all of which utilize fractions and decimals.
Frequently Asked Questions (FAQ)
Q: Why can't 25/30 be simplified further than 5/6?
A: Because 5 and 6 have no common factors other than 1. A fraction is in its simplest form when the numerator and denominator have no common divisors except for 1.
Q: Is 0.8333... an exact answer or an approximation?
A: It's an approximation. The decimal representation of 5/6 is infinitely long due to the recurring 3. Any finite decimal representation is an approximation.
Q: What are some other methods to solve 25 ÷ 30?
A: Long division is another method to calculate the decimal representation. However, simplifying the fraction is often quicker and more efficient for this specific problem.
Q: How does understanding this simple calculation help in more advanced mathematics?
A: Mastering fundamental operations like division with fractions and decimals is crucial for building a strong foundation in more advanced mathematical concepts such as algebra, calculus, and statistics.
Conclusion: The Importance of Foundational Math
The calculation of 25 divided by 30, while seemingly simple, offers a valuable opportunity to reinforce foundational mathematical concepts. Understanding the conversion between fractions and decimals, along with the ability to simplify fractions, is essential for success in various fields. Furthermore, the practical applications highlighted demonstrate the relevance of these seemingly basic mathematical skills in real-world situations. By mastering these fundamentals, you pave the way for tackling more complex mathematical challenges with confidence and competence. The seemingly simple equation 25/30 serves as a microcosm of the power and practicality of mathematical understanding.
Latest Posts
Latest Posts
-
350 Pound To Kg
Sep 24, 2025
-
Average Absolute Deviation Calculator
Sep 24, 2025
-
220 Grams Of Sugar
Sep 24, 2025
-
Square Root Of 63
Sep 24, 2025
-
Graph Velocity Vs Time
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 25 Divided By 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.