25 Divided By 8
renascent
Sep 20, 2025 · 5 min read
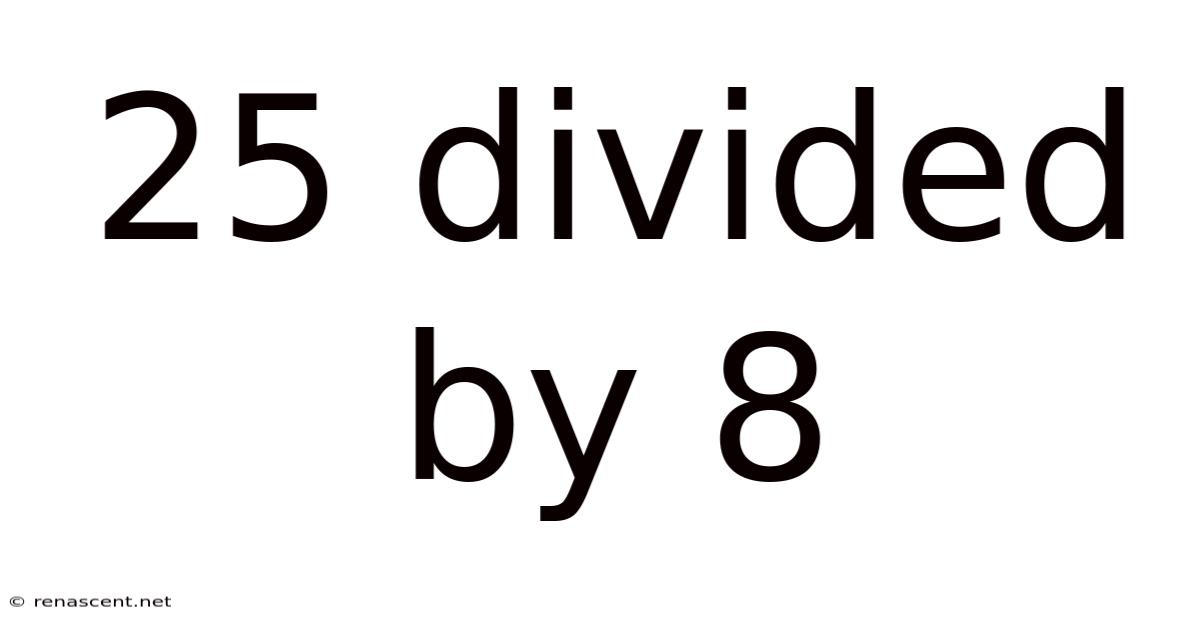
Table of Contents
Unveiling the Mystery: A Deep Dive into 25 Divided by 8
The seemingly simple question, "What is 25 divided by 8?", opens a door to a world of mathematical concepts, from basic division to the intricacies of decimals and remainders. This article will explore this seemingly straightforward calculation in detail, examining the process, its applications, and the underlying mathematical principles. We'll delve into different approaches to solving the problem, clarifying common misconceptions and enriching your understanding of division. By the end, you’ll not only know the answer but also grasp the broader mathematical context.
Understanding Division: The Foundation
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts. In the case of 25 divided by 8 (written as 25 ÷ 8 or 25/8), we're asking: "How many times does 8 fit into 25?"
Step-by-Step Calculation: Finding the Quotient and Remainder
Let's break down the calculation of 25 ÷ 8 step-by-step:
-
Initial Division: We begin by seeing how many times 8 goes into 25. 8 goes into 25 three times (8 x 3 = 24).
-
Subtraction: We subtract the product (24) from the dividend (25): 25 - 24 = 1.
-
Remainder: The result of the subtraction (1) is the remainder. This indicates that after dividing 25 into groups of 8, we have one item left over.
Therefore, 25 divided by 8 is 3 with a remainder of 1. This can be expressed as:
- 3 R1 (where R denotes remainder)
- 3 1/8 (as a mixed number, combining the whole number quotient with the remaining fraction)
Representing the Answer: Different Forms
The result of 25 divided by 8 can be represented in several ways, each useful in different contexts:
-
Mixed Number (3 1/8): This form is particularly useful when dealing with quantities that cannot be easily expressed as a decimal. It clearly shows the whole number part and the fractional part.
-
Decimal (3.125): To obtain the decimal representation, we divide the remainder (1) by the divisor (8): 1 ÷ 8 = 0.125. Adding this to the whole number quotient (3), we get 3.125. This is precise and often preferred in scientific or engineering contexts.
-
Improper Fraction (25/8): This is a representation where the numerator (25) is larger than the denominator (8). While not as intuitive as the mixed number or decimal, it is useful in certain algebraic manipulations.
Beyond the Basics: Exploring Deeper Mathematical Concepts
The simple calculation of 25 ÷ 8 offers a springboard to explore more advanced mathematical concepts:
-
Long Division: For larger numbers, long division is a systematic method to perform division. It involves a series of steps of dividing, multiplying, subtracting, and bringing down digits. While 25 ÷ 8 is easily manageable without long division, understanding this method is crucial for more complex divisions.
-
Euclidean Algorithm: This algorithm efficiently finds the greatest common divisor (GCD) of two integers. While not directly involved in calculating 25 ÷ 8, understanding the GCD helps in simplifying fractions and understanding number relationships.
-
Modular Arithmetic: The remainder (1) in 25 ÷ 8 is crucial in modular arithmetic. In modular arithmetic (modulo 8), 25 is considered equivalent to 1 (25 ≡ 1 (mod 8)). This concept has significant applications in cryptography and computer science.
-
Decimal Representation and its Limitations: While 3.125 is a precise decimal representation of 25/8, it's important to remember that some fractions (like 1/3) result in infinite repeating decimals. This highlights the limitations of decimal representation for expressing all rational numbers accurately.
-
Rational and Irrational Numbers: The result of 25 ÷ 8 (3.125) is a rational number, meaning it can be expressed as a fraction of two integers. Understanding the difference between rational and irrational numbers (like π or √2) is fundamental in advanced mathematics.
Real-World Applications: Where Division Matters
Division, and specifically the problem of 25 divided by 8, appears in numerous real-world scenarios:
-
Sharing Resources: Imagine sharing 25 candies among 8 friends. Each friend would receive 3 candies, and there would be 1 candy left over.
-
Measurement and Conversion: Converting units of measurement often involves division. For instance, converting inches to feet or centimeters to meters might require division.
-
Averaging: Calculating the average of a set of numbers involves summing the numbers and dividing by the count of numbers.
-
Rate and Ratio Problems: Many word problems involving rates (speed, cost per unit) or ratios require division to find solutions.
-
Financial Calculations: Division plays a vital role in financial calculations such as calculating unit costs, profit margins, and interest rates.
Frequently Asked Questions (FAQ)
Q: Can I express the answer as a decimal with more decimal places?
A: While 3.125 is the exact decimal representation, you can add trailing zeros (e.g., 3.125000) without changing the value. However, these additional zeros don't add any further precision.
Q: What if I divide 8 by 25?
A: Dividing 8 by 25 results in a different answer: 0.32. The order of the numbers in division significantly impacts the result.
Q: Why is the remainder important?
A: The remainder is crucial because it represents the part of the dividend that couldn't be evenly divided by the divisor. It's vital in various applications, including modular arithmetic and solving real-world problems involving sharing or distribution.
Q: Are there other methods to solve this problem besides long division?
A: Yes, you can use calculators or computer programs to perform division. You can also utilize mental math techniques if the numbers are relatively small, as in this case.
Conclusion: Mastering Division and Beyond
The simple act of dividing 25 by 8 reveals a wealth of mathematical principles and real-world applications. Understanding the different ways to represent the answer (mixed number, decimal, improper fraction), grasping the concept of the remainder, and exploring related concepts like long division and modular arithmetic provides a solid foundation for further mathematical exploration. By understanding the "why" behind the calculation, you're not just solving a problem; you're building a deeper understanding of the mathematical world around us. This seemingly simple division problem serves as a powerful illustration of how even basic arithmetic can unlock a wealth of mathematical knowledge and practical applications.
Latest Posts
Latest Posts
-
375 Grams To Oz
Sep 20, 2025
-
Peace Land And Bread
Sep 20, 2025
-
138 Pounds In Kg
Sep 20, 2025
-
Average Rice Purity Score
Sep 20, 2025
-
14 20 As A Percentage
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 25 Divided By 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.