25 Percent Of 500
renascent
Sep 14, 2025 · 5 min read
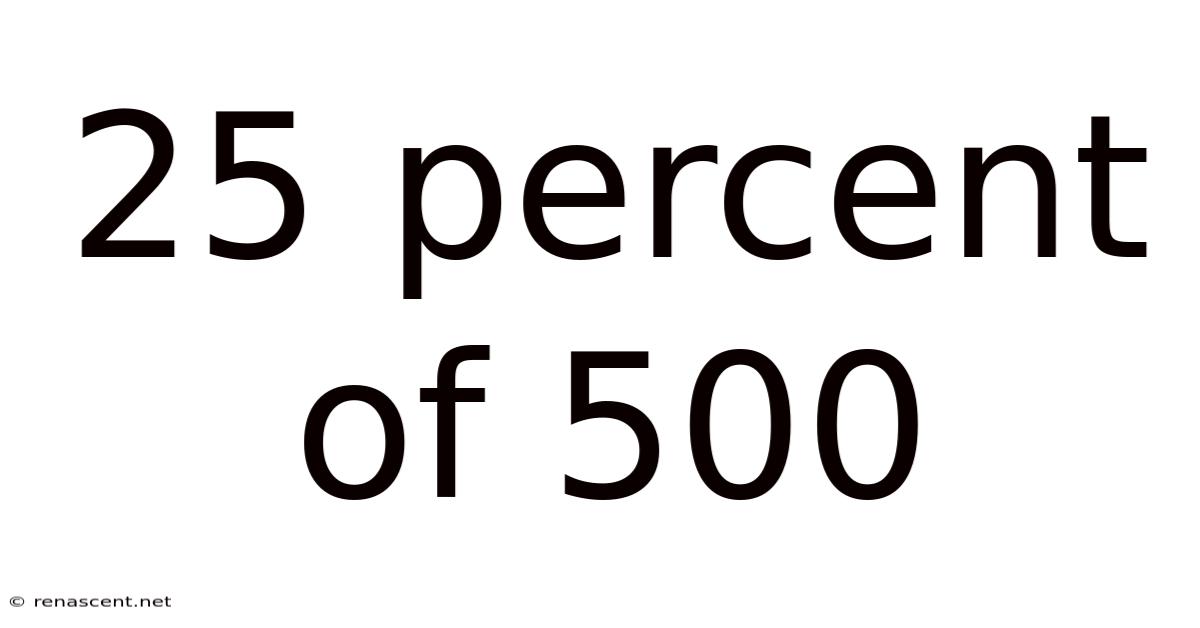
Table of Contents
Decoding 25 Percent of 500: A Comprehensive Guide to Percentages
Finding 25 percent of 500 might seem like a simple task, a quick calculation for many. But understanding the underlying principles of percentages opens doors to a wide range of applications, from everyday budgeting and shopping to complex financial calculations and scientific analysis. This article will delve deep into calculating 25% of 500, exploring different methods, explaining the core concepts, and showcasing real-world examples to solidify your understanding of percentages. We'll also address frequently asked questions and explore related percentage problems.
Understanding Percentages: The Fundamentals
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 25 percent (25%) means 25 out of 100, or 25/100. This fraction can be simplified to 1/4, indicating that 25% represents one quarter of a whole.
This fundamental understanding is crucial for tackling percentage calculations. Whether you're dealing with discounts, interest rates, tax calculations, or statistical data, the ability to convert percentages into fractions or decimals is key to accurate computation.
Method 1: The Fraction Method
This method leverages the simplified fraction representation of 25%. As mentioned earlier, 25% is equivalent to 1/4. Therefore, finding 25% of 500 is the same as finding one-quarter of 500.
- Convert the percentage to a fraction: 25% = 1/4
- Multiply the whole number by the fraction: 500 x (1/4) = 500/4
- Simplify the fraction (or perform the division): 500/4 = 125
Therefore, 25% of 500 is 125. This method is particularly intuitive and easy to visualize, especially for simpler percentages like 25%, 50%, and 75%.
Method 2: The Decimal Method
This method involves converting the percentage to its decimal equivalent before multiplying.
- Convert the percentage to a decimal: 25% = 25/100 = 0.25
- Multiply the whole number by the decimal: 500 x 0.25 = 125
Again, the result is 125. This method is often preferred for more complex percentage calculations or when using calculators, as it streamlines the process.
Method 3: The Proportion Method
The proportion method is a more formal approach, often used in more advanced mathematical contexts. It sets up a proportion to solve for the unknown value.
- Set up a proportion: Let 'x' represent 25% of 500. We can set up the proportion: 25/100 = x/500
- Cross-multiply: 25 * 500 = 100 * x
- Solve for x: 12500 = 100x => x = 12500/100 = 125
Once again, we arrive at the answer: 125. This method is useful for understanding the underlying relationship between percentages and proportions, and it's readily adaptable to various percentage problems.
Real-World Applications of Percentage Calculations
The ability to calculate percentages efficiently is invaluable in numerous real-world scenarios:
- Shopping and Sales: Calculating discounts. If a $200 item is on sale for 25% off, you'd save 25% of $200, which is $50.
- Finance and Investments: Calculating interest earned or paid, determining investment returns, and understanding loan repayments.
- Taxation: Calculating income tax, sales tax, or property tax, which are often expressed as percentages.
- Statistics and Data Analysis: Interpreting statistical data, such as survey results, where percentages are frequently used to represent proportions.
- Science and Engineering: Calculating concentrations of solutions, determining efficiency rates, and many other scientific and engineering applications.
- Cooking and Baking: Scaling recipes up or down based on percentage increases or decreases of ingredients.
Expanding Your Percentage Skills: Beyond 25% of 500
While this article focuses on calculating 25% of 500, the principles discussed extend far beyond this specific problem. Here are some related concepts and techniques to further develop your percentage calculation skills:
- Calculating other percentages: Using the methods outlined above, you can easily calculate any percentage of any number. Simply replace 25% and 500 with your desired values.
- Finding the percentage one number represents of another: For example, what percentage is 125 of 500? (Answer: 25%)
- Calculating percentage increase or decrease: This involves determining the percentage change between two numbers. For example, if a price increases from $100 to $125, the percentage increase is 25%.
- Solving for the original value: If you know the percentage and the resulting value, you can work backward to find the original amount.
Frequently Asked Questions (FAQs)
-
Q: What is the easiest method to calculate percentages?
- A: The method that works best depends on your preference and the complexity of the calculation. For simple percentages like 25%, the fraction method is often easiest to visualize. For more complex calculations or when using a calculator, the decimal method is generally more efficient.
-
Q: Can I use a calculator to find percentages?
- A: Yes! Most calculators have a percentage function (%) which simplifies the calculation. You can either directly input the calculation (e.g., 25% of 500) or convert the percentage to a decimal and then multiply.
-
Q: What if I need to calculate a percentage that isn't a simple fraction (e.g., 17% of 325)?
- A: Use the decimal method. Convert 17% to 0.17 and multiply by 325. (0.17 x 325 = 55.25)
-
Q: Are there any online tools that can help me calculate percentages?
- A: Yes, many online percentage calculators are available. These tools can be helpful for quick calculations or for checking your work.
Conclusion: Mastering Percentages – A Skill for Life
Understanding percentages is a fundamental skill applicable across various aspects of life. This article has provided a detailed explanation of calculating 25% of 500, using different methods and highlighting the core concepts. By mastering these techniques and expanding your understanding of percentages, you'll be better equipped to tackle various mathematical challenges and confidently navigate real-world situations involving percentages. Remember, practice is key. The more you work with percentages, the more comfortable and proficient you'll become. So, grab a calculator, try some practice problems, and soon you’ll be a percentage pro!
Latest Posts
Latest Posts
-
26 Divided By 30
Sep 14, 2025
-
2 Mg To Micrograms
Sep 14, 2025
-
6 7 In Decimal Form
Sep 14, 2025
-
Is Not About Money
Sep 14, 2025
-
Female Names In Argentina
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 25 Percent Of 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.