25 Percent Of 70
renascent
Sep 17, 2025 · 5 min read
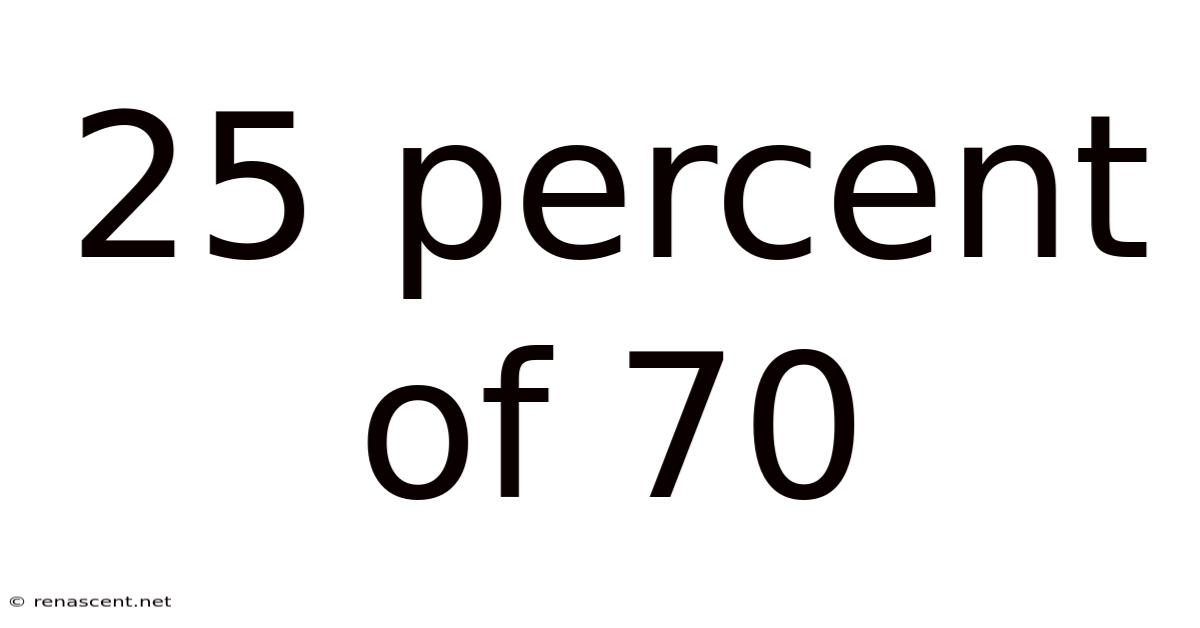
Table of Contents
Unveiling the Mystery: Calculating 25% of 70 and Beyond
Finding 25% of 70 might seem like a simple arithmetic problem, suitable only for elementary school. But this seemingly straightforward calculation opens a door to a wider understanding of percentages, fractions, decimals, and their practical applications in everyday life. This comprehensive guide will not only show you how to calculate 25% of 70 using various methods but also delve into the underlying mathematical principles and explore real-world scenarios where such calculations are vital. By the end, you'll be well-equipped to tackle similar percentage problems with confidence and a deeper appreciation for their significance.
Understanding Percentages
Before we dive into the calculation, let's solidify our understanding of percentages. A percentage is simply a fraction where the denominator is always 100. For instance, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25. Understanding this fundamental equivalence is key to solving percentage problems efficiently.
Method 1: Using the Fraction Equivalent
The easiest way to calculate 25% of 70 is to use the fraction equivalent of 25%. As mentioned above, 25% is equal to 25/100, which simplifies to 1/4. Therefore, finding 25% of 70 is the same as finding one-quarter of 70.
To do this, simply divide 70 by 4:
70 ÷ 4 = 17.5
Therefore, 25% of 70 is 17.5.
Method 2: Using Decimal Equivalents
Another straightforward method involves converting the percentage to its decimal equivalent. As we know, 25% is equal to 0.25. To find 25% of 70, we simply multiply 70 by 0.25:
70 x 0.25 = 17.5
This method yields the same result as the fraction method, confirming the accuracy of our calculations. This method is particularly useful when working with percentages that don't easily convert to simple fractions.
Method 3: The Proportion Method
This method is excellent for understanding the underlying relationship between percentages and proportions. We can set up a proportion:
25/100 = x/70
Where 'x' represents the value we're trying to find (25% of 70). To solve for 'x', we cross-multiply:
25 * 70 = 100 * x
1750 = 100x
Now, divide both sides by 100:
x = 1750 / 100 = 17.5
Again, we arrive at the answer: 17.5. This method is particularly helpful when dealing with more complex percentage problems.
Method 4: Using a Calculator
For those who prefer a more direct approach, a simple calculator can efficiently handle the calculation. Simply enter "70 x 0.25" or "70 x 25%" (depending on your calculator's functionality) to obtain the answer: 17.5. While this is the quickest method, understanding the underlying mathematical principles is crucial for solving more complex problems and for developing a strong mathematical foundation.
Real-World Applications of Percentage Calculations
Understanding percentage calculations isn't just about solving math problems; it's a crucial skill applicable to numerous real-world scenarios. Here are a few examples:
-
Sales and Discounts: Imagine a store offering a 25% discount on a $70 item. Using the methods described above, you can quickly determine the discount amount ($17.50) and the final price ($52.50).
-
Calculating Tips: Determining a 25% tip on a $70 restaurant bill involves the same calculation. You would owe $17.50 in tip.
-
Financial Calculations: Percentages are fundamental in finance, used to calculate interest rates, returns on investments, and taxes. Understanding percentage calculations is crucial for making informed financial decisions.
-
Data Analysis: Percentages are frequently used to represent data in charts and graphs, making it easier to visualize and understand trends and proportions. For example, understanding that 25% of a survey group chose a particular option provides valuable insight.
-
Scientific Applications: Percentages play a crucial role in various scientific fields, including chemistry, physics, and biology, where they are used to express concentrations, yields, and other important parameters.
Expanding Your Understanding: Beyond 25% of 70
While we've focused on calculating 25% of 70, the principles discussed apply to any percentage calculation. Let's explore some variations:
-
Calculating other percentages of 70: To find any percentage of 70, simply convert the percentage to its decimal equivalent and multiply by 70. For example, 15% of 70 would be 70 * 0.15 = 10.5.
-
Calculating 25% of different numbers: The same methods can be applied to find 25% of any number. For example, 25% of 120 is 120 * 0.25 = 30.
-
Finding the original amount: If you know a percentage and the resulting value, you can work backward to find the original amount. For example, if 25% of a number is 17.5, divide 17.5 by 0.25 to get the original number (70).
Frequently Asked Questions (FAQs)
Q: What is the easiest way to calculate percentages?
A: The easiest method depends on the specific percentage and your comfort level with different mathematical operations. Using fraction equivalents is often easiest for simple percentages like 25%, 50%, and 75%. Converting to decimals is generally more versatile for other percentages.
Q: How can I improve my percentage calculation skills?
A: Practice is key! Start with simple problems and gradually increase the complexity. Understanding the underlying principles of fractions and decimals is also crucial. You can find numerous online resources and practice exercises to hone your skills.
Q: Are there any online tools to calculate percentages?
A: Yes, numerous online percentage calculators are available. However, understanding the methods discussed here is more valuable than relying solely on calculators, as it enhances your mathematical understanding and problem-solving capabilities.
Q: Why is it important to understand percentage calculations?
A: Percentage calculations are essential for everyday life, from managing finances and shopping to interpreting data and understanding scientific concepts. It's a fundamental skill with wide-ranging applications.
Conclusion
Calculating 25% of 70, while seemingly simple, provides a springboard for understanding the broader world of percentages. By mastering the different methods—using fractions, decimals, proportions, or a calculator—you equip yourself not just with a simple calculation but with a vital skill applicable to numerous aspects of life. Remember, the true value lies not only in getting the correct answer (17.5) but also in grasping the underlying principles and expanding your mathematical reasoning. So, embrace the challenge, practice consistently, and watch your confidence in handling percentage calculations soar!
Latest Posts
Latest Posts
-
49 C To Fahrenheit
Sep 17, 2025
-
188 Pounds In Kg
Sep 17, 2025
-
192 Minutes In Hours
Sep 17, 2025
-
315 Minutes To Hours
Sep 17, 2025
-
147 Kg In Lbs
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 25 Percent Of 70 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.