26 Squared 24 Squared
renascent
Sep 21, 2025 · 6 min read
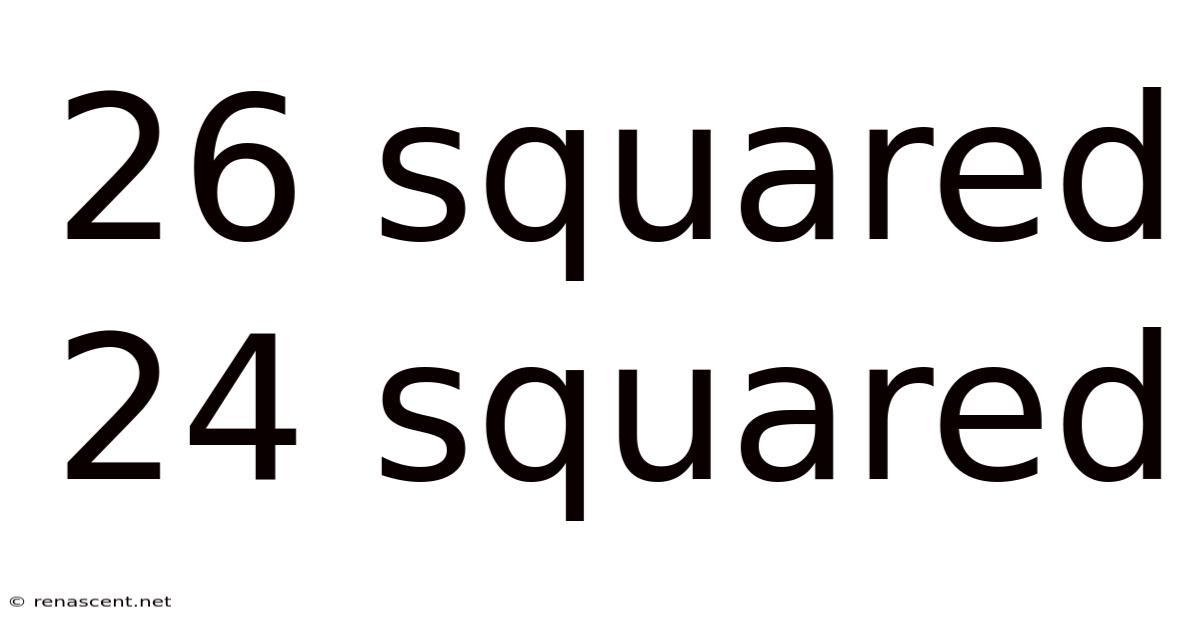
Table of Contents
Exploring the Squares of 26 and 24: A Deep Dive into Squares, Perfect Squares, and Their Applications
This article delves into the mathematical concept of squaring numbers, specifically focusing on 26 squared (26²) and 24 squared (24²). We will explore the calculations, discuss the properties of perfect squares, and examine their applications in various fields, from basic arithmetic to advanced geometric calculations. Understanding squares is fundamental to numerous mathematical concepts, and this comprehensive guide aims to enhance your understanding of this core concept.
Introduction: Understanding Squares and Perfect Squares
In mathematics, squaring a number means multiplying the number by itself. For instance, 26 squared (26²) means 26 x 26, and 24 squared (24²) means 24 x 24. The result of squaring a number is called a perfect square. Perfect squares are numbers that can be obtained by squaring an integer (a whole number). Understanding perfect squares is crucial for various mathematical operations and problem-solving. This article will provide a detailed explanation of how to calculate 26² and 24², along with a broader understanding of their significance within mathematics.
Calculating 26 Squared (26²)
There are several ways to calculate 26 squared:
-
Direct Multiplication: The most straightforward method is to perform the multiplication directly: 26 x 26 = 676. This can be done using traditional multiplication methods learned in elementary school.
-
Using the Difference of Squares Formula: This method leverages the algebraic identity (a+b)(a-b) = a² - b². We can rewrite 26 as (25 + 1). Then, 26² = (25 + 1)² = 25² + 2(25)(1) + 1² = 625 + 50 + 1 = 676. This method is useful for squaring numbers close to multiples of 10.
-
Using the Distributive Property: We can break down 26 into 20 + 6 and apply the distributive property: (20 + 6)² = (20 + 6)(20 + 6) = 20² + 2(20)(6) + 6² = 400 + 240 + 36 = 676. This method is helpful for mentally calculating squares of two-digit numbers.
Calculating 24 Squared (24²)
Similar to calculating 26 squared, we can use various methods to find 24 squared:
-
Direct Multiplication: The most straightforward approach is to multiply 24 by itself: 24 x 24 = 576.
-
Using the Difference of Squares Formula: We can express 24 as (25 - 1). Then, 24² = (25 - 1)² = 25² - 2(25)(1) + 1² = 625 - 50 + 1 = 576. This method efficiently calculates the square of numbers close to multiples of 10 or easily squared numbers.
-
Using the Distributive Property: Breaking down 24 into 20 + 4, we can use the distributive property: (20 + 4)² = (20 + 4)(20 + 4) = 20² + 2(20)(4) + 4² = 400 + 160 + 16 = 576. This method offers an alternative approach to mental calculation.
Properties of Perfect Squares
Perfect squares possess several interesting mathematical properties:
-
Ending Digits: Perfect squares can only end in 0, 1, 4, 5, 6, or 9. They never end in 2, 3, 7, or 8. This property can be used to quickly eliminate possibilities when dealing with square root problems.
-
Sum of Odd Numbers: Every perfect square is the sum of consecutive odd numbers. For example, 1² = 1, 2² = 1 + 3, 3² = 1 + 3 + 5, 4² = 1 + 3 + 5 + 7, and so on.
-
Geometric Representation: Perfect squares can be represented geometrically as square shapes. For example, 25 (5²) can be represented as a 5x5 grid of squares.
-
Algebraic Properties: Perfect squares play a crucial role in various algebraic identities and manipulations. They are often encountered when factoring quadratic equations and solving algebraic problems.
Applications of Squares in Various Fields
The concept of squaring numbers finds numerous applications in various fields:
-
Geometry: Calculating areas of squares and rectangles involves squaring the length of their sides. The Pythagorean theorem (a² + b² = c²) relies heavily on the concept of squares to determine the length of the hypotenuse of a right-angled triangle. This is fundamental to surveying, construction, and many other fields.
-
Physics: Many physics formulas involve squaring quantities, such as the calculation of kinetic energy (KE = ½mv²), where velocity is squared. This is just one example among many in classical mechanics, electromagnetism, and other areas of physics.
-
Statistics: In statistics, variance and standard deviation calculations involve squaring the deviations from the mean. This helps to quantify the spread or dispersion of data.
-
Computer Science: In computer graphics and image processing, squaring values is common in calculations involving pixel coordinates and distances. Hashing algorithms often utilize squaring operations for data manipulation.
-
Finance: Compound interest calculations involve squaring and higher powers of numbers, reflecting the exponential growth of investments over time.
-
Everyday Life: Many practical applications utilize the concept of squares without explicit mention. Consider calculating the area of a floor to buy tiles, determining the size of a square garden plot, or estimating the distance traveled based on speed and time (distance = speed x time, and speed often involves squared units like m/s²).
Further Exploration: Beyond 26² and 24²
While this article focuses on 26² and 24², understanding the broader concept of squaring numbers is essential. This includes exploring:
-
Square Roots: The inverse operation of squaring a number is finding its square root. Understanding the relationship between squares and square roots is crucial for various mathematical problems.
-
Higher Powers: Cubing (raising to the power of 3), raising to the power of 4, and higher powers are extensions of the concept of squaring. These higher powers also find applications in various fields.
-
Negative Numbers: Squaring negative numbers results in positive perfect squares. Understanding this property is essential for algebraic manipulations.
-
Irrational Numbers: Not all numbers have perfect square roots. Irrational numbers, like the square root of 2, are numbers that cannot be expressed as a ratio of two integers.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between 26² and 24²?
- A: 26² = 676 and 24² = 576. The difference is 676 - 576 = 100.
-
Q: Are there any shortcuts to calculate squares mentally?
- A: Yes, there are several mental math tricks. The difference of squares formula is helpful for numbers close to easily squared numbers (like multiples of 10). The distributive property can also be used for two-digit numbers. Practice is key to mastering these techniques.
-
Q: What are some real-world examples where squaring is used?
- A: Many examples exist. Calculating the area of a square, determining the kinetic energy of a moving object, and calculating the distance traveled at a constant acceleration all involve squaring numbers.
Conclusion: The Enduring Significance of Squares
The seemingly simple operation of squaring numbers holds immense significance across diverse fields. From basic arithmetic to advanced physics and engineering, understanding squares and their properties is fundamental. This article provided a comprehensive overview of calculating 26² and 24², explored the properties of perfect squares, and highlighted their widespread applications. By grasping the core concepts explained here, you can strengthen your mathematical foundation and expand your problem-solving capabilities. Further exploration into related topics like square roots and higher powers will enhance your mathematical knowledge even further. The journey of understanding mathematics is continuous, and exploring the seemingly simple concepts like squares often reveals a surprising depth and elegance.
Latest Posts
Latest Posts
-
1 4 Of 20
Sep 21, 2025
-
80 5 Kg In Pounds
Sep 21, 2025
-
166 Min To Hours
Sep 21, 2025
-
Rudy In Ice Age
Sep 21, 2025
-
150 Gm To Oz
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 26 Squared 24 Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.