27/30 As A Percent
renascent
Sep 17, 2025 · 5 min read
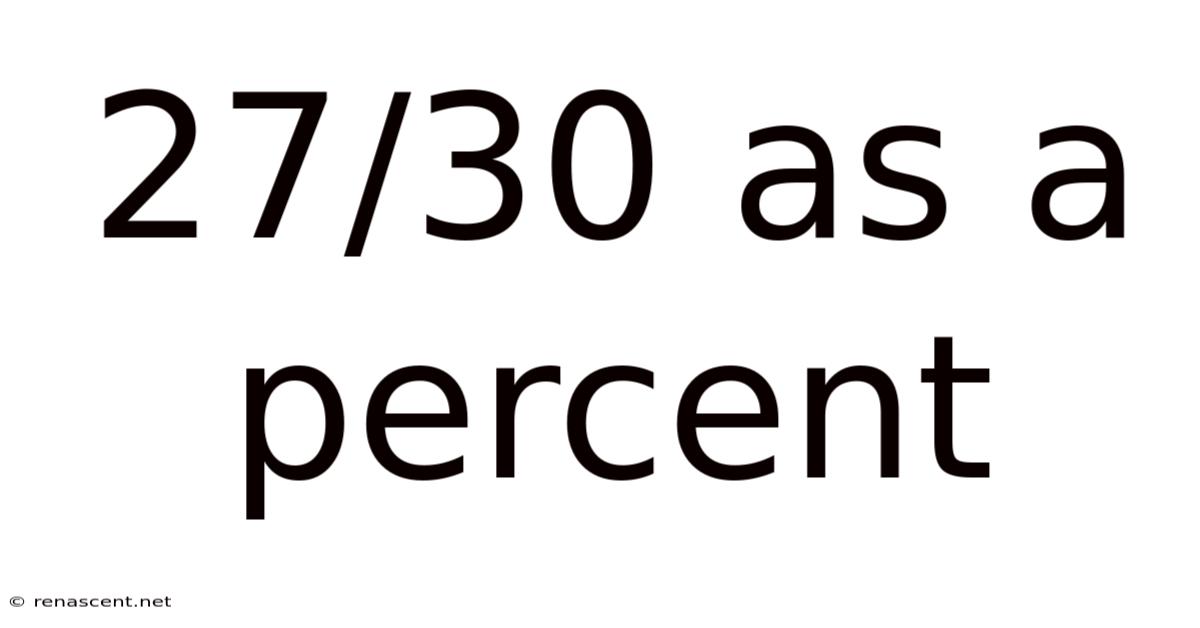
Table of Contents
27/30 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced statistical analysis. This comprehensive guide will not only show you how to calculate 27/30 as a percentage but also equip you with the knowledge to tackle similar conversions with confidence. We'll delve into the underlying principles, provide step-by-step instructions, explore real-world examples, and address frequently asked questions. By the end, you'll not only know the answer but also understand the why behind the calculation.
Understanding Fractions and Percentages
Before diving into the conversion of 27/30, let's refresh our understanding of fractions and percentages.
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). In the fraction 27/30, 27 represents the part and 30 represents the whole.
A percentage is a way of expressing a fraction as a portion of 100. The symbol "%" signifies "per hundred" or "out of 100". For example, 50% means 50 out of 100, or 50/100.
Converting 27/30 to a Percentage: Step-by-Step
Converting a fraction to a percentage involves two main steps:
Step 1: Convert the Fraction to a Decimal
To convert a fraction to a decimal, simply divide the numerator by the denominator. In this case:
27 ÷ 30 = 0.9
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol. Therefore:
0.9 × 100 = 90%
Therefore, 27/30 is equal to 90%.
Simplifying the Fraction First (Optional but Recommended)
While the above method works perfectly well, simplifying the fraction before conversion can make the calculation easier, especially with larger numbers. Let's see how:
The fraction 27/30 can be simplified by finding the greatest common divisor (GCD) of 27 and 30. The GCD of 27 and 30 is 3. Dividing both the numerator and denominator by 3, we get:
27 ÷ 3 = 9 30 ÷ 3 = 10
This simplifies the fraction to 9/10. Now, converting 9/10 to a decimal:
9 ÷ 10 = 0.9
And converting the decimal to a percentage:
0.9 × 100 = 90%
As you can see, we arrive at the same answer, 90%, but the simplified fraction made the division step significantly easier. This simplification is a valuable technique for handling more complex fraction-to-percentage conversions.
Real-World Applications
Understanding fraction-to-percentage conversions is crucial in various real-world scenarios:
- Academic Performance: If a student answers 27 out of 30 questions correctly on a test, their score is 90%.
- Sales and Discounts: A store offering a 10% discount on an item priced at $30 would reduce the price by $3 (10% of $30), resulting in a final price of $27.
- Financial Calculations: Calculating interest rates, profit margins, or tax percentages often involves converting fractions to percentages.
- Data Analysis: Representing data in percentage form makes it easier to understand and compare different proportions.
Understanding the Concept of Proportion
The conversion from 27/30 to 90% highlights the concept of proportion. A fraction represents a proportion of a whole. Converting to a percentage simply expresses this proportion as a fraction of 100. This underlying principle is fundamental to numerous mathematical and real-world applications. It allows us to compare different fractions and easily visualize the relative sizes of parts compared to the whole.
Advanced Techniques and Further Exploration
While the method described above is sufficient for most basic calculations, more advanced techniques exist for handling complex fractions or percentages. These include:
- Using proportions: Setting up a proportion, such as x/100 = 27/30, allows you to solve for x, which represents the percentage.
- Using a calculator: Most calculators have a fraction-to-decimal or percentage conversion function, simplifying the calculation.
- Understanding ratios: Understanding ratios and proportions allows you to intuitively grasp the relationship between fractions and percentages.
Exploring these advanced techniques can broaden your understanding of the subject and enhance your problem-solving skills.
Frequently Asked Questions (FAQ)
Q: Can I convert any fraction to a percentage?
A: Yes, any fraction can be converted to a percentage using the methods described above.
Q: What if the fraction is an improper fraction (numerator is larger than denominator)?
A: Improper fractions, when converted to decimals, will result in decimals greater than 1. When converting to a percentage, you will get a percentage greater than 100%. This is perfectly acceptable and simply indicates that the part is larger than the whole, which is possible in certain contexts.
Q: What if the fraction involves decimals in the numerator or denominator?
A: You can still follow the same steps. Convert the decimal to a fraction first, then proceed with the division and multiplication steps.
Q: Why is understanding percentages important?
A: Percentages provide a standardized way to compare proportions, making it easier to understand and interpret data across various fields like finance, science, and everyday life. They are universally understood and provide a common basis for comparison.
Q: Are there any shortcuts for converting fractions to percentages?
A: If the denominator of the fraction is a factor of 100 (such as 10, 20, 25, 50), you can often mentally convert it to a percentage without doing the full calculation. For example, 1/10 is 10%, 1/20 is 5%, and 1/25 is 4%. This is a useful mental math technique for quick estimations.
Conclusion
Converting 27/30 to a percentage, resulting in 90%, is a straightforward process involving two simple steps: converting the fraction to a decimal and then the decimal to a percentage. However, the underlying principles—understanding fractions, decimals, percentages, and proportions—are far more profound and applicable across various areas of life and study. Mastering these concepts is key to developing strong mathematical skills and problem-solving abilities. Remember to simplify fractions whenever possible to make calculations easier. Practice these techniques regularly, and you'll build confidence in tackling any fraction-to-percentage conversion. By understanding the "why" behind the calculations, you'll move beyond rote memorization to a deep understanding of mathematical concepts.
Latest Posts
Latest Posts
-
5 6 Divided By 8
Sep 17, 2025
-
125 Miles To Km
Sep 17, 2025
-
1 4th Of 32
Sep 17, 2025
-
Frida Kahlo Monkey Portrait
Sep 17, 2025
-
98 1 F To C
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 27/30 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.