27 Divided By 6
renascent
Sep 16, 2025 · 6 min read
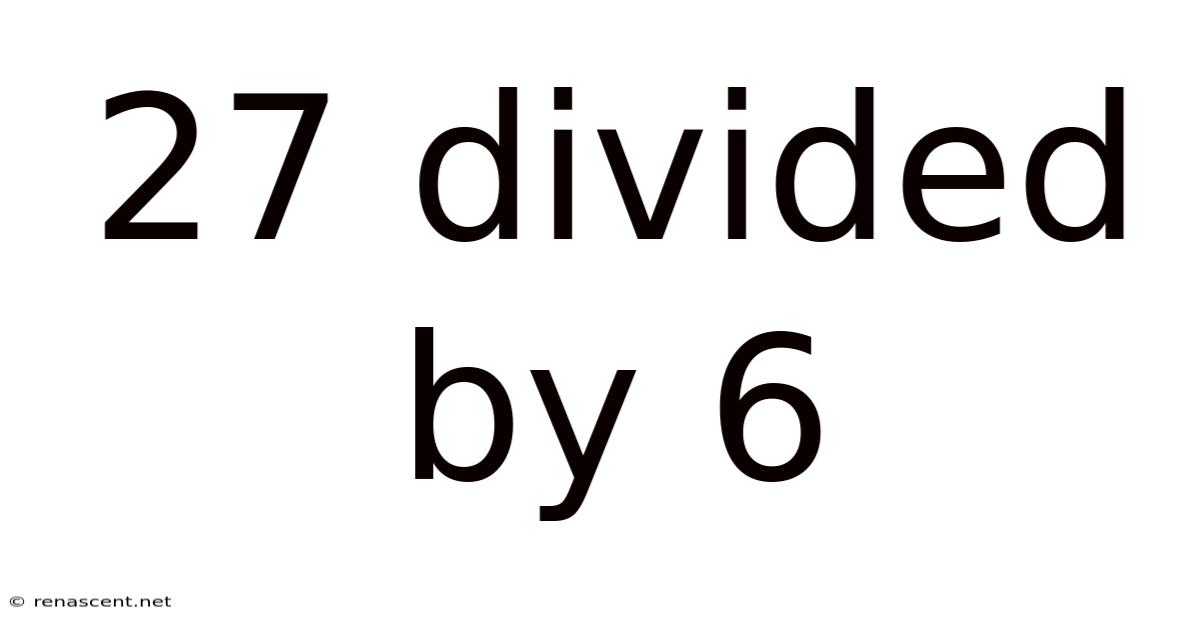
Table of Contents
Unveiling the Mystery: A Deep Dive into 27 Divided by 6
This article explores the seemingly simple calculation of 27 divided by 6, delving far beyond the basic answer to uncover the underlying mathematical principles and practical applications. Understanding this seemingly straightforward division problem offers a gateway to grasping more complex concepts in arithmetic, algebra, and even real-world scenarios. We'll examine various methods for solving the problem, explore the meaning of remainders, and discuss how this seemingly simple calculation can be applied in everyday life.
Introduction: Beyond the Basic Answer
At first glance, 27 divided by 6 might appear trivial. A quick calculation reveals the answer: 4 with a remainder of 3. However, this simple calculation provides a rich opportunity to understand fundamental mathematical concepts. This article will delve into the various methods of performing this division, explaining the significance of the quotient (4) and the remainder (3), and showing how this seemingly simple calculation can be applied in different contexts.
Method 1: Long Division – A Classic Approach
The traditional method for solving 27 ÷ 6 is long division. This method provides a step-by-step approach to understanding the process:
-
Set up the problem: Write 6 (the divisor) outside the long division symbol and 27 (the dividend) inside.
-
Divide: How many times does 6 go into 2? It doesn't go in at all, so we move to the next digit. How many times does 6 go into 27? It goes in 4 times (6 x 4 = 24). Write the 4 above the 7.
-
Multiply: Multiply the quotient (4) by the divisor (6): 4 x 6 = 24. Write this below the 27.
-
Subtract: Subtract the result (24) from the dividend (27): 27 - 24 = 3.
-
Remainder: The result (3) is the remainder. It is less than the divisor (6), indicating we have completed the division.
Therefore, 27 ÷ 6 = 4 with a remainder of 3. This is often written as 4 R 3 or 4⅓.
Method 2: Repeated Subtraction
Another way to approach this is through repeated subtraction. We repeatedly subtract the divisor (6) from the dividend (27) until we reach a number less than the divisor:
- 27 - 6 = 21
- 21 - 6 = 15
- 15 - 6 = 9
- 9 - 6 = 3
We subtracted 6 four times before reaching a number less than 6. This means the quotient is 4, and the remaining 3 is the remainder. This method highlights the underlying concept of division as repeated subtraction.
Method 3: Fractions – Expressing the Remainder as a Fraction
The remainder can be expressed as a fraction. The remainder (3) becomes the numerator, and the divisor (6) becomes the denominator. Thus, 27 ÷ 6 = 4 3/6. This fraction can be simplified to 4 ½ by dividing both the numerator and the denominator by their greatest common divisor (3). This representation offers a more precise answer than simply stating "4 R 3."
Understanding the Quotient and Remainder
The quotient (4) represents the number of times the divisor (6) goes into the dividend (27) completely. The remainder (3) represents the amount left over after the complete divisions. In the context of dividing 27 objects into groups of 6, we would have 4 complete groups and 3 objects remaining.
Real-World Applications
The concept of division with remainders appears frequently in everyday life:
- Sharing: If you have 27 cookies and want to share them equally among 6 friends, each friend gets 4 cookies, and you have 3 cookies left.
- Measurement: If you need to cut a 27-inch piece of ribbon into 6-inch pieces, you can cut 4 pieces, and you'll have a 3-inch piece remaining.
- Pricing: If an item costs $27 and you want to divide the cost equally among 6 people, each person pays $4.50 ($4 with a remainder expressed as 50 cents).
- Time: Converting minutes to hours: 27 minutes is equal to 0.45 hours (45 minutes is 3/4 of an hour, hence 27 minutes is 27/60 or 9/20 of an hour)
The Significance of Remainders
The remainder is not simply a leftover; it provides crucial information. In some contexts, it's just as important as the quotient. Consider these scenarios:
- Modular Arithmetic: In modular arithmetic (a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value—the modulus), the remainder is the primary focus. For example, in modulo 6 arithmetic, 27 is equivalent to 3 (since 27 ÷ 6 leaves a remainder of 3). This system is used in cryptography and computer science.
- Cyclic Processes: In scenarios involving cyclical processes (like days of the week or hours on a clock), the remainder indicates the position within the cycle. For example, if an event occurs every 6 days, the remainder when dividing the number of days passed by 6 tells us the day of the week the event will occur.
Decimal Representation: Beyond Whole Numbers
While the whole number quotient and remainder are useful, expressing the result as a decimal provides a different perspective. Using a calculator or continued long division, 27 ÷ 6 ≈ 4.5. This decimal representation shows the exact portion of the divisor contained within the dividend.
Beyond the Basics: Extending the Concepts
This seemingly simple problem opens doors to more complex mathematical ideas:
-
Algebra: The concept of division with remainders can be expressed algebraically. We can represent the division of 27 by 6 as 27 = 6q + r, where 'q' is the quotient and 'r' is the remainder (0 ≤ r < 6). This equation forms the basis for understanding more complex algebraic concepts involving remainders and divisibility.
-
Number Theory: Number theory delves into the properties of integers and their relationships. Concepts like divisibility, prime numbers, and modular arithmetic are fundamental to number theory, and understanding the division of 27 by 6 lays a foundation for exploring these fascinating areas.
-
Computer Science: Remainders play a crucial role in computer algorithms and programming. Operations such as finding the modulo (remainder) of a number are used in various applications, including hash tables, random number generators, and cryptographic techniques.
Frequently Asked Questions (FAQ)
-
What is the most efficient way to solve 27 divided by 6? While long division provides a methodical approach, for this specific problem, recognizing that 6 x 4 = 24 and then finding the remainder (27 - 24 = 3) is often the quickest method.
-
Can the remainder ever be larger than the divisor? No, by definition, the remainder must be smaller than the divisor. If the remainder is larger, it means the division is incomplete.
-
Why is expressing the remainder as a fraction sometimes preferred? A fractional representation provides a more precise and complete answer than simply stating the remainder. It expresses the portion of the divisor that is not fully contained in the dividend.
-
What if I'm dividing larger numbers? The long division method, or using a calculator, remains the most practical approach for larger numbers. However, the underlying principles—the concept of the quotient and remainder—remain the same.
Conclusion: A Foundation for Deeper Understanding
The seemingly simple calculation of 27 divided by 6 offers a powerful entry point to understanding core mathematical concepts. By exploring different methods, analyzing the significance of the quotient and remainder, and examining real-world applications, we've uncovered the rich depth hidden within this basic arithmetic problem. This exploration serves as a strong foundation for tackling more complex mathematical concepts and applications across various disciplines. The seemingly simple act of dividing 27 by 6 unlocks a world of mathematical possibilities. It is a testament to the beauty of mathematics that even the simplest operations can reveal profound insights and connections.
Latest Posts
Latest Posts
-
63 2 Kg To Pounds
Sep 17, 2025
-
4 24 Equivalent Fractions
Sep 17, 2025
-
150 Miles In Kilometers
Sep 17, 2025
-
Australia Tropic Of Capricorn
Sep 17, 2025
-
2 3 Of 46
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 27 Divided By 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.