2x 3 X 5
renascent
Sep 17, 2025 · 6 min read
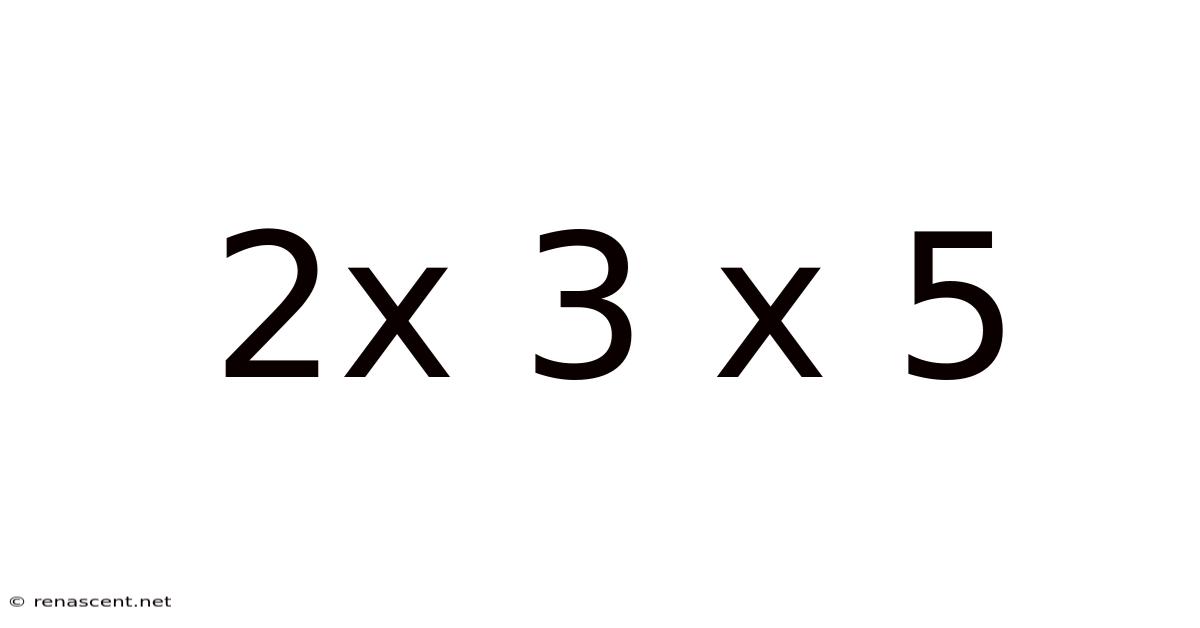
Table of Contents
Decoding 2 x 3 x 5: Exploring the Fundamentals of Multiplication and its Applications
This article delves into the seemingly simple mathematical expression "2 x 3 x 5," unraveling its significance beyond a basic arithmetic calculation. We'll explore the fundamental principles of multiplication, examine the specific result of this equation, and demonstrate its practical applications across various fields. Understanding this seemingly simple equation lays the groundwork for more complex mathematical concepts and problem-solving. We'll cover everything from basic arithmetic to its role in more advanced mathematical fields.
Understanding the Basics: Multiplication as Repeated Addition
Before diving into 2 x 3 x 5, let's solidify our understanding of multiplication. At its core, multiplication is simply a shortcut for repeated addition. For example, 2 x 3 means adding two, three times: 2 + 2 + 2 = 6. This fundamental concept is crucial because it allows us to efficiently handle larger numbers and more complex calculations.
Calculating 2 x 3 x 5: A Step-by-Step Approach
Now, let's tackle 2 x 3 x 5. Because multiplication is associative (meaning the order of operations doesn't change the result), we can solve this in several ways. Let's illustrate two common approaches:
Method 1: Left-to-Right Calculation
- 2 x 3 = 6: We start by multiplying the first two numbers.
- 6 x 5 = 30: Then, we multiply the result by the third number.
Therefore, 2 x 3 x 5 = 30.
Method 2: Using the Commutative Property
Multiplication is also commutative, meaning the order of the numbers doesn't affect the final product. We can rearrange the numbers for easier calculation:
- 2 x 5 = 10: This is a simpler multiplication than 2 x 3.
- 10 x 3 = 30: Multiplying by 3 is also straightforward.
Again, the result is 30. This illustrates the flexibility of multiplication and allows us to choose the method that feels most intuitive or efficient.
The Number 30: Prime Factorization and its Significance
The result of 2 x 3 x 5 is 30. This number holds a particular significance in mathematics due to its prime factorization. Prime factorization is the process of breaking down a number into its prime factors – numbers that are only divisible by 1 and themselves. The prime factors of 30 are 2, 3, and 5.
- 2: An even number, the smallest prime number.
- 3: An odd number, the second smallest prime number.
- 5: An odd number, the third smallest prime number.
This prime factorization is unique to 30. No other combination of prime numbers will multiply to give 30. This uniqueness is fundamental to number theory and has applications in cryptography and other advanced mathematical fields.
Applications of Multiplication and the Number 30 in Real-Life Scenarios
The simple calculation 2 x 3 x 5, and the resultant number 30, might seem abstract, but its applications are widespread and surprisingly relevant:
-
Everyday Calculations: Imagine you're buying groceries. You need 2 bags of apples with 3 apples each bag, and each apple costs 5 dollars. The total cost is 2 x 3 x 5 = $30. This shows how multiplication simplifies everyday financial calculations.
-
Geometry and Measurement: The area of a rectangular prism (a 3D shape like a box) can be calculated using multiplication. If the dimensions of the box are 2 units, 3 units, and 5 units, then the volume is 2 x 3 x 5 = 30 cubic units. This is a fundamental concept in geometry and engineering.
-
Data Analysis: In data analysis and statistics, multiplication is used extensively. Consider a scenario where you are collecting data from a survey. If you have 2 survey questions, each with 3 possible answers, and you have 5 different groups of respondents, the total number of possible responses is 2 x 3 x 5 = 30. This simple calculation can help determine the sample size for statistical analysis.
-
Combinatorics and Probability: Multiplication plays a crucial role in combinatorics, the study of counting. If you have 2 shirts, 3 pants, and 5 pairs of shoes, the total number of outfits you can create is 2 x 3 x 5 = 30. This is a fundamental concept in probability theory as well.
-
Computer Science and Programming: Multiplication is a fundamental operation in computer programming. It is used in algorithms, data structures, and various programming tasks. Understanding how multiplication works is crucial for efficient code writing and problem-solving.
-
Physics and Engineering: In physics and engineering, multiplication is used for calculations involving forces, velocities, and energy. Many physical laws and formulas involve multiplication as a core component.
-
Financial Modeling: In finance, understanding multiplication is crucial for compound interest calculations, portfolio diversification strategies, and risk assessment models.
Expanding on the Concept: Exploring Beyond Basic Arithmetic
While 2 x 3 x 5 provides a straightforward example, the principles of multiplication extend far beyond this simple equation. Consider the following:
-
Larger Numbers: The same principles apply when dealing with much larger numbers, and efficient calculation methods like long multiplication become increasingly important.
-
Decimals and Fractions: Multiplication works equally well with decimals and fractions, requiring slightly different techniques but based on the same underlying concepts of repeated addition.
-
Algebra: Multiplication is a core component of algebra, where variables represent unknown quantities. Solving algebraic equations often involves manipulating multiplicative expressions.
-
Calculus: Even in calculus, a branch of mathematics dealing with continuous change, multiplication forms the basis of many crucial operations and formulas.
Frequently Asked Questions (FAQ)
Q: What is the order of operations when dealing with multiple multiplications?
A: As previously discussed, multiplication is associative and commutative. You can perform the multiplications in any order and arrive at the same result.
Q: Is there a difference between 2 x 3 x 5 and 5 x 3 x 2?
A: No. Due to the commutative property of multiplication, changing the order of the numbers does not change the final product. Both expressions equal 30.
Q: How can I improve my multiplication skills?
A: Practice is key. Start with smaller numbers and gradually increase the complexity. There are numerous online resources, worksheets, and games to help you improve your multiplication skills. Understanding the underlying concept of repeated addition can also be helpful.
Q: What are some real-world applications of prime factorization?
A: Prime factorization is crucial in cryptography, the science of secure communication. Many encryption methods rely on the difficulty of factoring very large numbers into their prime factors.
Conclusion: The Power of a Simple Equation
While 2 x 3 x 5 seems like a simple equation, its significance goes far beyond a basic arithmetic problem. It demonstrates fundamental principles of multiplication, showcases the concept of prime factorization, and highlights the widespread applications of multiplication in various fields. Mastering the understanding and application of such fundamental principles is essential for success in mathematics and beyond. From everyday calculations to advanced mathematical concepts, the power of multiplication lies in its simplicity and its ability to unlock complex solutions. Understanding this seemingly simple equation is a cornerstone to a deeper understanding of mathematics and its role in our world. Its significance lies not only in the answer but in the journey of understanding the principles it represents.
Latest Posts
Latest Posts
-
1 5 16 In Mm
Sep 17, 2025
-
24 Millimeters To Inches
Sep 17, 2025
-
107 Kg To Pounds
Sep 17, 2025
-
Profession Starting With O
Sep 17, 2025
-
Blake Auguries Of Innocence
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 2x 3 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.