2x X 2 X
renascent
Sep 16, 2025 · 7 min read
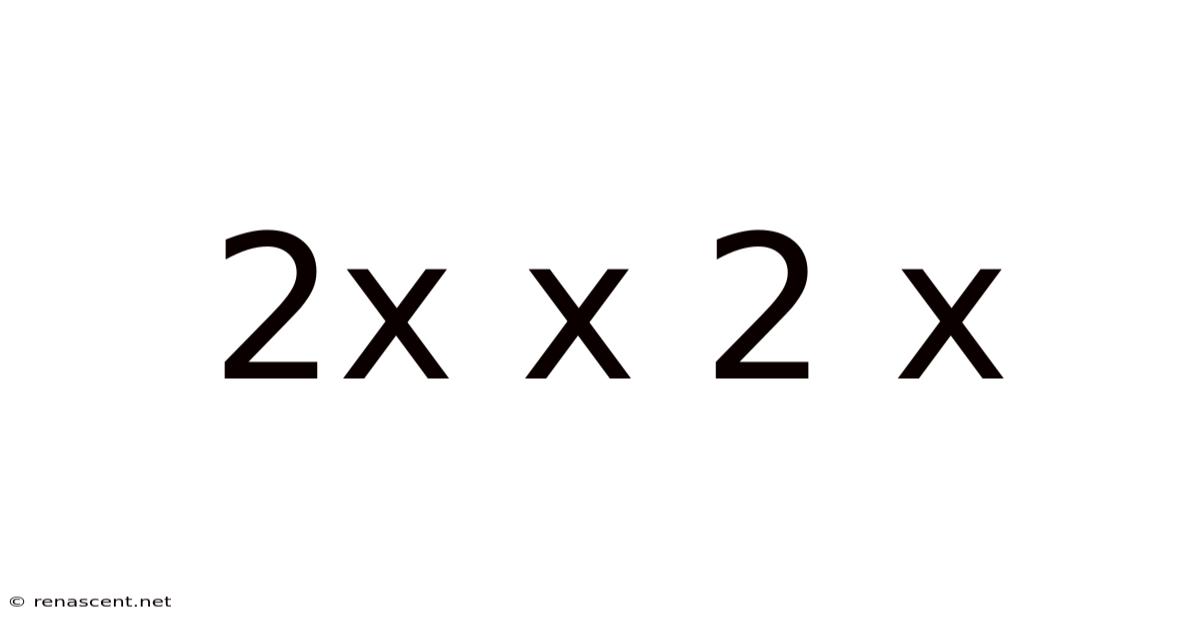
Table of Contents
Decoding 2 x 2 x 2: Exploring Cubes, Exponents, and Their Applications
This article delves into the seemingly simple mathematical expression "2 x 2 x 2," exploring its significance beyond basic multiplication. We'll unpack its representation in geometry as a cube, its connection to exponents, and its wide-ranging applications in various fields, from computer science to chemistry. Understanding this seemingly simple concept unlocks a deeper appreciation for fundamental mathematical principles and their practical implications. This exploration will be suitable for students, educators, and anyone curious about the power of fundamental math.
Introduction: More Than Just Multiplication
At first glance, 2 x 2 x 2 appears to be a straightforward multiplication problem with a solution of 8. While this is true, the expression holds far greater significance. It represents the volume of a cube with sides of length 2 units, a fundamental geometric shape. Moreover, it illustrates the concept of exponents, a crucial element in advanced mathematics and many scientific disciplines. This article will unpack each of these aspects, highlighting the connections between geometry, algebra, and real-world applications.
The Geometry of 2 x 2 x 2: The Cube
Geometrically, 2 x 2 x 2 represents a cube, a three-dimensional solid with six square faces, twelve edges, and eight vertices. Imagine a Rubik's Cube, a building block, or even a perfectly shaped sugar cube – these are all examples of cubes. The expression 2 x 2 x 2 calculates the volume of such a cube where each side (length, width, and height) measures 2 units. This means the cube contains 8 smaller unit cubes.
-
Visualizing the Cube: Try to visualize eight identical small cubes arranged to form a larger cube. This visual representation makes it easier to understand why 2 x 2 x 2 equals 8. Each dimension (length, width, height) contains two of these smaller cubes.
-
Beyond Unit Cubes: The principle applies regardless of the unit of measurement. If the sides of the cube are 2 centimeters, then the volume is 8 cubic centimeters (cm³). Similarly, if the sides are 2 meters, the volume is 8 cubic meters (m³). This demonstrates the scalability of the concept.
-
Surface Area: While the focus is on volume, it’s important to note that the cube also has a surface area. The surface area of a cube with side length 'a' is 6a². In our case (a=2), the surface area is 6 x 2² = 24 square units. This highlights the different geometric properties associated with a single mathematical concept.
Exponents and Exponential Growth: 2³
The expression 2 x 2 x 2 can also be written as 2³, using the notation of exponents. Here, '2' is the base and '3' is the exponent. The exponent indicates how many times the base is multiplied by itself. This concise notation is crucial for representing larger multiplications. For example, 2¹⁰ (2 to the power of 10) is far easier to write than 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2.
-
Exponential Growth: Exponents are fundamental to understanding exponential growth, a concept that describes situations where a quantity increases at a rate proportional to its current value. Examples of exponential growth include population growth, compound interest, and the spread of viruses. The 2 x 2 x 2 example, although simple, showcases the underlying principle.
-
Exponential Decay: Conversely, exponential decay describes situations where a quantity decreases at a rate proportional to its current value. Examples include radioactive decay and the cooling of objects. While not directly represented by 2 x 2 x 2, understanding exponents is crucial for grasping exponential decay as well.
-
Scientific Notation: Exponents are crucial in scientific notation, a way to represent very large or very small numbers concisely. For example, the speed of light is approximately 3 x 10⁸ meters per second. This utilizes an exponent (10⁸) to represent a large number efficiently.
Applications of 2 x 2 x 2 and Exponents
The seemingly simple 2 x 2 x 2 calculation and the broader concept of exponents find applications in diverse fields:
-
Computer Science: Binary code, the foundation of all digital computation, uses only two digits: 0 and 1. Exponents are crucial for representing and manipulating large binary numbers. The 2 x 2 x 2 concept directly relates to the number of possible states in a system with three binary bits (2³ = 8 states).
-
Chemistry: In chemistry, exponents are used in numerous calculations, including determining the concentration of solutions, calculating reaction rates, and understanding the behavior of gases (e.g., the ideal gas law).
-
Physics: Exponents appear in many physics equations, including those describing motion, forces, energy, and electromagnetism. Understanding exponents is essential for solving these equations and predicting physical phenomena.
-
Finance: Compound interest, a key concept in finance, is governed by exponential growth. Understanding exponents is critical for calculating the future value of investments and understanding the effects of interest rates.
-
Biology: Exponential growth is often observed in biological systems, such as bacterial growth and population dynamics. Understanding exponents helps model and predict these growth patterns.
-
Engineering: Many engineering designs involve calculations that utilize exponents, particularly when dealing with scaling, volume, and stress calculations.
Beyond 2 x 2 x 2: Generalizing the Concept
The principle of 2 x 2 x 2 can be generalized to other numbers and higher dimensions. For example:
-
3 x 3 x 3: This represents the volume of a cube with sides of length 3 units, resulting in a volume of 27 cubic units. This can also be written as 3³.
-
n x n x n: This represents the volume of a cube with sides of length 'n' units, which is equal to n³. This formula is applicable for any positive number 'n'.
-
Higher Dimensions: The concept can extend to higher dimensions. For example, a hypercube (a four-dimensional cube) would have a "hypervolume" calculated by multiplying four dimensions together.
-
Other Shapes: While the focus has been on cubes, the principle of multiplication to determine volume applies to various shapes, although the formulas become more complex.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between 2 x 2 x 2 and 2 + 2 + 2?
- A: 2 x 2 x 2 represents repeated multiplication (2 multiplied by itself three times), resulting in 8. 2 + 2 + 2 represents repeated addition, resulting in 6. These are fundamentally different operations.
-
Q: How is 2 x 2 x 2 related to binary numbers?
- A: In binary, numbers are represented using only 0 and 1. Three binary digits (bits) can represent 2³ = 8 different combinations (000, 001, 010, 011, 100, 101, 110, 111). This directly reflects the result of 2 x 2 x 2.
-
Q: Can 2 x 2 x 2 be used to calculate anything other than volume?
- A: Yes, while volume is a primary application, the underlying principle of repeated multiplication (exponentiation) is used extensively across numerous fields as described earlier.
-
Q: What is the significance of exponents in mathematics?
- A: Exponents provide a concise way to represent repeated multiplication, making complex calculations simpler and facilitating understanding of concepts like exponential growth and decay. They're fundamental to algebra, calculus, and many other advanced mathematical concepts.
Conclusion: The Enduring Power of a Simple Equation
The seemingly simple expression 2 x 2 x 2 holds a depth and breadth of meaning that extends far beyond basic arithmetic. Its connections to geometry, exponents, and various scientific fields showcase the interconnectedness of mathematical concepts and their widespread applications. Understanding this fundamental concept helps build a solid foundation for more advanced mathematical studies and provides a lens through which to view and understand the world around us. From the simple cube to complex scientific models, the power of 2 x 2 x 2, and the broader concept of exponents, is undeniable. It is a testament to the elegant simplicity and enduring power of fundamental mathematical principles.
Latest Posts
Latest Posts
-
150 Grams To Ounces
Sep 16, 2025
-
124 Pounds In Kilos
Sep 16, 2025
-
190 Pounds In Kilos
Sep 16, 2025
-
2 5 G To Mg
Sep 16, 2025
-
125 Kilograms To Pounds
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 2x X 2 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.