3 14 3 7
renascent
Sep 24, 2025 · 6 min read
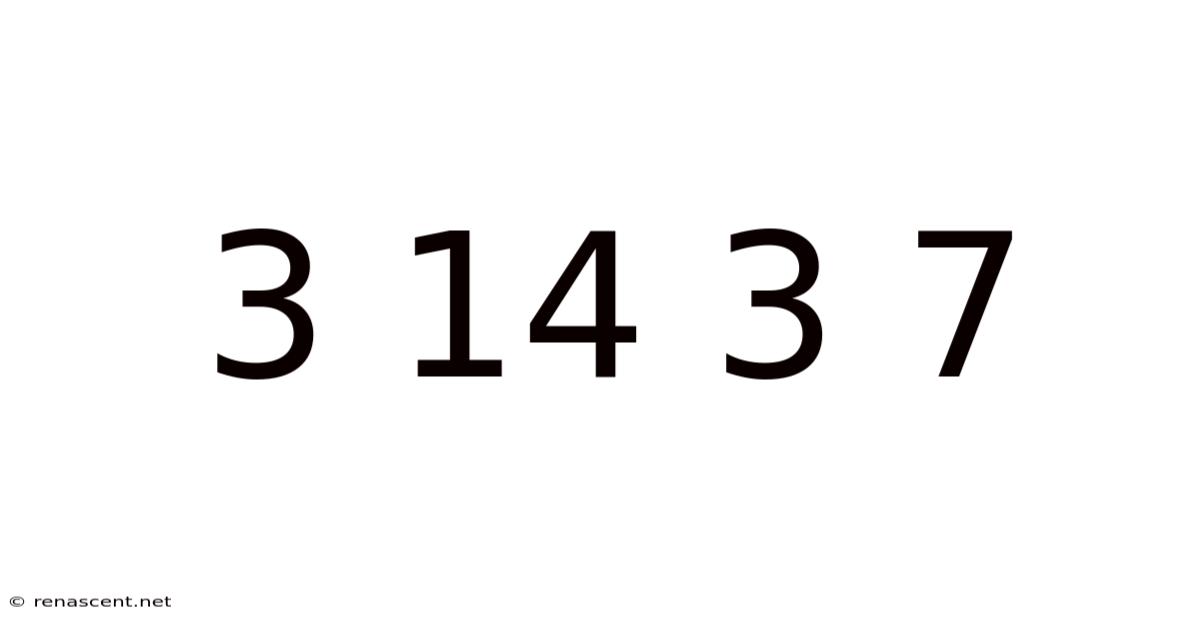
Table of Contents
Unlocking the Mysteries of 3 14 3 7: A Deep Dive into Pi and its Applications
The seemingly random sequence "3 14 3 7" immediately conjures an image for many: the mathematical constant Pi (π). This article delves deep into the fascinating world of Pi, exploring its history, its precise value, its mathematical significance, and its surprisingly wide range of applications across various fields. We'll move beyond the commonly known approximation of 3.14 and uncover the deeper mysteries behind this iconic number.
Introduction: The Endless Journey of Pi
Pi (π) is the ratio of a circle's circumference to its diameter. This means that regardless of the size of the circle, this ratio will always remain constant – approximately 3.14159. However, the key word here is approximately. Pi is an irrational number, meaning its decimal representation goes on forever without repeating. This seemingly simple concept has captivated mathematicians and scientists for millennia, driving advancements in mathematics, physics, and engineering. The sequence "3 14 3 7" represents a truncated version of Pi, highlighting its infinite nature and prompting us to explore its significance.
A Brief History: From Ancient Civilizations to Modern Computing
The understanding and calculation of Pi have evolved over centuries. Ancient civilizations, including the Babylonians and Egyptians, made early approximations of Pi, though their accuracy was limited by the tools and methods available at the time. The Babylonians used a value of approximately 3.125, while the Egyptians approximated it as 3.16. These early approximations, while crude by today's standards, represent significant milestones in the history of mathematics.
The Greek mathematician Archimedes (c. 287 – c. 212 BC) is credited with one of the first significant advancements in calculating Pi. He used the method of exhaustion, inscribing and circumscribing polygons around a circle to progressively narrow down the value of Pi. His calculated value, accurate to two decimal places, remained a benchmark for centuries.
The development of calculus in the 17th century revolutionized the calculation of Pi. Infinite series and other advanced mathematical techniques allowed mathematicians to compute Pi to an increasingly higher degree of accuracy. Isaac Newton and Gottfried Wilhelm Leibniz independently developed infinite series that could be used to calculate Pi, significantly advancing our understanding of this mathematical constant.
The advent of computers in the 20th century marked a new era in Pi calculation. Powerful computing capabilities allowed mathematicians to calculate Pi to trillions, and even quadrillions, of digits. This quest for ever-increasing precision is not merely an academic exercise; it serves as a testing ground for new algorithms and computer hardware. The computation of Pi pushes the boundaries of computational power and provides valuable insights into the efficiency and performance of modern computer systems.
The Mathematical Significance of Pi: Beyond the Circle
While Pi's definition is intrinsically linked to circles, its applications extend far beyond geometry. It appears in numerous mathematical formulas and equations across diverse fields. Here are some notable examples:
-
Trigonometry: Pi plays a crucial role in trigonometric functions such as sine, cosine, and tangent. These functions are fundamental to understanding periodic phenomena and are used extensively in physics and engineering.
-
Calculus: Pi appears in various calculus concepts, including integration and differentiation. Its presence in these fundamental mathematical tools highlights its pervasive influence on higher-level mathematical concepts.
-
Probability and Statistics: Pi unexpectedly appears in various probability distributions and statistical formulas. This highlights the interconnectedness of seemingly disparate mathematical branches.
-
Number Theory: Pi's infinite and non-repeating decimal expansion is a source of ongoing research in number theory, exploring its relationship with other irrational and transcendental numbers.
Applications of Pi: From Engineering to Cosmology
Pi's influence extends far beyond the realm of pure mathematics. Its applications span a remarkable range of disciplines:
-
Engineering and Architecture: Pi is essential in designing circular structures, calculating volumes of cylindrical objects, and determining the area of circular cross-sections. From bridges and buildings to pipes and gears, Pi is an integral part of engineering calculations.
-
Physics: Pi is ubiquitous in physics. It's found in equations describing wave motion, oscillations, and various physical phenomena involving circular or spherical symmetry. It plays a vital role in fields such as mechanics, electromagnetism, and quantum mechanics.
-
Computer Science: Pi is used in algorithms for generating random numbers, simulating physical processes, and developing graphical user interfaces (GUIs). The quest for more accurate calculations of Pi has also been a driving force in the development of more powerful algorithms and computer hardware.
-
Cosmology and Astronomy: Pi appears in equations that describe the geometry of the universe and the movements of celestial bodies. In astrophysics, it is integral to calculations involving gravitational forces, orbital mechanics, and the geometry of celestial objects.
Why Calculate Pi to Trillions of Digits?
The ongoing quest to calculate Pi to ever-increasing precision might seem unnecessary to the casual observer. However, this pursuit serves several crucial purposes:
-
Testing computational power: The calculation of Pi to a high number of digits serves as a benchmark for testing the capabilities of supercomputers and new algorithms. It helps identify potential bottlenecks and optimize computational processes.
-
Algorithm development: The pursuit of high-precision Pi calculations pushes the boundaries of algorithm design. New and more efficient algorithms are constantly being developed to achieve higher accuracy in shorter times.
-
Mathematical discovery: The study of Pi's digits can reveal hidden patterns and relationships, potentially leading to new mathematical discoveries. While no significant patterns have been found so far, the search continues.
-
Error analysis: The precision of Pi calculations is crucial in various applications where even small errors can have significant consequences. By calculating Pi to a high number of digits, engineers and scientists can minimize potential errors in their calculations.
Frequently Asked Questions (FAQ)
Q: Is Pi ever going to be fully calculated?
A: No. Pi is an irrational number, meaning its decimal representation continues infinitely without repeating. It's impossible to fully calculate it.
Q: What is the current record for the number of digits of Pi calculated?
A: The record for the number of calculated digits of Pi is constantly being updated. It involves trillions upon trillions of digits and is continuously being expanded.
Q: What is the practical use of knowing Pi to such a high degree of accuracy?
A: While most practical applications only require a few decimal places of Pi, calculating it to a high degree of accuracy is primarily used for testing computational power and developing efficient algorithms, rather than for direct practical application.
Q: Are there any patterns in the digits of Pi?
A: While no discernible patterns have yet been found in the digits of Pi, this remains an ongoing area of mathematical research. Its randomness is itself a subject of ongoing study.
Conclusion: The Enduring Legacy of Pi
The sequence "3 14 3 7" is more than just a numerical representation; it's a gateway to the fascinating world of Pi. From its humble beginnings as a ratio of a circle's circumference to its diameter, Pi has evolved into a cornerstone of mathematics and science. Its applications permeate various fields, from engineering and physics to computer science and cosmology. The ongoing quest to understand and calculate Pi demonstrates the enduring human fascination with mathematical mysteries and the relentless pursuit of knowledge. The seemingly simple sequence "3 14 3 7" ultimately represents a journey of discovery that continues to inspire and challenge mathematicians and scientists alike. The infinite nature of Pi serves as a reminder of the vastness and complexity of the mathematical universe, constantly urging us to explore, discover, and understand more.
Latest Posts
Latest Posts
-
Square Root Of 63
Sep 24, 2025
-
Graph Velocity Vs Time
Sep 24, 2025
-
Carbon Fiber Mass Density
Sep 24, 2025
-
670 Divided By 6
Sep 24, 2025
-
Little Shop Horrors Plant
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 3 14 3 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.