3 4 8 9
renascent
Sep 19, 2025 · 6 min read
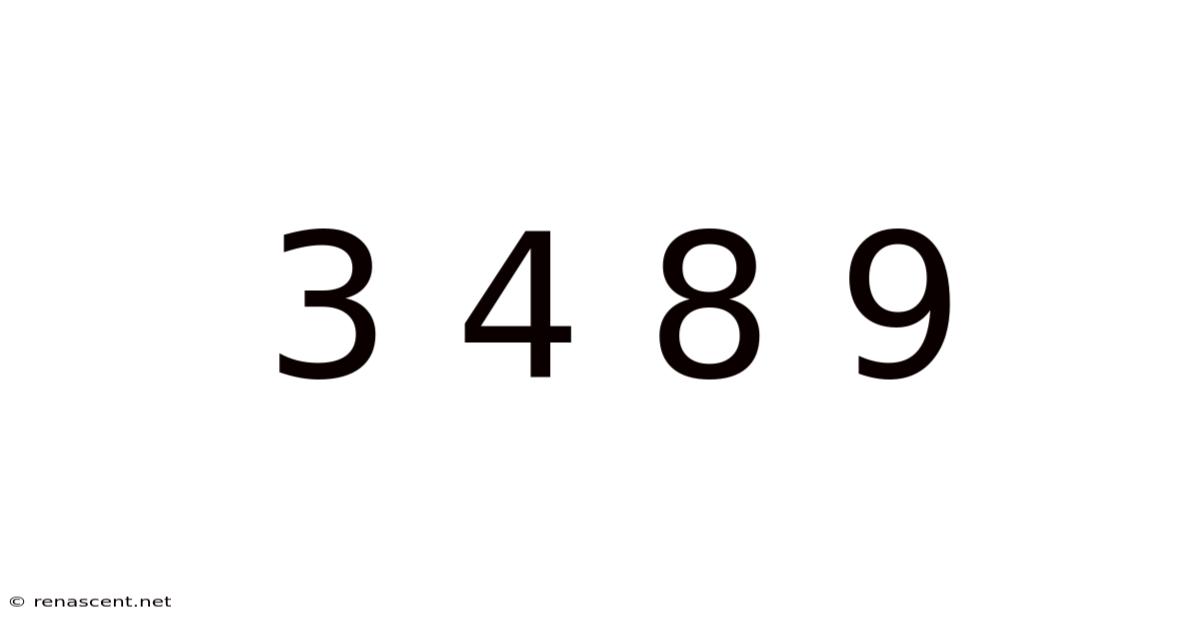
Table of Contents
The Enigmatic Sequence: Unraveling the Mysteries of 3, 4, 8, and 9
The seemingly simple sequence of numbers – 3, 4, 8, 9 – holds a surprising depth of mathematical intrigue and interconnectedness. While initially appearing random, a closer examination reveals fascinating patterns, relationships, and applications across various mathematical fields. This article delves into the properties of these four numbers, exploring their individual characteristics, their combined relationships, and their surprising appearances in diverse mathematical contexts, from simple arithmetic to more complex concepts. This exploration aims to reveal not only the "what" but also the "why" behind this captivating numerical quartet.
I. Individual Number Properties: A Closer Look
Before examining the relationships between 3, 4, 8, and 9, let's explore the individual characteristics of each number. Understanding their individual properties lays the groundwork for appreciating their intertwined nature.
A. The Number 3: Three is the first odd prime number after 2, making it a foundational element in number theory. It's also the smallest odd number and possesses unique divisibility properties. It’s frequently associated with concepts of trinity and wholeness across various cultures and belief systems. In geometry, it's the minimum number of sides needed to form a polygon (a triangle).
B. The Number 4: Four is the first composite number (a positive integer that has at least one divisor other than 1 and itself). It's also a perfect square (2 x 2 = 4), and represents stability and completeness in many contexts. Geometrically, it’s the number of sides in a square and the number of vertices in a tetrahedron. It plays a crucial role in various mathematical structures, including four-dimensional spaces.
C. The Number 8: Eight is a highly composite number, meaning it has a large number of divisors relative to its size. It's also a power of 2 (2³ = 8), which makes it significant in binary systems and computer science. In some cultures, eight is associated with prosperity and infinity. The geometry of the octahedron, an eight-faced polyhedron, also highlights its importance.
D. The Number 9: Nine is the largest single-digit number. It’s a composite number, and it exhibits interesting properties related to divisibility. Notably, the sum of the digits of any multiple of 9 will always eventually reduce to 9 (e.g., 27 -> 2 + 7 = 9; 108 -> 1 + 0 + 8 = 9). This is a fundamental property used in divisibility rules. In geometry, nine points define a unique conic section.
II. Interrelationships Within the Sequence: Unveiling the Patterns
The true fascination with the sequence 3, 4, 8, 9 emerges when we analyze the relationships between the numbers. Several intriguing connections emerge, highlighting the non-random nature of this seemingly arbitrary progression.
A. Arithmetic Relationships: While no simple arithmetic progression exists (like adding a constant value), there are interesting patterns observable through differences:
- The difference between 4 and 3 is 1.
- The difference between 8 and 4 is 4.
- The difference between 9 and 8 is 1.
This pattern of differences (1, 4, 1) is itself intriguing, although not immediately explainable by a simple formula.
B. Geometric Relationships: Examining geometric progressions, we find no straightforward relationship either. However, considering powers of 2, we find 8 is 2 cubed, while 4 is 2 squared. This suggests a potential link to exponential growth or power series.
C. Number Theory Connections: Analyzing divisibility, prime factorization, and other number theory concepts, we find subtle links. For instance, the prime factorization of 8 (2 x 2 x 2) and its relationship to the perfect square 4 (2 x 2) reveals a connection to powers of 2. The fact that 9’s digit sum always reduces to 9 provides another intriguing number-theoretic property.
III. Appearances in Mathematical Contexts: Beyond the Obvious
The numbers 3, 4, 8, and 9 appear unexpectedly in diverse areas of mathematics, enriching their significance beyond their initial presentation.
A. Geometry: As previously mentioned, these numbers feature prominently in geometric shapes and polyhedra. Three sides form a triangle, four sides a square, and eight and nine appear in more complex polyhedra and geometric configurations.
B. Number Theory: The number 9's divisibility rule is a fundamental concept in elementary number theory. The prime factorization of 8 highlights its relevance in modular arithmetic and other advanced number theory problems.
C. Algebra: These numbers can appear in algebraic equations and formulas, often as coefficients or exponents. Their specific roles will depend on the nature of the equation and the mathematical context.
D. Combinatorics: The numbers can appear in combinatorial problems, where counting arrangements or possibilities is central. For instance, 3, 4, 8, and 9 might represent different numbers of ways to arrange items or make selections.
E. Computer Science: The number 8, being a power of 2, is fundamental to binary systems, crucial in computer architecture and data representation.
IV. Expanding the Exploration: Further Research Avenues
The analysis presented above only scratches the surface of the mathematical depths associated with the sequence 3, 4, 8, 9. Several avenues of further exploration exist for interested mathematicians and number enthusiasts:
- Advanced Number Theory: Investigating the appearance of these numbers in Diophantine equations, modular arithmetic, or other advanced number theory concepts could reveal deeper connections.
- Fractals and Chaos Theory: Exploring the role of these numbers in iterative processes or fractal generation might reveal unexpected patterns.
- Abstract Algebra: Investigating the presence of these numbers in group theory or ring theory could illuminate hidden relationships.
- Mathematical Modeling: Utilizing these numbers as parameters in various mathematical models (e.g., population growth models, physical simulations) might reveal how these numbers influence model behavior.
V. Conclusion: The Enduring Enigma
The seemingly simple sequence 3, 4, 8, and 9, upon closer examination, reveals a rich tapestry of interconnectedness within the field of mathematics. While the sequence itself doesn't conform to readily apparent arithmetic or geometric progressions, the individual characteristics of each number, along with their subtle yet fascinating interrelationships, highlight their diverse applications and significance across various mathematical disciplines. Further research into the deeper mathematical structures that involve these numbers promises to unveil even more profound insights into their underlying patterns and implications. The enduring enigma of 3, 4, 8, and 9 serves as a testament to the ever-evolving and endlessly fascinating world of numbers.
VI. Frequently Asked Questions (FAQ)
Q: Is there a specific formula that generates the sequence 3, 4, 8, 9?
A: No simple, readily apparent formula generates this specific sequence. While patterns exist between the numbers (differences, relationships to powers of 2), a definitive formula remains elusive.
Q: Are these numbers significant in any specific cultural contexts?
A: While not universally significant in all cultures, the individual numbers (3, 4, 8, 9) hold symbolic meaning in various belief systems and cultural traditions. For example, the number 3 is often associated with the Trinity, while 8 represents prosperity in some cultures.
Q: Could this sequence be part of a larger, undiscovered mathematical sequence?
A: It's entirely possible. The sequence might be a segment of a larger, more complex pattern waiting to be discovered through further mathematical investigation.
Q: What are some practical applications of understanding the properties of this sequence?
A: While no immediate, direct practical application is readily apparent, understanding the underlying mathematical principles (divisibility rules, number theory concepts, relationships between powers of 2) has broad implications across various fields.
Q: Why is studying this sequence important?
A: Studying this sequence, even if seemingly arbitrary, fosters a deeper appreciation for the interconnectedness of mathematical concepts. It demonstrates the value of exploring seemingly simple sequences to discover hidden patterns and deeper relationships within mathematics. This process fosters critical thinking and problem-solving skills.
Latest Posts
Latest Posts
-
Day Night World Map
Sep 19, 2025
-
150 Celsius En Fahrenheit
Sep 19, 2025
-
245 Pounds To Kg
Sep 19, 2025
-
2 X 0 4
Sep 19, 2025
-
137 Minutes In Hours
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 3 4 8 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.