3 Percent Of 68
renascent
Sep 21, 2025 · 5 min read
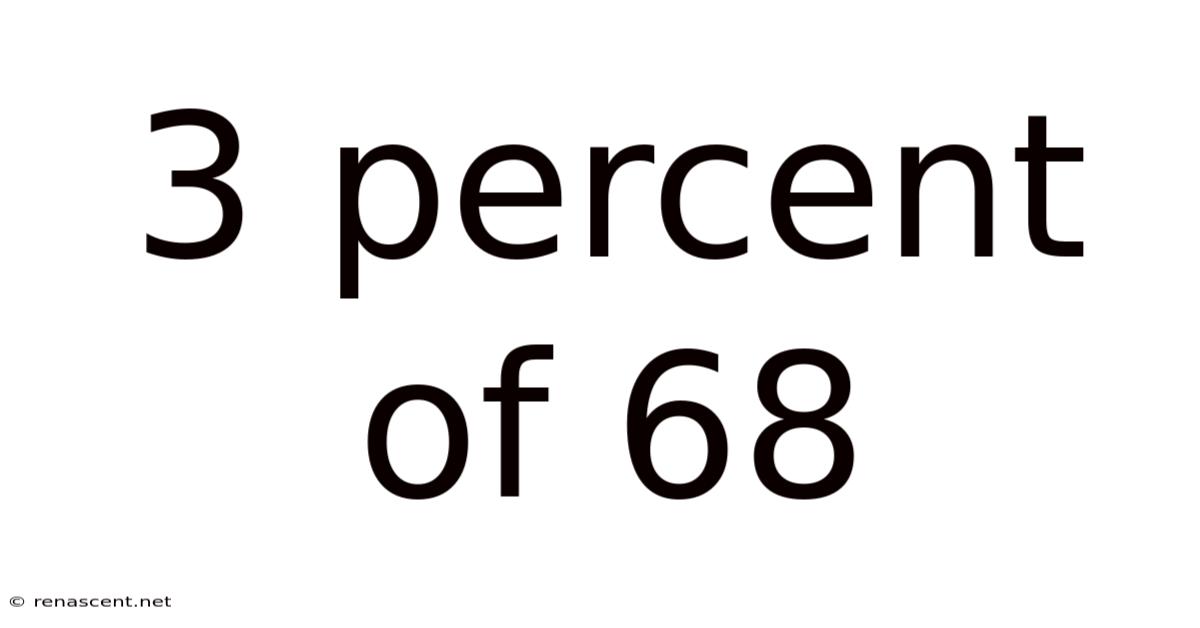
Table of Contents
Decoding 3 Percent of 68: A Deep Dive into Percentages and Their Applications
Finding 3 percent of 68 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding how to calculate percentages, and more importantly, the underlying concepts, opens doors to a vast world of applications in various fields, from finance and statistics to everyday life decisions. This article will guide you through calculating 3% of 68, explore the different methods, delve into the theoretical underpinnings, and discuss practical scenarios where such calculations are essential. We'll also tackle some frequently asked questions and explore further applications of percentage calculations.
Understanding Percentages: The Basics
Before we dive into calculating 3% of 68, let's refresh our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." So, 3% means 3 out of 100, or 3/100. This can be expressed as a decimal (0.03) or a fraction (3/100). Understanding these different representations is crucial for performing percentage calculations efficiently.
Method 1: Using the Decimal Equivalent
The most straightforward method for calculating 3% of 68 is to convert the percentage to its decimal equivalent and then multiply it by the number.
-
Convert the percentage to a decimal: 3% is equal to 0.03 (simply divide 3 by 100).
-
Multiply the decimal by the number: 0.03 * 68 = 2.04
Therefore, 3% of 68 is 2.04.
This method is quick, efficient, and easily adaptable to any percentage calculation. It's the preferred method for most practical applications due to its simplicity and speed, especially when using calculators.
Method 2: Using the Fraction Equivalent
Alternatively, we can use the fraction equivalent of 3%.
-
Express the percentage as a fraction: 3% is equal to 3/100.
-
Multiply the fraction by the number: (3/100) * 68 = 204/100
-
Simplify the fraction: 204/100 can be simplified to 2.04 by dividing both the numerator and the denominator by 100.
Again, we arrive at the answer: 3% of 68 is 2.04. While this method is conceptually sound, it can be slightly more time-consuming, especially for larger numbers or more complex percentages.
Method 3: Proportion Method
This method is particularly useful for understanding the underlying concept of percentages and for solving problems where the percentage is unknown.
We can set up a proportion:
3/100 = x/68
where 'x' represents the unknown value (3% of 68).
To solve for x, we cross-multiply:
100x = 3 * 68 100x = 204 x = 204/100 x = 2.04
This method reinforces the idea that a percentage represents a ratio, making it a valuable tool for understanding the relationship between percentages and the whole.
The Importance of Understanding Percentage Calculations
The ability to calculate percentages is a fundamental skill applicable across numerous fields:
-
Finance: Calculating interest rates, discounts, tax amounts, profit margins, and investment returns all rely heavily on percentage calculations. Understanding these calculations is vital for making informed financial decisions.
-
Statistics: Percentages are ubiquitous in statistical analysis, representing proportions, probabilities, and rates of change. Analyzing data, interpreting surveys, and understanding statistical significance all involve working with percentages.
-
Science: Many scientific measurements and experiments involve percentages, such as concentration of solutions, error rates, and growth rates.
-
Everyday Life: We encounter percentages daily – from sales discounts in stores to calculating tips in restaurants, understanding percentages empowers us to make informed decisions and manage our finances effectively.
Beyond the Basics: More Complex Percentage Problems
While calculating 3% of 68 is relatively simple, the principles involved extend to more complex scenarios. Consider these examples:
-
Calculating Percentage Increase/Decrease: Suppose a product's price increases by 15%. To calculate the new price, you'd first find 15% of the original price and then add it to the original price.
-
Finding the Original Value: If you know the final value after a percentage increase or decrease, you can work backward to find the original value using algebraic methods.
-
Compound Interest: This involves calculating interest not only on the principal amount but also on the accumulated interest. Compound interest calculations require a more sophisticated understanding of percentage calculations.
Frequently Asked Questions (FAQ)
Q: What if I need to calculate a percentage greater than 100%?
A: This is perfectly possible and represents a value greater than the original whole. For example, 150% of 68 would be calculated as 1.5 * 68 = 102.
Q: How can I calculate percentages without a calculator?
A: While a calculator makes the process faster, you can perform manual calculations using the fraction or proportion method. For simple percentages like 10%, 25%, or 50%, mental math techniques can be used.
Q: What are some common mistakes to avoid when calculating percentages?
A: A common mistake is forgetting to convert the percentage to a decimal or fraction before multiplying. Another mistake is incorrectly using the percentage increase/decrease formula.
Conclusion: Mastering Percentages - A Lifelong Skill
Calculating 3% of 68, while seemingly basic, serves as a gateway to understanding the broader concept of percentages and their pervasive role in numerous aspects of life. Mastering percentage calculations isn't just about solving arithmetic problems; it’s about developing a crucial skillset that empowers you to analyze data, make informed decisions, and navigate the quantitative world around you effectively. From managing your personal finances to excelling in academic and professional pursuits, a strong grasp of percentages is a valuable asset that will serve you well throughout your life. The methods outlined in this article provide a solid foundation for tackling various percentage problems, no matter how complex they may seem. Remember to practice regularly and explore more advanced applications to further solidify your understanding.
Latest Posts
Latest Posts
-
Foods With One Ingredient
Sep 21, 2025
-
Dali Swans And Elephants
Sep 21, 2025
-
Vividly Descriptive Crossword Clue
Sep 21, 2025
-
Stardew Miner Or Geologist
Sep 21, 2025
-
45 Dived By 3
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 3 Percent Of 68 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.