3 X 1 2
renascent
Sep 21, 2025 · 6 min read
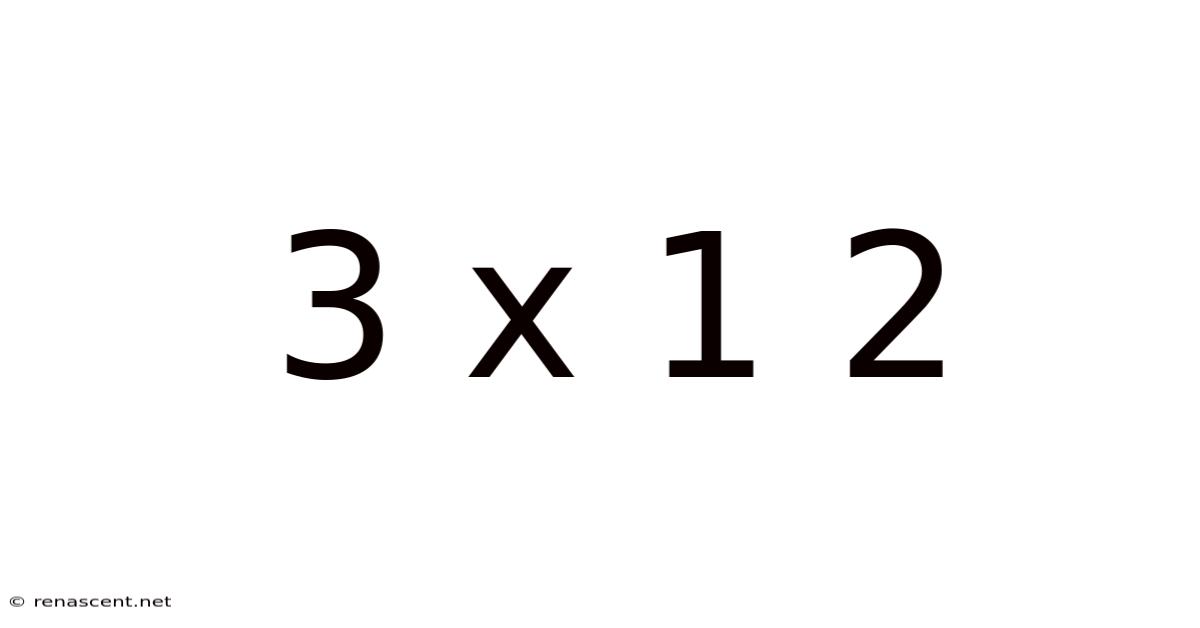
Table of Contents
Decoding 3 x 1 2: Exploring the Multifaceted Applications of a Simple Expression
The seemingly simple mathematical expression "3 x 1 2" might appear straightforward at first glance. However, a deeper dive reveals its multifaceted nature and surprising applications across various fields, from basic arithmetic to advanced concepts in computer science and cryptography. This article aims to demystify this expression, exploring its different interpretations and showcasing its relevance in diverse contexts. Understanding 3 x 1 2 isn't just about solving a simple multiplication; it's about grasping fundamental principles that underpin more complex mathematical and computational operations.
Understanding the Basics: Order of Operations (PEMDAS/BODMAS)
Before we delve into advanced applications, let's clarify the fundamental issue: the order of operations. The expression "3 x 1 2" is ambiguous without specifying the order in which the operations should be performed. Different mathematical conventions dictate the order of operations, usually summarized by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). Both acronyms represent the same hierarchy of operations.
Following the standard order of operations (PEMDAS/BODMAS), multiplication takes precedence over addition. Therefore, the correct interpretation of "3 x 1 2" is:
3 x (1 + 2) = 3 x 3 = 9
This clarifies the ambiguity and provides the unambiguous solution. However, the lack of parentheses highlights the importance of precise notation in mathematical expressions. Ambiguity can lead to incorrect results, especially in more complex equations.
Beyond Basic Arithmetic: Applications in Computer Science
The seemingly simple expression "3 x 1 2" finds practical application in computer science, particularly in areas involving binary operations, bit manipulation, and data representation. Let's explore some examples:
-
Bitwise Operations: In programming, numbers are often represented in binary form (using only 0s and 1s). Bitwise operations work directly on individual bits of a number. While "3 x 1 2" doesn't directly involve bitwise operations in its standard decimal form, the principles behind it (multiplication and addition) are fundamental to many bitwise algorithms. For example, calculating the size of a data structure in bytes often involves multiplication.
-
Array Indexing and Manipulation: Consider an array (a data structure that stores a collection of elements) with a size of 3 x 12 elements. This would equate to a total of 36 elements. The expression "3 x 1 2" directly reflects the calculation needed to determine the total number of elements. This is crucial for tasks like memory allocation and efficient data access.
-
Looping and Iteration: Imagine a nested loop structure in programming where the outer loop iterates 3 times, and the inner loop iterates 12 times. The total number of iterations performed by the code can be represented using "3 x 1 2" = 36. Understanding this calculation is critical for optimizing code performance and predicting execution time.
Extending the Concept: Matrices and Linear Algebra
The expression 3 x 1 2 can be conceptually extended into the realm of linear algebra, specifically when dealing with matrices and vectors. While not a direct representation, the underlying multiplication and addition operations are essential to matrix operations.
Consider a 3x1 matrix (a matrix with 3 rows and 1 column) and a 1x2 matrix (a matrix with 1 row and 2 columns). Matrix multiplication involves a specific procedure where corresponding elements are multiplied and summed. Although the direct multiplication "3 x 1 2" isn't applicable in this context without appropriate matrix dimensions, the core concepts of multiplication and summation are fundamental to matrix operations.
Advanced Applications: Cryptography and Security
Although less direct, the principles underlying "3 x 1 2" are fundamental to more complex mathematical operations used in cryptography and cybersecurity. Cryptography relies heavily on modular arithmetic, prime numbers, and other advanced mathematical concepts. While the expression itself doesn't directly appear in cryptographic algorithms, the understanding of basic arithmetic operations forms the groundwork for comprehending these more complex algorithms.
For example, many cryptographic systems utilize modular arithmetic. Modular arithmetic involves performing arithmetic operations within a specific range (modulo). The basic principles of addition and multiplication learned through understanding "3 x 1 2" are essential building blocks for understanding modular arithmetic.
The Significance of Parentheses and Order of Operations
The ambiguity inherent in "3 x 1 2" without parentheses underscores the critical importance of precise mathematical notation. The order of operations is not arbitrary; it ensures consistency and avoids ambiguity. In more complex equations, neglecting the order of operations can lead to catastrophic errors, especially in fields like engineering, physics, and computer science. The use of parentheses provides clarity and removes any potential for misinterpretation.
Expanding the Scope: Variations and Extensions
While the original expression focuses on simple integers, we can expand the scope to include:
-
Fractions and Decimals: The expression can be modified to include fractions and decimals. For instance, 3 x (1.5 + 2.5) = 12, or 3 x (1/2 + 2) = 3 x (5/2) = 15/2 = 7.5. These variations demonstrate the applicability of the underlying principles to a wider range of numerical values.
-
Algebraic Expressions: The expression can be extended to include variables. For instance, 3x(a + b), where 'a' and 'b' represent unknown values. This showcases the scalability of the underlying concepts to algebraic manipulations and equation solving.
-
Functions and Calculus: The principles of addition and multiplication are fundamental to calculus, the study of change. Functions and their derivatives rely heavily on these operations.
Frequently Asked Questions (FAQ)
Q: What is the most common interpretation of "3 x 1 2"?
A: Following the order of operations (PEMDAS/BODMAS), the most common interpretation is 3 x (1 + 2) = 9.
Q: Why are parentheses so important in mathematical expressions?
A: Parentheses ensure clarity and remove ambiguity by specifying the order in which operations should be performed. Without parentheses, different interpretations are possible, leading to incorrect results.
Q: Can "3 x 1 2" be interpreted differently depending on the context?
A: Yes, while the standard interpretation is 9, the context might influence the interpretation, especially in programming or specialized mathematical fields where unconventional notations might be used. However, proper notation should always clarify this ambiguity.
Q: How does understanding "3 x 1 2" help in more advanced mathematical concepts?
A: Understanding the underlying principles of addition and multiplication embodied in "3 x 1 2" forms a crucial foundation for grasping more advanced mathematical concepts like matrix operations, modular arithmetic, and calculus.
Q: Are there any real-world examples where this expression is directly used?
A: While "3 x 1 2" might not be explicitly written in many real-world scenarios, the principles of multiplication and addition it represents are fundamental to numerous calculations in various fields, such as determining the total number of items in a grid, calculating area, and various aspects of computer programming.
Conclusion: More Than Meets the Eye
The seemingly simple expression "3 x 1 2" is more than just a basic arithmetic problem. It serves as a gateway to understanding fundamental mathematical principles applicable across numerous disciplines. From basic arithmetic to advanced concepts in computer science and cryptography, the underlying principles of multiplication, addition, and the importance of order of operations are crucial for problem-solving and numerical analysis. By understanding the nuances of this expression, we gain valuable insights into the elegance and power of mathematics and its profound impact on our world. The seemingly simple equation reveals a depth of understanding far exceeding its initial appearance. It acts as a microcosm representing the vast and interconnected landscape of mathematics and its applications.
Latest Posts
Latest Posts
-
13 Hours Ago Now
Sep 21, 2025
-
112 Mile In Km
Sep 21, 2025
-
Treaty Of Versailles Cartoon
Sep 21, 2025
-
Themes In The Outsiders
Sep 21, 2025
-
Advantages Of The Network
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 3 X 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.