3 X 2 7
renascent
Sep 18, 2025 · 6 min read
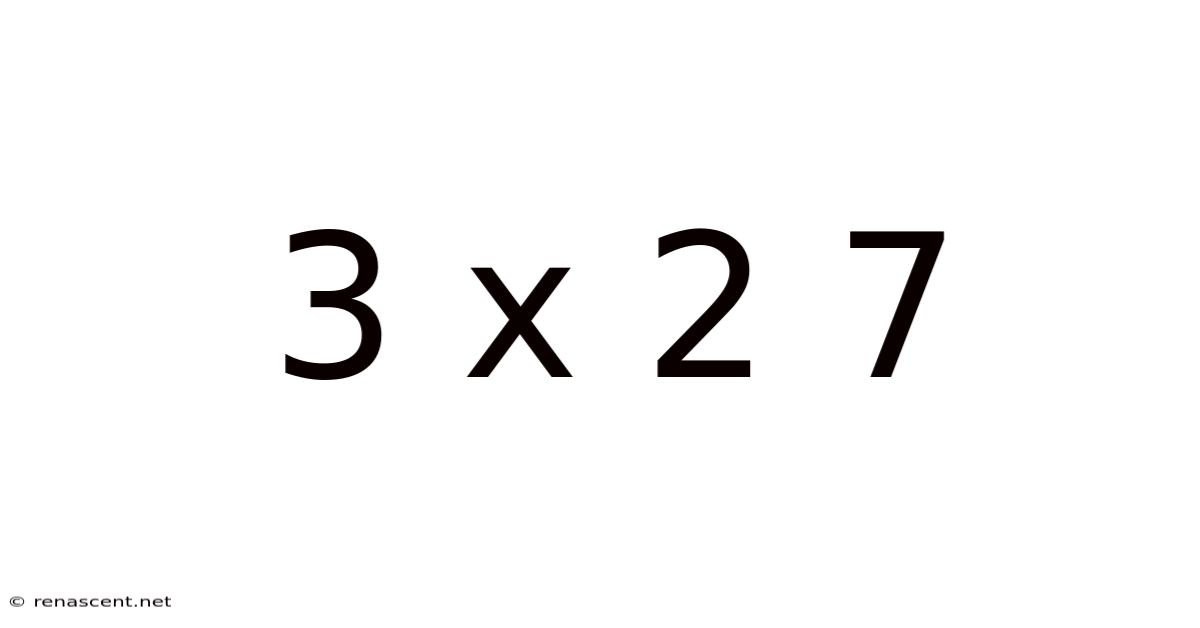
Table of Contents
Decoding the Enigma: A Deep Dive into "3 x 2 = 7"
This seemingly simple equation, "3 x 2 = 7," is fundamentally incorrect within the standard mathematical framework. However, exploring its inherent falsehood opens doors to fascinating discussions about mathematical axioms, alternative number systems, and even the nature of truth and representation itself. This article will delve into the various perspectives surrounding this equation, explaining why it's wrong, exploring potential contexts where it might hold a symbolic meaning, and finally, examining the broader implications for understanding mathematical systems.
Introduction: Why 3 x 2 ≠ 7 in Standard Arithmetic
At its core, the statement "3 x 2 = 7" violates the fundamental principles of arithmetic. Multiplication, at its simplest, represents repeated addition. 3 x 2 means adding three two times: 2 + 2 + 2 = 6. This is a universally accepted truth within the standard decimal number system. The equation is incorrect because it asserts a false equivalence – 6 is not equal to 7. This discrepancy stems from a misunderstanding or deliberate misrepresentation of the basic arithmetic operation.
Understanding Multiplication: A Foundation of Arithmetic
Before we delve into the intricacies of alternative systems, it's crucial to solidify our understanding of multiplication within the standard mathematical framework. Multiplication is a binary operation, meaning it takes two inputs (operands) and produces one output (result). These inputs are usually numbers. The operation itself signifies repeated addition. For example:
- 2 x 3: This means adding 2 three times: 2 + 2 + 2 = 6
- 5 x 4: This means adding 5 four times: 5 + 5 + 5 + 5 = 20
- 1 x 10: This means adding 1 ten times: 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 10
The commutative property of multiplication states that the order of operands doesn't change the result (a x b = b x a). This consistency is fundamental to the predictability and reliability of arithmetic. The associative property allows us to group operands without affecting the outcome ((a x b) x c = a x (b x c)). These properties are cornerstones of standard arithmetic, and their violation leads to inconsistent results.
Exploring Potential Interpretations Beyond Standard Arithmetic
While "3 x 2 = 7" is undeniably false in standard arithmetic, the phrase can still be explored within alternative frameworks. Let's examine some of these:
-
Contextual Interpretation: Could "3 x 2 = 7" represent a symbolic statement rather than a strict mathematical equation? Perhaps in a specific narrative or code, this might function as an identifier or placeholder. For instance, it could be a fictional unit of measurement within a fantasy story, representing "3 units of X combined with 2 units of Y to yield 7 units of Z," where the units are not directly related to standard numerical values.
-
Modular Arithmetic: Modular arithmetic involves working with remainders after division. In modulo 7 arithmetic, numbers "wrap around" after reaching 7. While 3 x 2 equals 6 in standard arithmetic, in modulo 7, 6 is equivalent to -1. There is no straightforward interpretation that would make "3 x 2 = 7" true within a standard modulo system.
-
Errors in Measurement or Approximation: In real-world scenarios involving measurements, slight errors are inevitable. Perhaps the equation arose from an approximation where values are rounded up or down. For instance, if we are dealing with quantities that cannot be precisely measured, say, the number of grains of sand, we might encounter approximations leading to such discrepancies. However, this is not a mathematical truth; it's a consequence of the limitations of measurement.
-
Abstract Algebraic Structures: Advanced mathematical fields deal with abstract algebraic structures that go beyond the standard number system. These structures, like groups, rings, and fields, define operations with specific rules that may not resemble standard addition or multiplication. It's theoretically possible to construct an algebraic structure where an operation analogous to multiplication yields this result, but this structure would be significantly different from what is commonly understood as arithmetic.
The Importance of Axioms and Defining Mathematical Systems
The falsehood of "3 x 2 = 7" highlights the importance of axioms—the foundational statements that define a mathematical system. These axioms are accepted as true without proof and serve as the basis for deriving all other theorems and results within that system. Standard arithmetic rests on a set of well-defined axioms, including the commutative and associative properties of addition and multiplication, the distributive property, and the existence of additive and multiplicative identities (0 and 1, respectively). These axioms ensure consistency and predictability. Any deviation from these axioms leads to a different system, potentially with entirely different properties.
Mathematical Consistency and the Search for Truth
The consistency of a mathematical system is paramount. It ensures that the system doesn't lead to contradictions, which would render it useless. A system where "3 x 2 = 7" and "3 x 2 = 6" both hold true would be fundamentally inconsistent. This inconsistency renders the system illogical and impractical. The search for truth in mathematics hinges on creating consistent and robust systems that allow us to build upon fundamental truths to explore increasingly complex concepts.
The Role of Notation and Representation
The simple equation "3 x 2 = 7" also touches on the importance of notation. The symbols "3," "2," "7," "x," and "=" each represent specific concepts. The notation used needs to be consistent and understood by everyone within the same mathematical framework. This is crucial for communication and understanding. A change in notation could lead to misinterpretations, further highlighting the importance of precise and universally understood symbolic representations.
FAQ: Addressing Common Questions
Q: Could there be any scenario where 3 x 2 = 7 is considered correct?
A: Within the framework of standard arithmetic, no. However, as explained above, in fictional contexts or within highly abstract algebraic structures, the statement might be used symbolically, but it would not hold true mathematically.
Q: What if we use a different base number system?
A: Changing the base (e.g., from base 10 to base 2 or base 16) alters the representation of numbers, but it does not change the underlying mathematical operations. The fundamental principles of multiplication will remain consistent. 3 x 2 will always equal 6, regardless of the base system used to represent the numbers.
Q: Is there any practical application of exploring statements like this?
A: Exploring seemingly false statements like "3 x 2 = 7" helps us understand the foundational principles of mathematics. It reinforces the importance of axioms, consistency, and the role of notation in the construction and interpretation of mathematical systems. It also demonstrates the limitations of applying standard arithmetic in non-standard contexts and encourages critical thinking about mathematical truths.
Conclusion: The enduring value of mathematical accuracy
The statement "3 x 2 = 7" is unequivocally false within the realm of standard mathematics. This falsity is not arbitrary; it stems from the fundamental axioms and consistent rules that govern arithmetic. Exploring this seemingly simple equation, however, provides a valuable opportunity to delve into the underlying principles of mathematics, highlighting the importance of consistent systems, the role of notation, and the ever-present need for accurate mathematical reasoning. It encourages a deeper appreciation for the elegance and precision at the heart of the mathematical world. The pursuit of mathematical truth relies on rigorously defined rules and logical consistency; straying from these principles leads to inconsistencies and a breakdown of the system's integrity. Therefore, while "3 x 2 = 7" might spark curiosity, it ultimately serves as a reminder of the bedrock principles that underpin the structure and beauty of mathematics.
Latest Posts
Latest Posts
-
26 2 Miles In Kilometres
Sep 18, 2025
-
Rhyming Word Of Warm
Sep 18, 2025
-
Weight Of A Orange
Sep 18, 2025
-
Example Of A Procedure
Sep 18, 2025
-
80 Usd In Aud
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 3 X 2 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.