30 Divided By 12
renascent
Sep 22, 2025 · 6 min read
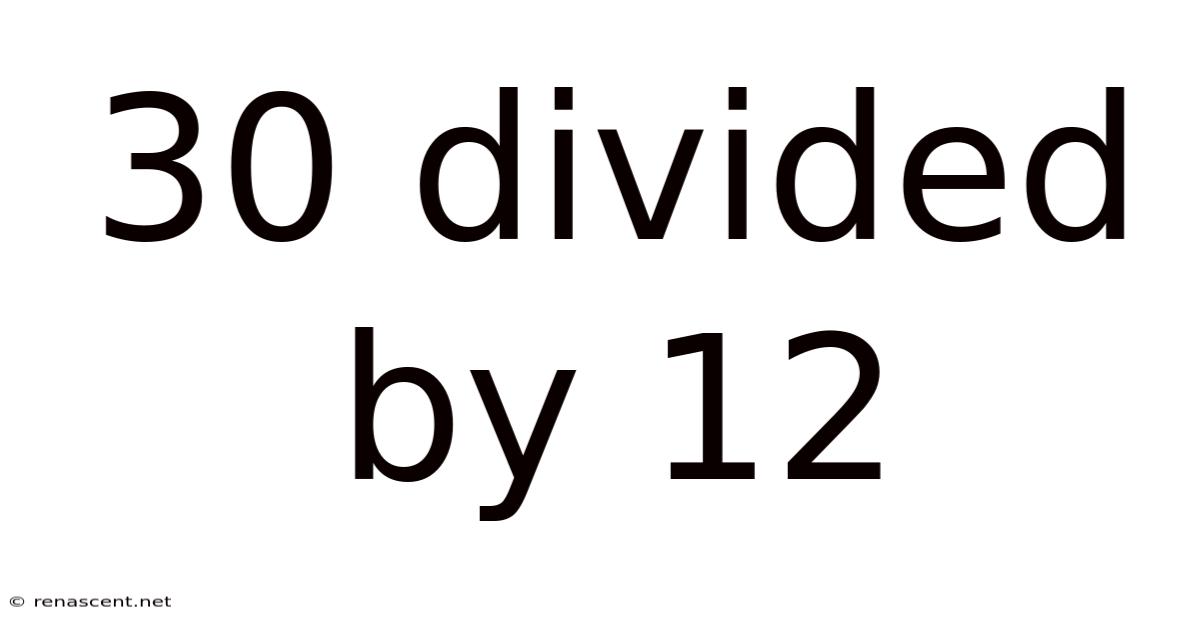
Table of Contents
30 Divided by 12: A Deep Dive into Division and its Applications
Introduction:
This article explores the seemingly simple calculation of 30 divided by 12, going far beyond a simple answer. We'll delve into the underlying principles of division, explore different methods for solving this problem, discuss its practical applications, and address common misconceptions. Understanding division is fundamental to various aspects of mathematics and everyday life, and this in-depth analysis will provide a solid foundation for grasping more complex mathematical concepts. We will also examine the concept of remainders and their significance, and consider how this specific division problem might be represented visually. This comprehensive guide is perfect for anyone looking to strengthen their understanding of arithmetic, particularly division, and its practical relevance.
Understanding Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts or groups. In the context of 30 divided by 12 (written as 30 ÷ 12, 30/12, or 12)30), we're asking: "How many times does 12 fit into 30?"
There are several ways to interpret division:
-
Partitioning: Dividing 30 into 12 equal groups. This helps visualize the problem as splitting 30 objects into 12 containers, with an equal number of objects in each.
-
Measurement: Determining how many times 12 fits into 30. This is like measuring a 30-unit length using a 12-unit ruler. How many times do you need to use the ruler to measure the entire length?
Both interpretations lead to the same answer, but the visualization differs, impacting the approach to solving the problem.
Calculating 30 Divided by 12
The most straightforward way to calculate 30 ÷ 12 is through long division.
Long Division Method:
-
Set up the problem: Write the dividend (30) inside the division bracket and the divisor (12) outside.
12 | 30 -
Determine the quotient: Ask yourself, "How many times does 12 go into 30?" It goes in twice (2 x 12 = 24). Write the "2" above the 0 in 30.
2 12 | 30 -
Multiply and subtract: Multiply the quotient (2) by the divisor (12), resulting in 24. Subtract this from the dividend (30).
2 12 | 30 -24 6 -
Interpret the remainder: The result of the subtraction (6) is the remainder. This means that 12 goes into 30 two times with a remainder of 6.
Therefore, 30 ÷ 12 = 2 with a remainder of 6. This can also be expressed as a mixed number: 2 6/12, which simplifies to 2 1/2. As a decimal, it's 2.5.
Alternative Calculation Methods
While long division is the standard method, other approaches can help solidify understanding:
-
Repeated Subtraction: Continuously subtract the divisor (12) from the dividend (30) until you reach a number less than the divisor. Count how many times you subtracted. This mirrors the "measurement" interpretation of division.
30 - 12 = 18 18 - 12 = 6
You subtracted twice, leaving a remainder of 6.
-
Fractions: Express the division as a fraction: 30/12. Simplify the fraction by finding the greatest common divisor (GCD) of 30 and 12, which is 6. Divide both the numerator and denominator by 6: (30 ÷ 6) / (12 ÷ 6) = 5/2. This fraction can be converted to a mixed number (2 1/2) or a decimal (2.5).
-
Using a Calculator: A calculator provides the quickest solution, but it's crucial to understand the underlying process.
The Significance of the Remainder
The remainder (6 in this case) is a critical part of the answer. It indicates that the division is not exact; 30 cannot be perfectly divided into 12 equal groups. The remainder represents the amount left over after the equal distribution.
The interpretation and significance of the remainder depend on the context of the problem. For instance:
-
Dividing cookies: If you have 30 cookies and want to divide them equally among 12 children, each child gets 2 cookies, and you have 6 cookies left over.
-
Measuring fabric: If you need 30 inches of fabric and your fabric comes in 12-inch lengths, you need to buy 3 lengths (2 lengths give you 24 inches, so you need one more to complete the 30 inches). The remainder is significant here, impacting purchasing decisions.
Visual Representation
Visualizing the problem can enhance understanding. Consider:
-
Circles or objects: Draw 30 circles and group them into sets of 12. You'll have two complete sets and 6 circles remaining.
-
Bar model: Draw a bar representing 30 units. Divide it into sections of 12 units each. You'll see two full sections and a remaining section of 6 units.
These visual aids can make abstract mathematical concepts more concrete and accessible.
Practical Applications of Division
Division is fundamental to numerous real-world situations:
-
Sharing equally: Distributing items (candy, money, tasks) among people fairly.
-
Calculating rates: Determining speed (distance divided by time), unit price (total cost divided by quantity), or fuel efficiency (miles driven divided by gallons used).
-
Scaling recipes: Adjusting ingredient quantities for a larger or smaller batch.
-
Averaging values: Finding the average score, temperature, or other data points.
-
Geometry: Calculating areas and volumes involving fractions.
Frequently Asked Questions (FAQs)
Q: Can I express the answer as a decimal instead of a mixed number?
A: Yes, 30 ÷ 12 = 2.5. Decimals are often preferred in scientific and engineering calculations.
Q: What if the remainder was zero?
A: A remainder of zero signifies that the division is exact; the divisor perfectly divides the dividend.
Q: How do I handle larger numbers in division problems?
A: The principles of long division remain the same, but the calculation might involve more steps. Using a calculator can be helpful for larger numbers.
Q: Is there a way to estimate the answer before calculating it precisely?
A: Yes, rounding can help estimate. Rounding 12 to 10, 30 ÷ 10 = 3, which provides a rough approximation. This helps with checking the reasonableness of your calculated answer.
Q: Why is understanding remainders important?
A: Remainders provide crucial information about the completeness of the division. Ignoring the remainder can lead to inaccuracies or impractical solutions in real-world applications. It signifies the "left-overs" and is critical for decision-making.
Conclusion
The seemingly straightforward calculation of 30 divided by 12 offers a rich opportunity to explore the fundamentals of division, different calculation methods, and the significance of the remainder. Understanding these concepts isn't just about solving math problems; it's about developing critical thinking skills applicable to a vast array of real-world scenarios. From sharing resources fairly to calculating rates and scaling quantities, division is a foundational mathematical tool with far-reaching implications. By grasping the different interpretations and approaches to division, you can confidently tackle more complex mathematical challenges and solve problems in diverse contexts. Remember to always consider the context of the problem when interpreting the final answer, including the remainder. This ensures that you apply your mathematical skills effectively and accurately in practical situations.
Latest Posts
Latest Posts
-
X 1 2 Expand
Sep 22, 2025
-
82 In To Ft
Sep 22, 2025
-
1 5 Gallon In Liters
Sep 22, 2025
-
68 8 Kg To Lbs
Sep 22, 2025
-
Swollen Lymph Nodes Preauricular
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 30 Divided By 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.