30 Out Of 42
renascent
Sep 18, 2025 · 5 min read
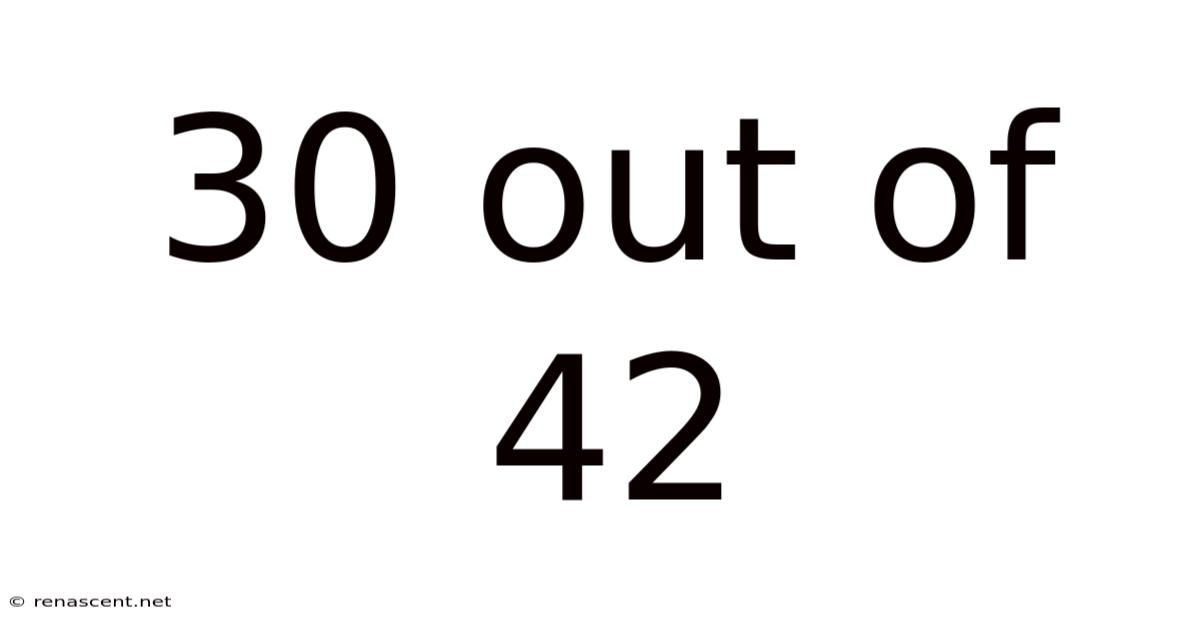
Table of Contents
Decoding 30 out of 42: Understanding Ratios, Percentages, and Their Real-World Applications
The seemingly simple phrase "30 out of 42" represents a fundamental concept in mathematics and statistics with far-reaching applications in everyday life. Understanding how to interpret and utilize this ratio, converting it to percentages, and grasping its implications is crucial for various fields, from academic assessments to financial analysis. This article delves deep into the meaning of "30 out of 42," exploring its mathematical representation, practical interpretations, and real-world examples. We'll also address common misconceptions and FAQs to ensure a complete understanding of this seemingly simple, yet powerful concept.
Understanding the Ratio: 30 out of 42
At its core, "30 out of 42" is a ratio. A ratio is a comparison of two numbers, showing the relative size of one quantity to another. In this case, it indicates that 30 represents a portion of a larger whole, 42. This could represent anything from the number of correct answers on a test to the number of successful sales calls made. The ratio can be expressed in several ways:
- Fraction: 30/42
- Colon notation: 30:42
- Verbal expression: 30 out of 42
Simplifying the Ratio: Finding the Lowest Common Denominator
Before proceeding, it's beneficial to simplify the ratio to its simplest form. This makes the ratio easier to understand and work with. To simplify 30/42, we need to find the greatest common divisor (GCD) of both numbers. The GCD of 30 and 42 is 6. Dividing both the numerator (30) and the denominator (42) by 6, we get:
30 ÷ 6 = 5 42 ÷ 6 = 7
Therefore, the simplified ratio is 5/7. This means that for every 7 items, 5 represent the specific portion being considered. This simplified form maintains the same proportional relationship as the original ratio, 30/42.
Converting to Percentage: A More Intuitive Representation
While the ratio 5/7 is accurate, percentages are often more intuitive and easily comparable. To convert a fraction to a percentage, we multiply the fraction by 100%.
(5/7) * 100% ≈ 71.43%
Therefore, "30 out of 42" represents approximately 71.43%. This percentage indicates that the portion represented by 30 is roughly 71.43% of the total 42.
Real-World Applications: From Test Scores to Financial Performance
The application of ratios and percentages like "30 out of 42" is widespread across numerous fields:
-
Academic Performance: Imagine a student scoring 30 out of 42 on a test. This translates to approximately 71.43%, a reasonably good score depending on the grading scale. The simplified ratio (5/7) shows a consistent performance pattern.
-
Sales and Marketing: A salesperson making 30 successful sales calls out of 42 attempts achieves a 71.43% success rate. This metric helps assess sales effectiveness and identify areas for improvement.
-
Quality Control: In manufacturing, 30 out of 42 products passing inspection indicates a 71.43% pass rate. This informs decisions on production processes and quality control measures.
-
Financial Analysis: Analyzing financial statements might involve comparing a company's current assets (30) to its total assets (42). The resulting percentage reveals the proportion of current assets relative to the total asset base.
-
Sports Statistics: A basketball player making 30 out of 42 free throws achieves a 71.43% free-throw percentage. This statistic reflects their shooting accuracy.
-
Survey Results: In a survey of 42 respondents, 30 answered "yes" to a particular question; this translates to a 71.43% positive response rate.
These examples demonstrate that the concept of "30 out of 42" or its simplified and percentage equivalents is remarkably versatile and essential for various data interpretations.
Beyond the Numbers: Understanding Context and Implications
It's critical to understand that the numerical value alone – 71.43% – doesn’t tell the whole story. The context is vital. For example:
-
A 71.43% score on a difficult exam is different from a 71.43% score on an easy exam. The difficulty of the test significantly impacts the meaning of the score.
-
A 71.43% success rate in sales might be excellent in one industry but poor in another. Industry benchmarks and expectations are crucial for proper interpretation.
-
A 71.43% pass rate in quality control might be acceptable for some products but unacceptable for others. The consequences of defects dictate the acceptable percentage.
Common Misconceptions and FAQs
Let's address some common misunderstandings:
Q: Is it always necessary to simplify the ratio?
A: While not strictly mandatory, simplifying a ratio makes it easier to understand and compare. It's particularly helpful when dealing with larger numbers.
Q: What if I have a different ratio, like 15 out of 21?
A: The same principles apply. 15/21 simplifies to 5/7, which is still approximately 71.43%. The underlying proportion remains consistent.
Q: Can I express this ratio as a decimal?
A: Absolutely! 5/7 ≈ 0.7143. Decimals, percentages, and fractions all represent the same proportional relationship.
Q: What about rounding?
A: Rounding is acceptable for clarity, but be mindful of potential errors in precision, especially in scientific or financial contexts. When possible, retain as many significant figures as necessary for accuracy.
Q: How can I improve my understanding of ratios and percentages?
A: Practice is key. Work through different examples, convert between fractions, decimals, and percentages, and try applying these concepts to real-world scenarios. Online resources and educational materials can be invaluable in enhancing your understanding.
Conclusion: Mastering Ratios and Percentages for a Broader Understanding
Understanding the concept of "30 out of 42," its simplified form (5/7), and its percentage equivalent (approximately 71.43%) is a fundamental skill with broad applications. This article has explored the mathematical underpinnings, practical interpretations, and real-world examples to illustrate its versatility. Remember that context is crucial; the numerical value alone is insufficient to fully understand the meaning and implications. By mastering ratios and percentages, you equip yourself with valuable tools for analyzing data, making informed decisions, and effectively communicating quantitative information across various fields. Continuous practice and a focus on contextual understanding will solidify this essential mathematical skill.
Latest Posts
Latest Posts
-
Three Subject Verb Disagreements
Sep 18, 2025
-
25 Mph To Km
Sep 18, 2025
-
Advantages For A Franchise
Sep 18, 2025
-
235 Kpa To Psi
Sep 18, 2025
-
26 2 Miles In Kilometres
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 30 Out Of 42 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.