30 Percent Of 70
renascent
Sep 16, 2025 · 5 min read
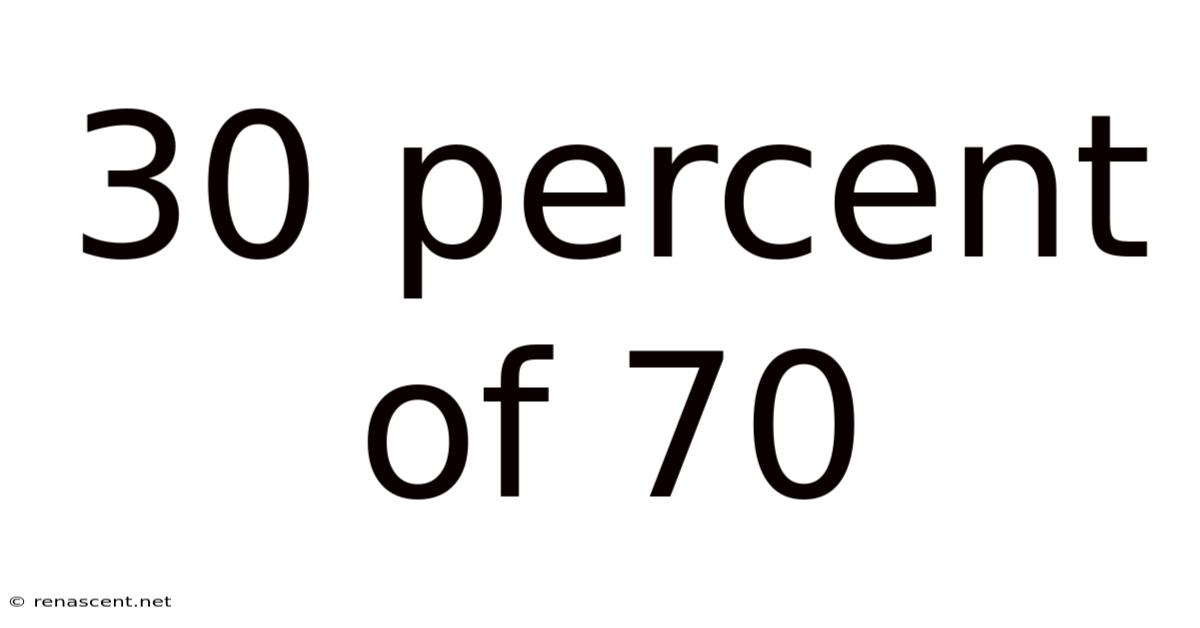
Table of Contents
Unveiling the Mystery: Calculating 30% of 70 and Mastering Percentage Calculations
Finding 30% of 70 might seem like a simple arithmetic problem, but understanding the underlying principles unlocks a world of practical applications in various fields, from everyday budgeting to complex financial analysis. This comprehensive guide will not only show you how to calculate 30% of 70 but also equip you with the knowledge and skills to tackle any percentage calculation with confidence. We'll explore different methods, delve into the mathematical concepts, and address frequently asked questions to ensure a thorough understanding.
Introduction: The Power of Percentages
Percentages are a fundamental aspect of mathematics used extensively in daily life. They represent a fraction of a whole, expressed as a number out of 100. Understanding percentages allows you to interpret data, make informed decisions, and solve problems across various disciplines, including finance, statistics, science, and even cooking. This article focuses on calculating 30% of 70, but the methods and principles discussed are applicable to a wide range of percentage problems. We’ll break down the process step-by-step, making it accessible to everyone, regardless of their mathematical background.
Method 1: The Fraction Method - A Simple Approach
The most straightforward way to calculate 30% of 70 is to convert the percentage into a fraction. Remember that a percentage is essentially a fraction with a denominator of 100. Therefore, 30% can be written as 30/100.
To find 30% of 70, we simply multiply 70 by the fraction 30/100:
70 * (30/100) = 2100/100 = 21
Therefore, 30% of 70 is 21.
Method 2: The Decimal Method – Efficiency and Precision
Another efficient method involves converting the percentage into a decimal. To do this, simply divide the percentage by 100. 30% divided by 100 is 0.30 or 0.3.
Now, multiply 70 by the decimal equivalent:
70 * 0.3 = 21
Again, we arrive at the answer: 30% of 70 is 21. This method is often preferred for its ease of use, especially when dealing with larger numbers or more complex calculations.
Method 3: Using Proportions – Understanding the Relationship
The concept of proportion provides a deeper understanding of percentage calculations. A proportion sets up an equivalence between two ratios. We can set up a proportion to solve for 30% of 70 as follows:
Let x represent 30% of 70
30/100 = x/70
To solve for x, we cross-multiply:
30 * 70 = 100 * x
2100 = 100x
x = 2100/100
x = 21
This method clearly demonstrates the relationship between the percentage, the whole (70), and the part we're trying to find (x). It's a valuable approach for developing a more intuitive grasp of percentage concepts.
Method 4: Mental Math Techniques – Speed and Accuracy
For simpler percentage calculations like this one, you can develop mental math techniques to quickly arrive at the answer. Notice that 30% is 3 times 10%. Finding 10% of a number is relatively easy – it's simply moving the decimal point one place to the left.
10% of 70 = 7
Since 30% is three times 10%, we multiply the result by 3:
7 * 3 = 21
This technique enhances calculation speed and reduces reliance on calculators, especially for common percentages like 10%, 20%, 25%, and 50%.
Expanding the Concept: Percentage Applications in Real-Life Scenarios
Understanding percentage calculations is crucial in numerous real-world situations:
-
Financial Calculations: Calculating discounts, interest rates, tax amounts, and profit margins all rely heavily on percentage calculations. For instance, if a store offers a 30% discount on a $70 item, you'd use this method to determine the discount amount.
-
Data Analysis: Percentages are essential for interpreting statistical data, representing proportions, and making comparisons. In market research, for instance, understanding the percentage of customers who prefer a certain product is critical for business decisions.
-
Scientific Calculations: Percentages are used to express concentrations, efficiency, and error margins in scientific experiments and data analysis.
-
Everyday Budgeting: Calculating percentages helps you track expenses, savings, and allocate resources effectively.
-
Cooking and Baking: Many recipes utilize percentages for precise ingredient measurements, particularly in baking where precise ratios are crucial for optimal results.
Scientific Explanation: The Mathematical Foundation of Percentages
Percentages are fundamentally based on the concept of fractions and proportions. A percentage represents a part of a whole, expressed as a fraction with a denominator of 100. The process of calculating a percentage involves converting the percentage into a fraction or decimal and then multiplying it by the whole value. This process is consistent across all percentage calculations, regardless of the specific numbers involved.
Frequently Asked Questions (FAQs)
- Q: How can I calculate other percentages of 70?
A: Use the methods outlined above, simply substituting the desired percentage for 30%. For example, to calculate 15% of 70, you would multiply 70 by 15/100 (or 0.15).
- Q: What if I need to calculate a percentage of a larger number?
A: The same methods apply, regardless of the size of the number. Simply substitute the appropriate values into the equations.
- Q: Are there online calculators for percentage calculations?
A: Yes, numerous online calculators are available that can quickly calculate percentages. However, understanding the underlying principles remains crucial for problem-solving and applying this knowledge in various situations.
- Q: How can I improve my skills in percentage calculations?
A: Practice regularly with various examples and problems. Start with simpler problems and gradually increase the complexity. Mastering the different methods – fraction, decimal, proportion – will provide a comprehensive understanding and increase your proficiency.
Conclusion: Mastering Percentages – A Stepping Stone to Mathematical Fluency
Calculating 30% of 70, while seemingly simple, provides a foundational understanding of percentage calculations. Mastering this skill opens doors to tackling more complex problems and applying this valuable knowledge across various academic and professional disciplines. By understanding the different methods and practicing regularly, you can develop confidence and proficiency in handling percentages, empowering you to make informed decisions and solve problems efficiently in your daily life. Remember that the key is to understand the underlying mathematical principles and adapt the methods to suit different scenarios. The more you practice, the more intuitive and efficient these calculations will become.
Latest Posts
Latest Posts
-
2 3 Of 17
Sep 16, 2025
-
91 6 Kg In Pounds
Sep 16, 2025
-
Big Rock Candy Lyrics
Sep 16, 2025
-
Fibrous Skeleton Of Heart
Sep 16, 2025
-
1 5 As A Decimal
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 30 Percent Of 70 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.