33/40 As A Percent
renascent
Sep 16, 2025 · 5 min read
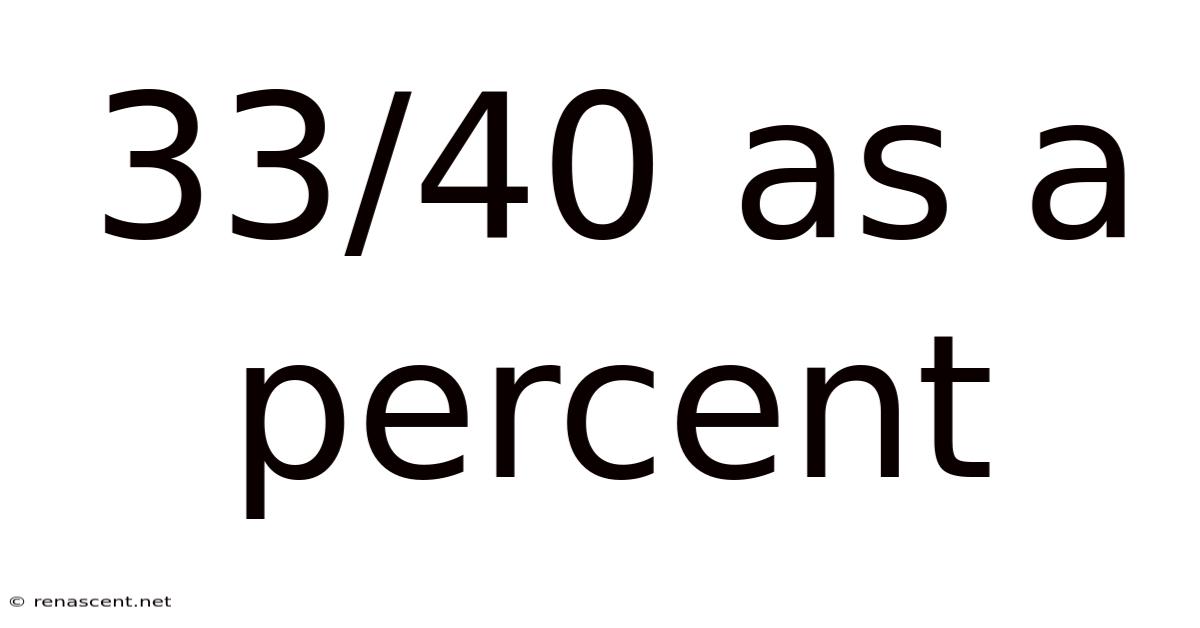
Table of Contents
33/40 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, crucial for various applications in everyday life and advanced studies. This comprehensive guide will delve into the process of converting the fraction 33/40 into a percentage, exploring the underlying principles, offering multiple approaches, and addressing common questions. We'll also explore the broader context of fraction-to-percentage conversions and their practical applications. By the end, you'll not only know the answer but also possess a solid understanding of the methodology.
Introduction: Understanding Fractions and Percentages
Before diving into the specific calculation of 33/40 as a percentage, let's establish a clear understanding of the concepts involved. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many parts make up the whole.
A percentage, denoted by the symbol %, represents a fraction out of 100. It expresses a proportion relative to a whole, which is considered as 100%. Percentages are widely used to express proportions in various contexts, from discounts and sales to statistical data and academic grades. The ability to convert between fractions and percentages allows for easier comparison and interpretation of different proportions.
Method 1: The Direct Conversion Method
The most straightforward way to convert a fraction to a percentage is to divide the numerator by the denominator and then multiply the result by 100. Let's apply this to 33/40:
-
Divide the numerator by the denominator: 33 ÷ 40 = 0.825
-
Multiply the result by 100: 0.825 × 100 = 82.5
Therefore, 33/40 is equal to 82.5%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
Another approach involves finding an equivalent fraction where the denominator is 100. This method is particularly helpful when the denominator is a factor of 100 or can be easily manipulated to become one. While not directly applicable to 33/40 in a simple way (40 is not a factor of 100), it demonstrates a valuable alternative technique for fractions with more convenient denominators.
Let's consider an example using a fraction where this method works more seamlessly, such as 25/50:
-
Determine the factor to multiply the denominator to reach 100: 50 needs to be multiplied by 2 to equal 100.
-
Multiply both the numerator and the denominator by the same factor: (25 × 2) / (50 × 2) = 50/100
-
Express as a percentage: 50/100 = 50%
Method 3: Using Proportions
The concept of proportions offers a powerful and flexible approach to solving this type of problem. A proportion states that two ratios are equal. We can set up a proportion to find the equivalent percentage:
-
Let x represent the percentage we are looking for.
-
Set up the proportion: 33/40 = x/100
-
Cross-multiply: 40x = 3300
-
Solve for x: x = 3300 ÷ 40 = 82.5
Therefore, 33/40 is equal to 82.5%. This method reinforces the underlying relationship between fractions and percentages.
Explanation of the Calculation and Underlying Principles
The core principle underlying the conversion of fractions to percentages is the concept of proportionality. A percentage is simply a fraction expressed with a denominator of 100. The calculations we performed essentially scale the original fraction to an equivalent fraction with a denominator of 100. This scaling is achieved by dividing the numerator by the denominator to find the decimal equivalent, and then multiplying by 100 to express this decimal as a percentage.
The decimal value obtained (0.825 in this case) represents the proportion of the whole that the fraction 33/40 constitutes. Multiplying by 100 converts this proportion into a percentage, indicating the relative size of the part compared to the whole (which is represented by 100%).
Practical Applications of Fraction-to-Percentage Conversions
The ability to convert fractions to percentages is widely applied in diverse fields:
-
Finance: Calculating interest rates, discounts, profit margins, and tax rates.
-
Statistics: Representing data proportions, probabilities, and survey results.
-
Science: Expressing experimental results, measurement errors, and concentration levels.
-
Education: Grading systems, assessing progress, and interpreting test scores.
-
Everyday Life: Calculating tips, understanding sales offers, and comparing values.
Frequently Asked Questions (FAQ)
Q: Can I convert any fraction to a percentage?
A: Yes, any fraction can be converted to a percentage using the methods described above. However, some fractions may result in percentages with recurring decimals, meaning the decimal part goes on infinitely without repeating.
Q: What if the percentage has a decimal? Does that mean it's incorrect?
A: No, a percentage can have a decimal. It simply indicates a more precise proportion than a whole number percentage. For instance, 82.5% is perfectly valid.
Q: Are there other ways to convert a fraction to a percentage?
A: While the methods mentioned are the most common and straightforward, there are alternative approaches involving the use of calculators or specialized software. However, understanding the underlying principles is crucial for mastering the conversion process.
Q: Why is understanding fraction-to-percentage conversion important?
A: This skill is essential for interpreting data, solving problems in various contexts, and making informed decisions in daily life and professional settings. It builds a foundation for more advanced mathematical concepts.
Q: What if I have a mixed number (e.g., 1 1/2)? How do I convert that to a percentage?
A: First, convert the mixed number into an improper fraction. For example, 1 1/2 becomes 3/2. Then, follow the steps outlined above for converting a fraction to a percentage.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting 33/40 to a percentage, which equals 82.5%, is a straightforward process that demonstrates fundamental mathematical principles. This guide has not only provided the answer but also equipped you with a deeper understanding of fractions, percentages, and the various methods for converting between them. By mastering this skill, you'll enhance your problem-solving abilities and gain valuable insights in various aspects of life and academic pursuits. The methods illustrated – direct conversion, equivalent fractions, and proportions – offer different approaches to arrive at the same correct answer, enabling flexibility and a more thorough grasp of the concepts involved. Remember that practice is key, and working through various examples will further solidify your understanding.
Latest Posts
Latest Posts
-
238 Pounds To Kg
Sep 16, 2025
-
Tomato And Beef Stew
Sep 16, 2025
-
136 Lbs To Kg
Sep 16, 2025
-
39 Divided By 2
Sep 16, 2025
-
Law And Order Noise
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 33/40 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.