35 8 Mixed Number
renascent
Sep 20, 2025 · 6 min read
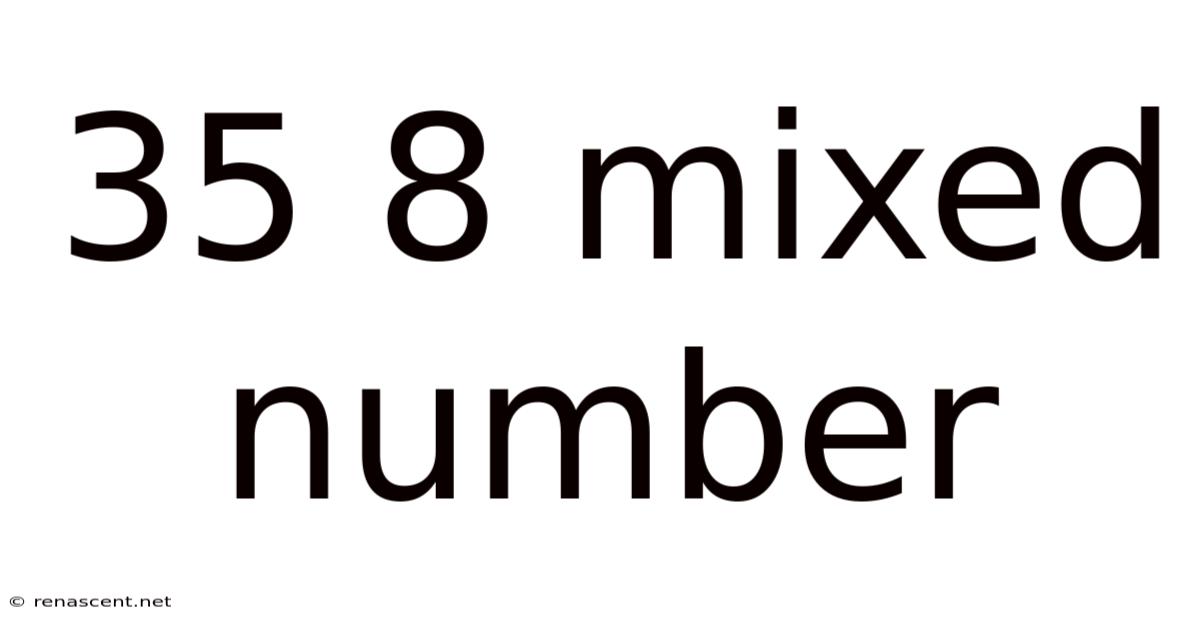
Table of Contents
Decoding the Mystery of 35 8: Understanding Mixed Numbers and Their Applications
Understanding mixed numbers is crucial for anyone navigating the world of mathematics, from elementary school students to advanced engineers. This comprehensive guide delves into the intricacies of mixed numbers, specifically focusing on the mixed number 35 8, explaining its composition, how to convert it to other forms, and demonstrating its applications in various real-world scenarios. We’ll also explore related concepts and answer frequently asked questions. By the end, you'll be confident in your understanding and ability to manipulate mixed numbers.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. It represents a quantity greater than one. For example, 35 8 means 35 whole units and 8/8 of another unit. In essence, it's a concise way to represent an improper fraction (a fraction where the numerator is greater than or equal to the denominator). The number 35 8 is particularly interesting because it already presents the whole number component clearly, simplifying the process of conversion and interpretation.
Understanding the Components of 35 8
The mixed number 35 8 consists of two main parts:
- The Whole Number: This represents the complete units. In 35 8, the whole number is 35.
- The Fraction: This represents a portion of a whole unit. In 35 8, the fraction is 8/8. This is a special case, representing a complete additional unit (8/8 = 1).
Converting 35 8 to an Improper Fraction
While 35 8 is easily understood in its mixed number form, converting it to an improper fraction is a valuable skill. This conversion is essential for performing certain mathematical operations. Here's how:
- Multiply the whole number by the denominator: 35 x 8 = 280
- Add the numerator: 280 + 8 = 288
- Keep the same denominator: The denominator remains 8.
- The improper fraction is: 288/8
Therefore, 35 8 is equivalent to the improper fraction 288/8. Note that this improper fraction can be simplified further, as we will see in the next section.
Simplifying Improper Fractions: The Case of 288/8
The improper fraction 288/8 can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 288 and 8 is 8. Dividing both the numerator and the denominator by 8, we get:
288 ÷ 8 = 36 8 ÷ 8 = 1
Therefore, the simplified improper fraction is 36/1, which is equal to 36. This confirms that 35 8 is indeed equivalent to 36. This simplification highlights the importance of reducing fractions to their simplest form for clarity and efficiency in calculations.
Converting 35 8 to a Decimal
Converting a mixed number to a decimal involves first converting it to an improper fraction, then dividing the numerator by the denominator. As we've already established, 35 8 simplifies to 36. Therefore, the decimal equivalent of 35 8 is 36.0.
Real-World Applications of Mixed Numbers
Mixed numbers are ubiquitous in everyday life. Here are some examples:
- Measurement: Imagine measuring ingredients for a recipe. You might need 2 1/2 cups of flour or 1 3/4 cups of sugar. These are classic examples of mixed numbers in action. Similarly, in construction or engineering, measurements often involve mixed numbers for accuracy and precision.
- Time: When dealing with time, we frequently use mixed numbers. For example, expressing a duration of 1 hour and 30 minutes as 1 1/2 hours is a common practice.
- Finance: Calculating interest or portions of payments often involves fractions, which can be represented as mixed numbers to provide a clearer understanding of the overall value.
- Data Analysis: Representing data values that are not whole numbers may be easily represented by mixed numbers to provide a better visual comprehension of data.
Specifically considering 35 8 (or its simplified form, 36), the applications are almost limitless:
- Counting objects: You might have 36 apples, 36 books, or 36 students in a class.
- Calculating costs: If an item costs $36, you'll use this whole number frequently.
- Representing quantities: Any whole quantity can be represented as a mixed number by adding an 8/8 component (or any other fraction equal to 1).
Further Exploration: Working with Other Mixed Numbers
The principles discussed here apply to all mixed numbers. Let's explore a few examples:
- 12 3/4: To convert this to an improper fraction, we multiply 12 by 4 (48), add 3 (51), and keep the denominator 4, resulting in 51/4.
- 5 1/2: This converts to 11/2 as an improper fraction.
- 27 7/9: This becomes (27 * 9 + 7)/9 = 243 + 7/9 = 250/9 as an improper fraction.
Remember to always simplify the improper fraction to its lowest terms whenever possible. This makes calculations easier and improves clarity.
Frequently Asked Questions (FAQ)
-
Q: Why are mixed numbers used?
- A: Mixed numbers provide a more intuitive and easily understood representation of quantities greater than one, combining whole units with fractional parts. They offer a balance between precision and readability, which is important in various contexts.
-
Q: Can I always convert a mixed number to a decimal?
- A: Yes, every mixed number can be converted to a decimal by first converting it to an improper fraction, then performing the division. However, some decimals may be non-terminating (repeating) if the fraction’s denominator contains prime factors other than 2 or 5.
-
Q: Is there a difference between an improper fraction and a mixed number?
- A: Yes, an improper fraction has a numerator greater than or equal to its denominator (e.g., 7/4), while a mixed number expresses the same quantity as a combination of a whole number and a proper fraction (e.g., 1 3/4). They represent the same value, just in different forms.
-
Q: How do I add or subtract mixed numbers?
- A: You can either convert the mixed numbers to improper fractions first, then add or subtract, or you can add/subtract the whole numbers separately and the fractions separately, then simplify the result.
-
Q: How do I multiply or divide mixed numbers?
- A: It's generally easiest to convert mixed numbers to improper fractions before performing multiplication or division. Then, perform the operation as you would with regular fractions.
Conclusion
The seemingly simple mixed number 35 8, when fully understood, unlocks a deeper appreciation for the versatile nature of mixed numbers. Through conversion to improper fractions and decimals, we see that the concept is fundamental across numerous mathematical applications and real-world scenarios. Mastering the manipulation of mixed numbers is a valuable skill that enhances problem-solving abilities and enhances clarity in various numerical representations. Remember to practice converting between different forms and applying these concepts to real-world situations to fully grasp their importance. The more you engage with mixed numbers, the more intuitive they become, building your confidence and competency in mathematics.
Latest Posts
Latest Posts
-
Molar Mass Of Alum
Sep 20, 2025
-
28 Oz To Kg
Sep 20, 2025
-
1 M To Kg
Sep 20, 2025
-
475 Divided By 3
Sep 20, 2025
-
81 Fahrenheit In Celsius
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 35 8 Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.