35 Divided By 2
renascent
Sep 21, 2025 · 6 min read
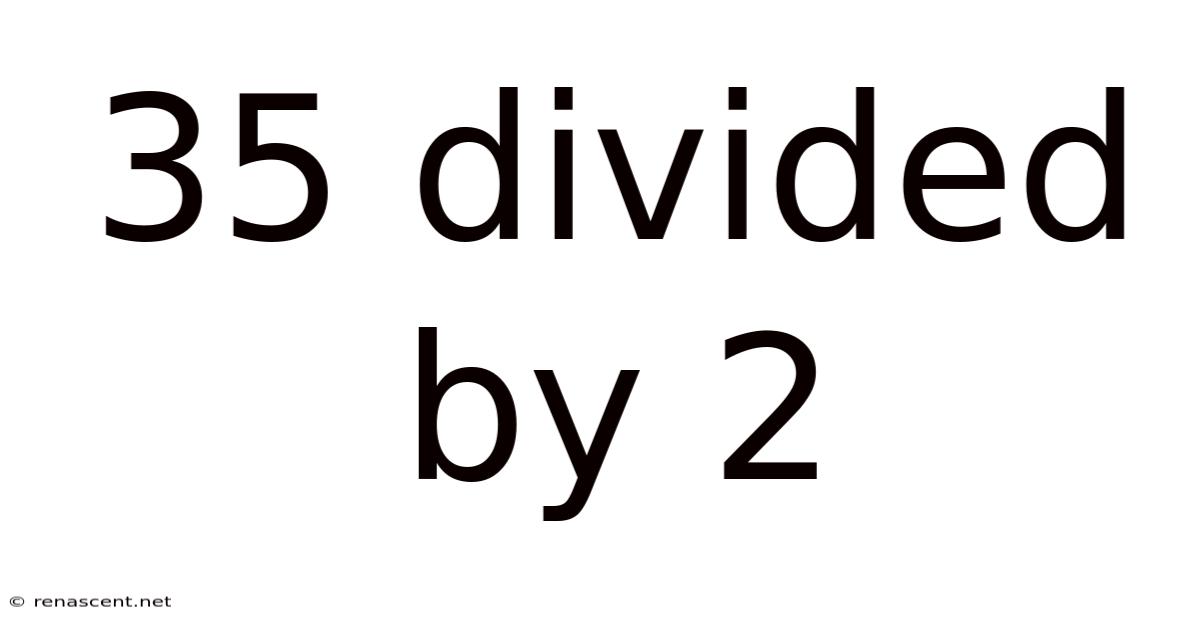
Table of Contents
Diving Deep into 35 Divided by 2: A Comprehensive Exploration of Division
This article delves into the seemingly simple calculation of 35 divided by 2, exploring not just the answer but the underlying mathematical concepts, different methods of solving the problem, and its practical applications. Understanding this seemingly basic division problem unlocks a deeper understanding of fractions, decimals, and the broader world of mathematics. 35 divided by 2 is a great starting point for exploring these fundamental concepts.
Introduction: Understanding Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts. In the case of 35 divided by 2, we're asking: "How many times does 2 fit into 35?" or equivalently, "What is the result of sharing 35 items equally among 2 people?"
The standard notation for division is 35 ÷ 2, 35/2, or $\frac{35}{2}$. All three notations represent the same mathematical operation.
Method 1: Long Division
The traditional method of solving this problem is through long division. This method provides a step-by-step approach that helps visualize the process.
-
Set up the problem: Write 35 as the dividend (the number being divided) and 2 as the divisor (the number dividing the dividend).
2 | 35 -
Divide the tens digit: How many times does 2 go into 3 (the tens digit of 35)? It goes in once (2 x 1 = 2). Write the 1 above the 3.
1 2 | 35 -
Subtract: Subtract the result (2) from the tens digit (3): 3 - 2 = 1.
1 2 | 35 -2 1 -
Bring down the units digit: Bring down the units digit (5) next to the remainder (1), forming the number 15.
1 2 | 35 -2 15 -
Divide the new number: How many times does 2 go into 15? It goes in 7 times (2 x 7 = 14). Write the 7 above the 5.
17 2 | 35 -2 15 -
Subtract again: Subtract the result (14) from 15: 15 - 14 = 1.
17 2 | 35 -2 15 -14 1 -
Interpret the result: The quotient (the result of the division) is 17, and the remainder is 1. This means that 35 divided by 2 is 17 with a remainder of 1. We can express this as 17 R1.
Method 2: Fractions
Another way to represent the answer is using fractions. Since we have a remainder, the result isn't a whole number. The remainder becomes the numerator of a fraction, and the divisor becomes the denominator. Therefore, 35 divided by 2 can be expressed as:
$\frac{35}{2} = 17\frac{1}{2}$
This means 17 and a half. This fractional representation is often more useful in practical scenarios where dealing with whole numbers alone isn't sufficient.
Method 3: Decimals
We can also express the result as a decimal. To do this, we continue the long division process beyond the whole number part. After obtaining the remainder of 1, we add a decimal point to the dividend (35) and add a zero.
17.5
2 | 35.0
-2
15
-14
10
-10
0
Now, 2 goes into 10 five times. Therefore, 35 divided by 2 is 17.5. This decimal representation is highly useful in many practical applications requiring precision.
Understanding the Remainder
The remainder (1 in this case) represents the part of the dividend that couldn't be equally divided by the divisor. In the context of sharing 35 items between two people, one person would get 17 items, and the other would get 17 items, leaving one item remaining. This remainder can be handled in different ways depending on the context:
- It can be discarded: If the remainder is insignificant to the problem.
- It can be shared: The remainder can be divided further (in this case, each person gets an extra 0.5 items).
- It can form a fraction or decimal: As shown in the previous sections.
Practical Applications
The division of 35 by 2, while seemingly simple, has various practical applications:
- Sharing resources: Dividing items, money, or tasks equally among two people.
- Calculating averages: Finding the average of two numbers. For example, if someone scored 30 and 40 on two tests, the average is (30 + 40) / 2 = 35. If you then needed to divide that average by 2, you'd use this calculation.
- Scaling recipes: Halving a recipe that calls for 35 units of an ingredient.
- Measuring and cutting: Dividing a length of 35 units into two equal parts.
- Geometry and area: Calculations related to areas and dimensions often involve division.
Beyond the Basics: Exploring Further Mathematical Concepts
This seemingly simple problem can serve as a springboard for exploring more advanced mathematical concepts:
- Modular Arithmetic: The remainder (1) is crucial in modular arithmetic, a system where numbers "wrap around" after reaching a certain value (the modulus). This is used extensively in cryptography and computer science.
- Number Theory: The concepts of divisors, remainders, and prime factorization are fundamental in number theory, a branch of mathematics focused on the properties of integers.
- Algebra: The equation 2x = 35 can be solved using division to find the value of x (x = 35/2 = 17.5).
- Calculus: The concept of limits and derivatives are built upon foundational arithmetic operations like division.
Frequently Asked Questions (FAQ)
-
Q: What is the most accurate answer to 35 divided by 2?
A: The most accurate answer depends on the context. 17 R1, 17 ½, and 17.5 are all correct representations, each suitable for different scenarios.
-
Q: Can you divide 35 by 2 without using long division?
A: Yes, you can use fractions or a calculator. You can also mentally estimate that 2 goes into 30 fifteen times, and then add the remaining 5, which divided by 2 is 2.5. This totals 17.5.
-
Q: What if I get a different answer?
A: Double-check your calculations. Ensure you've followed the steps of long division accurately or used a calculator correctly.
-
Q: Why is understanding division important?
A: Division is a fundamental operation used in countless everyday situations and is the foundation for many advanced mathematical concepts.
Conclusion: Mastering the Fundamentals
The seemingly simple calculation of 35 divided by 2 offers a rich opportunity to explore fundamental mathematical concepts. Understanding different methods of solving this problem, interpreting the remainder, and recognizing its practical applications are vital for building a strong foundation in mathematics. This exploration goes beyond simply getting the answer; it's about understanding why the answer is what it is and how this simple operation connects to a much wider mathematical landscape. From fractions and decimals to modular arithmetic and beyond, this seemingly simple problem unlocks a world of mathematical understanding. Mastering such fundamentals is key to success in more advanced mathematical studies and numerous real-world applications.
Latest Posts
Latest Posts
-
166 Min To Hours
Sep 21, 2025
-
Rudy In Ice Age
Sep 21, 2025
-
150 Gm To Oz
Sep 21, 2025
-
1 7 Kgs In Pounds
Sep 21, 2025
-
Ammo Can 50 Cal
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 35 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.