36 Out Of 80
renascent
Sep 17, 2025 · 6 min read
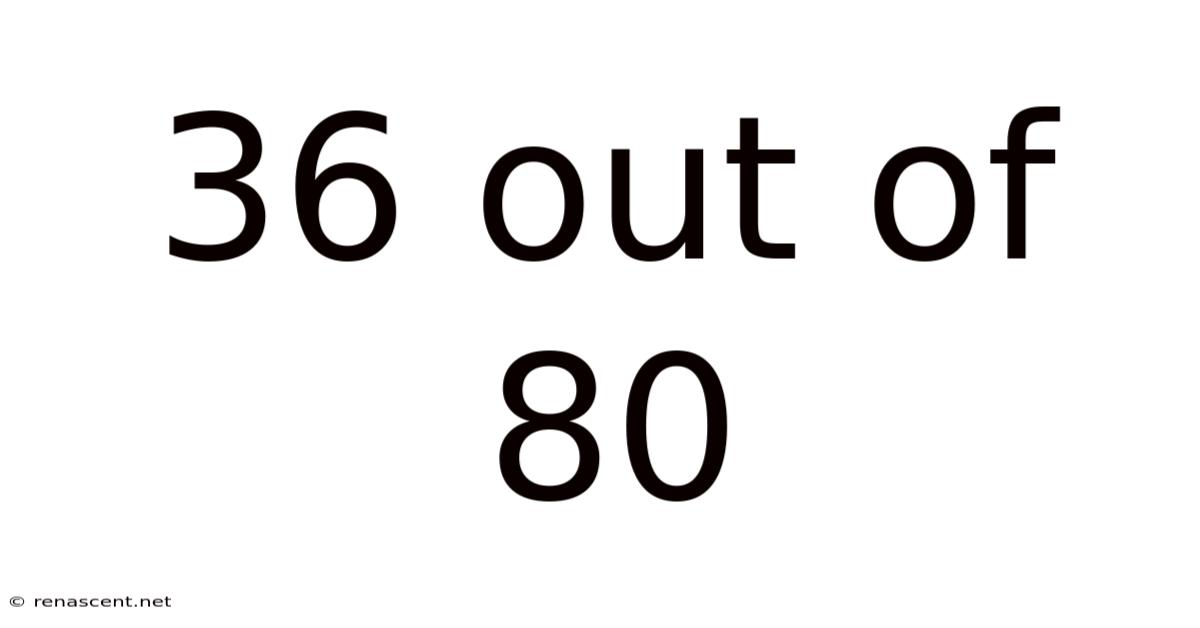
Table of Contents
Decoding 36 out of 80: Understanding Fractions, Percentages, and Their Applications
The seemingly simple fraction 36 out of 80 represents a concept that extends far beyond basic arithmetic. Understanding how to express this ratio, simplify it, convert it to a percentage, and ultimately apply it in various contexts is a fundamental skill with broad applications in everyday life, academic pursuits, and professional settings. This article will provide a comprehensive guide to interpreting and working with 36 out of 80, exploring its mathematical representation, practical applications, and common misunderstandings.
Understanding the Basics: Fractions and Ratios
Before delving into the specifics of 36 out of 80, let's establish a clear understanding of fractions and ratios. A fraction represents a part of a whole. It's expressed as a numerator (the top number) over a denominator (the bottom number), indicating how many parts are being considered out of the total number of parts. In our case, 36 out of 80 can be written as the fraction 36/80.
A ratio, on the other hand, compares two quantities. While similar to a fraction, it doesn't necessarily imply a part of a whole. The ratio of 36 to 80 indicates the relative size of these two numbers. Both fractions and ratios can be simplified to their lowest terms.
Simplifying the Fraction 36/80
Simplifying a fraction means reducing it to its simplest form while retaining its value. This is achieved by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. Let's find the GCD of 36 and 80.
The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36. The factors of 80 are 1, 2, 4, 5, 8, 10, 16, 20, 40, and 80.
The greatest common factor of 36 and 80 is 4. Dividing both the numerator and the denominator by 4, we get:
36 ÷ 4 = 9 80 ÷ 4 = 20
Therefore, the simplified fraction is 9/20. This simplified fraction represents the same value as 36/80 but is easier to work with.
Converting the Fraction to a Percentage
Percentages are a way of expressing a fraction or ratio as a portion of 100. To convert the fraction 9/20 to a percentage, we need to find an equivalent fraction with a denominator of 100. We can do this by multiplying both the numerator and the denominator by 5:
(9 × 5) / (20 × 5) = 45/100
45/100 is equivalent to 45%. This means that 36 out of 80 represents 45% of the total.
Real-World Applications of 36/80 (or 45%)
The ability to interpret and work with fractions and percentages like 36/80 (45%) is crucial in many real-world scenarios:
-
Academic Performance: Imagine a student scoring 36 out of 80 on a test. Understanding that this equates to 45% allows for a clear assessment of their performance. This percentage can be compared to other scores, class averages, or grading scales to determine the student's standing.
-
Business and Finance: In business, 45% could represent various metrics, such as market share, sales conversion rates, or project completion progress. This percentage provides a concise and easily understandable measure of performance. For instance, a company might aim to increase its 45% market share to a higher percentage.
-
Data Analysis: In data analysis, percentages are used to summarize and interpret data sets. For example, if a survey of 80 people reveals that 36 prefer a particular product, then 45% is a key statistic reflecting consumer preference.
-
Everyday Life: We encounter percentages daily, from sales discounts (e.g., a 45% off sale) to interest rates on loans and savings accounts. Understanding these percentages is essential for making informed financial decisions.
-
Sports Statistics: In sports, percentages are widely used to represent batting averages, free-throw percentages, or winning percentages. For example, a basketball player with a 45% free-throw percentage would make 45 out of every 100 free throws on average.
Understanding the Decimal Equivalent
Besides fractions and percentages, the value 36/80 can also be expressed as a decimal. To convert a fraction to a decimal, divide the numerator by the denominator:
36 ÷ 80 = 0.45
Therefore, 36 out of 80 is equivalent to 0.45 as a decimal. This decimal representation is often used in calculations and data analysis.
Common Misconceptions and Pitfalls
Several common misunderstandings can arise when working with fractions, percentages, and ratios:
-
Incorrect Simplification: Failing to find the greatest common divisor can lead to an incorrectly simplified fraction. Always ensure you've found the largest common factor to obtain the simplest form.
-
Misinterpreting Percentages: Confusing percentages with absolute values is a common error. 45% of a large number is significantly different from 45% of a small number.
-
Ignoring Context: The meaning of 45% depends heavily on the context. A 45% score on a test might be considered failing, while a 45% market share could be a considerable success.
-
Rounding Errors: When converting between fractions, decimals, and percentages, rounding errors can accumulate. It's important to retain as much precision as possible during calculations to minimize errors.
Frequently Asked Questions (FAQ)
-
Q: How do I calculate 45% of a different number? A: To calculate 45% of any number, multiply the number by 0.45 (the decimal equivalent of 45%). For example, 45% of 100 is 100 × 0.45 = 45.
-
Q: What is the ratio of the remaining portion to the total? A: If 36 out of 80 represents 45%, then the remaining portion is 80 - 36 = 44. The ratio of the remaining portion to the total is 44/80, which simplifies to 11/20 or 55%.
-
Q: Can I express this as a proportion? A: Yes, the proportion can be written as 36:80 or 9:20. This shows the relationship between the two numbers.
-
Q: What if the numbers are not whole numbers? A: The principles remain the same. You would still simplify the fraction, convert to a percentage, or find the decimal equivalent. The process might involve more complex calculations depending on the numbers involved.
Conclusion
Understanding the relationship between fractions, percentages, and decimals is a crucial skill for navigating various aspects of life. The seemingly simple concept of 36 out of 80 provides a practical starting point for grasping these fundamental mathematical concepts. By mastering the techniques of simplification, conversion, and application, we can effectively analyze data, make informed decisions, and confidently interpret numerical information encountered in diverse contexts. The ability to move fluently between fractional, percentage, and decimal representations of a ratio empowers individuals to tackle more complex mathematical challenges and excel in quantitative fields. Remember to always consider the context, avoid common pitfalls, and utilize the appropriate tools to solve problems accurately and efficiently.
Latest Posts
Latest Posts
-
4 7 As Percent
Sep 17, 2025
-
8 X 1 5
Sep 17, 2025
-
1 5 16 In Mm
Sep 17, 2025
-
24 Millimeters To Inches
Sep 17, 2025
-
107 Kg To Pounds
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 36 Out Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.