360 Divided By 3
renascent
Sep 22, 2025 · 6 min read
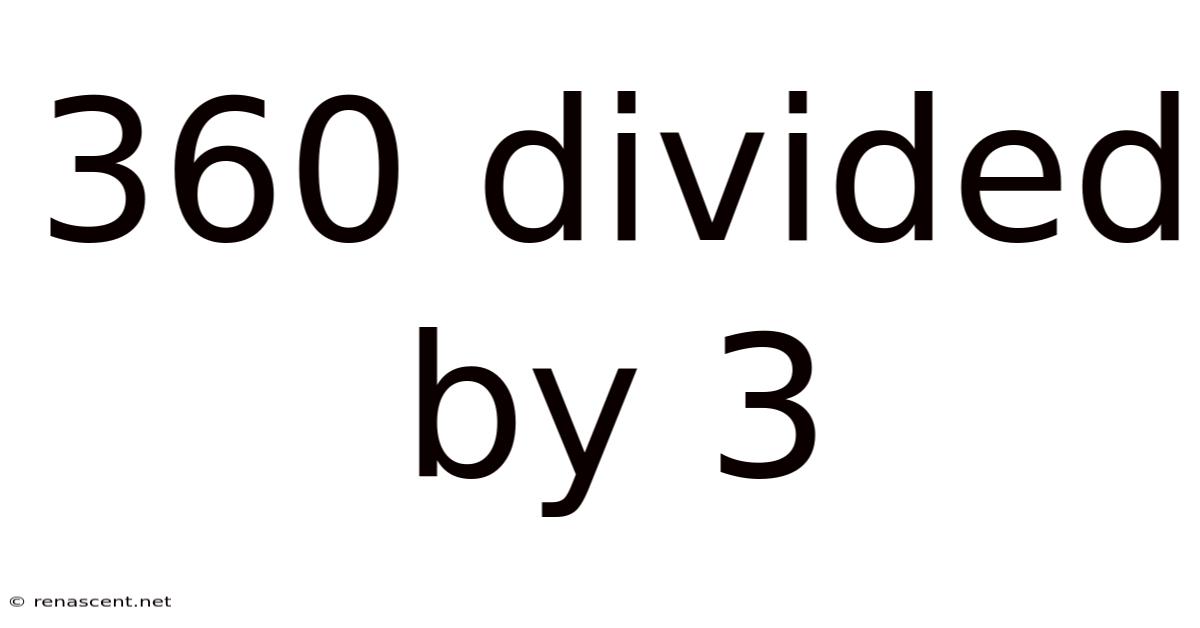
Table of Contents
Unveiling the Simplicity: A Deep Dive into 360 Divided by 3
Dividing 360 by 3 might seem like a simple arithmetic problem, something easily solved with a calculator or a quick mental calculation. However, this seemingly straightforward operation opens doors to a broader understanding of mathematical principles, from basic division to more complex concepts like factors, multiples, and even the geometry of circles. This article will delve into the solution, explore the underlying mathematical concepts, and examine the real-world applications of this seemingly simple division problem. We'll even address common misconceptions and frequently asked questions.
Understanding the Basics: Division and its Components
Before we tackle 360 divided by 3, let's refresh our understanding of division. Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a whole quantity into equal parts. In the expression "a ÷ b," 'a' is the dividend (the number being divided), 'b' is the divisor (the number dividing the dividend), and the result is the quotient. Any remaining amount after the equal division is called the remainder.
In our case, 360 is the dividend, and 3 is the divisor. We are seeking the quotient that represents the result of dividing 360 into 3 equal parts.
Solving 360 Divided by 3: Multiple Approaches
There are several ways to solve 360 ÷ 3:
1. Long Division:
This classic method is a step-by-step process that's excellent for understanding the mechanics of division.
- Step 1: Divide the hundreds digit (3) by the divisor (3). 3 ÷ 3 = 1. Write '1' above the 3 in the hundreds place.
- Step 2: Multiply the quotient (1) by the divisor (3). 1 x 3 = 3. Write '3' below the 3 in the hundreds place.
- Step 3: Subtract the result (3) from the hundreds digit (3). 3 - 3 = 0.
- Step 4: Bring down the tens digit (6).
- Step 5: Divide the tens digit (6) by the divisor (3). 6 ÷ 3 = 2. Write '2' above the 6 in the tens place.
- Step 6: Multiply the quotient (2) by the divisor (3). 2 x 3 = 6. Write '6' below the 6 in the tens place.
- Step 7: Subtract the result (6) from the tens digit (6). 6 - 6 = 0.
- Step 8: Bring down the units digit (0).
- Step 9: Divide the units digit (0) by the divisor (3). 0 ÷ 3 = 0. Write '0' above the 0 in the units place.
- Step 10: The final result (quotient) is 120.
2. Mental Math:
For those comfortable with mental calculations, this problem is easily solvable. Knowing that 3 x 100 = 300 and 3 x 20 = 60, you can quickly add these to get 360. Therefore, 360 ÷ 3 = 120.
3. Using a Calculator:
The simplest approach is to use a calculator. Inputting "360 ÷ 3" will instantly give you the answer: 120.
Beyond the Answer: Exploring Mathematical Concepts
The simple answer, 120, opens up a world of mathematical exploration. Let's delve into some related concepts:
1. Factors and Multiples:
The number 3 is a factor of 360 because it divides 360 evenly without leaving a remainder. Conversely, 360 is a multiple of 3. Understanding factors and multiples is crucial in various mathematical applications, including simplifying fractions and solving algebraic equations.
2. Divisibility Rules:
The divisibility rule for 3 states that a number is divisible by 3 if the sum of its digits is divisible by 3. Let's test this with 360: 3 + 6 + 0 = 9. Since 9 is divisible by 3, we confirm that 360 is divisible by 3. This rule is a quick way to check for divisibility without performing the actual division.
3. Prime Factorization:
Prime factorization breaks down a number into its prime factors (numbers divisible only by 1 and themselves). The prime factorization of 360 is 2³ x 3² x 5. This decomposition is fundamental in many areas of mathematics, particularly in number theory and algebra.
4. Geometry and Circles:
The number 360 is significantly linked to geometry, specifically circles. A circle contains 360 degrees. Dividing 360 by 3 could represent dividing a circle into three equal sectors, each with a central angle of 120 degrees. This has applications in various fields, such as architecture, engineering, and cartography.
Real-World Applications: Where Does This Matter?
The seemingly simple operation of 360 ÷ 3 has practical applications in diverse fields:
- Baking: Dividing a recipe that yields 360 cookies into three equal batches.
- Construction: Calculating the number of sections in a structure where each part is one-third of the total length of 360 units.
- Finance: Dividing a total investment amount among three different investment vehicles.
- Data Analysis: Distributing a dataset of 360 elements across three categories for analysis.
- Time Management: Dividing a 360-minute project into three equal phases of 120 minutes each.
Addressing Common Questions and Misconceptions
Let's address some frequently asked questions and common misconceptions related to division:
Q: What if I divide 360 by a number that doesn't divide evenly?
A: If the divisor doesn't divide the dividend evenly, you'll have a remainder. For instance, 360 ÷ 7 = 51 with a remainder of 3. The remainder signifies the portion that couldn't be divided equally.
Q: Is there a difference between dividing by 3 and multiplying by 1/3?
A: No, dividing by 3 is equivalent to multiplying by its reciprocal, 1/3. Both operations produce the same result: 120.
Q: Why is understanding division important?
A: Division is a fundamental arithmetic operation crucial for problem-solving in everyday life and advanced mathematical concepts. It's essential for understanding ratios, proportions, fractions, and many other mathematical principles.
Q: Can I use a different method to solve 360 ÷ 3?
A: Absolutely! You can use any method you find comfortable and efficient, be it long division, mental math, or a calculator. The most important aspect is understanding the underlying concept and achieving the correct result.
Conclusion: Embracing the Power of Simple Arithmetic
While the division problem 360 ÷ 3 might seem trivial at first glance, its solution, 120, unlocks a wealth of mathematical understanding and practical applications. From basic division principles to the complexities of factors, multiples, and geometry, this simple operation provides a stepping stone to a deeper appreciation of the elegance and utility of mathematics in various aspects of our lives. Remember, even the most straightforward mathematical concepts can hold hidden depths and profound implications when examined closely. So, the next time you encounter a seemingly simple calculation, take a moment to appreciate the underlying mathematical principles and its potential real-world applications.
Latest Posts
Latest Posts
-
61 Celsius To Fahrenheit
Sep 22, 2025
-
Temperature For A Bath
Sep 22, 2025
-
R And R Fencing
Sep 22, 2025
-
45 Minutes In Seconds
Sep 22, 2025
-
300 Kg To Lbs
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 360 Divided By 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.