39/40 As A Percentage
renascent
Sep 21, 2025 · 5 min read
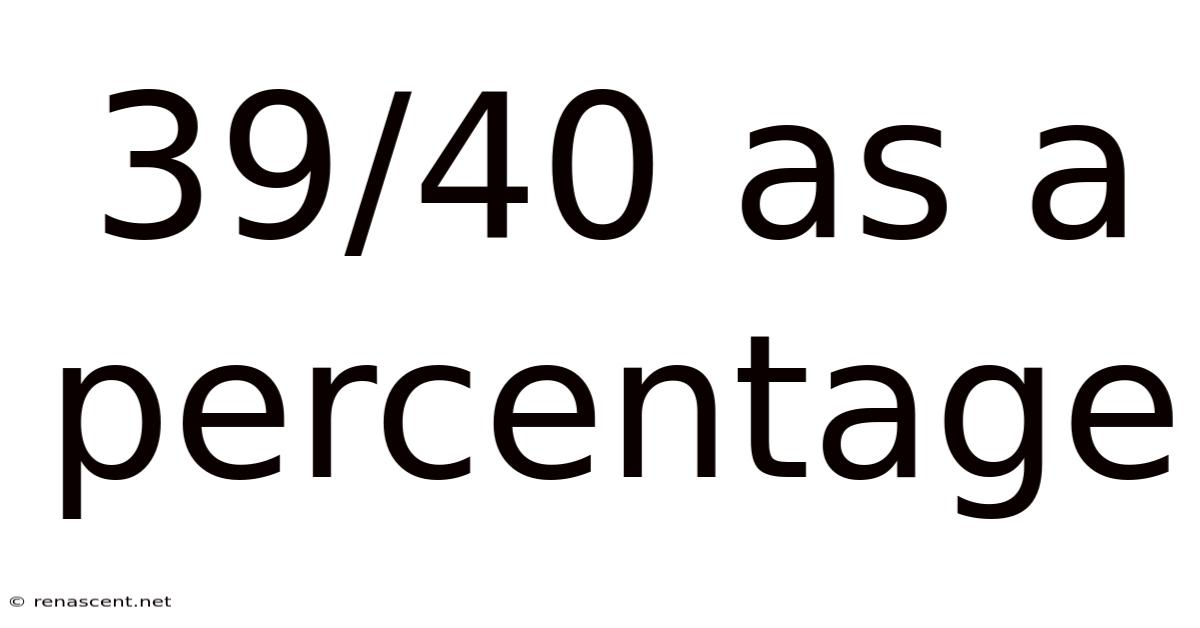
Table of Contents
39/40 as a Percentage: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, with applications spanning various fields from finance and statistics to everyday life. This article delves into the conversion of the fraction 39/40 into a percentage, providing a detailed explanation, practical examples, and addressing frequently asked questions. We'll explore the underlying mathematical principles and offer strategies to confidently tackle similar conversions. By the end, you'll not only know the answer but also understand the process thoroughly.
Introduction: Why Convert Fractions to Percentages?
Fractions and percentages are two different ways of expressing parts of a whole. While fractions represent parts as a ratio of two numbers (numerator/denominator), percentages express parts as a proportion of 100. Percentages are often preferred in many contexts because they provide a standardized and easily comparable way to represent proportions. For instance, understanding that a student scored 97.5% on a test is immediately more intuitive than knowing they scored 39/40. This ease of comprehension is why percentage conversions are so crucial.
Step-by-Step Conversion of 39/40 to Percentage
The process of converting a fraction to a percentage involves two key steps:
1. Convert the Fraction to a Decimal:
To convert a fraction to a decimal, we simply divide the numerator (the top number) by the denominator (the bottom number). In this case:
39 ÷ 40 = 0.975
2. Convert the Decimal to a Percentage:
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%).
0.975 x 100 = 97.5%
Therefore, 39/40 is equal to 97.5%.
Understanding the Math Behind the Conversion
The core principle underlying this conversion lies in the definition of a percentage. A percentage is simply a fraction with a denominator of 100. When we convert a fraction like 39/40 to a percentage, we are essentially finding an equivalent fraction with a denominator of 100. This can be represented mathematically as:
(39/40) * (100/100) = (3900/4000)
Simplifying this fraction by dividing both the numerator and the denominator by 40 gives us:
(3900/4000) = (97.5/100) = 97.5%
This demonstrates that multiplying the original fraction by 100/100 (which is equal to 1 and doesn't change the value) allows us to express the fraction as a percentage. The multiplication by 100 effectively scales the fraction to a base of 100, which is the essence of the percentage representation.
Practical Applications of Percentage Conversions
The ability to convert fractions to percentages is valuable in numerous real-world scenarios:
- Academic Performance: Calculating grades, test scores, and overall academic progress. A score of 39 out of 40 on a test directly translates to a 97.5% grade, providing a clear and easily understood representation of performance.
- Financial Calculations: Determining interest rates, discounts, profit margins, and tax rates. Understanding percentages is fundamental in managing personal finances and making informed financial decisions.
- Data Analysis and Statistics: Representing proportions and distributions in data sets. Percentages provide a standardized way to compare and interpret different data points.
- Everyday Life: Calculating tips, sales discounts, and understanding proportions in recipes or measurements. The ability to quickly convert fractions to percentages is beneficial in various everyday situations.
Alternative Methods for Converting Fractions to Percentages
While the method described above is the most straightforward, other approaches can be used, particularly for fractions that are easily converted to simpler forms:
-
Using Equivalent Fractions: If the denominator of the fraction is a factor of 100 (like 25, 50, or 100), you can directly convert it to a percentage by finding an equivalent fraction with a denominator of 100. For example, 1/4 can easily be converted to 25/100, which is 25%. However, this method is less efficient for fractions like 39/40.
-
Using Proportions: You can set up a proportion to solve for the percentage. For example:
39/40 = x/100
Solving for x (by cross-multiplying) gives you:
40x = 3900
x = 97.5
This method is mathematically equivalent to the initial method but can be helpful in visualizing the relationship between the fraction and the percentage.
Advanced Considerations and Extensions
The conversion of 39/40 to a percentage highlights the fundamental relationship between fractions, decimals, and percentages. This understanding can be extended to more complex scenarios involving:
- Percentages greater than 100%: If the numerator is larger than the denominator, the resulting percentage will be greater than 100%. This indicates a proportion exceeding the whole.
- Working with mixed numbers: A mixed number (a whole number and a fraction) needs to be converted to an improper fraction before applying the conversion steps outlined above.
- Dealing with recurring decimals: Some fractions, when converted to decimals, result in recurring decimals. In these cases, it's common practice to round the decimal to a specified number of decimal places before converting to a percentage.
Frequently Asked Questions (FAQs)
-
Q: What if I have a complex fraction?
A: A complex fraction is a fraction where the numerator or denominator (or both) is itself a fraction. To convert a complex fraction to a percentage, simplify the complex fraction into a single fraction first, then apply the standard conversion steps.
-
Q: How accurate should my percentage be?
A: The level of accuracy depends on the context. In many cases, rounding to one or two decimal places is sufficient. For highly precise calculations, more decimal places may be necessary.
-
Q: Can I use a calculator to convert fractions to percentages?
A: Yes, most calculators have the capability to perform this conversion directly. Simply divide the numerator by the denominator and then multiply the result by 100.
-
Q: What are some common mistakes to avoid?
A: A common mistake is forgetting to multiply the decimal by 100 when converting to a percentage. Another is incorrectly interpreting the fraction, particularly with complex fractions.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a valuable skill with wide-ranging applications. The conversion of 39/40 to 97.5% serves as a clear example of this process. Understanding the mathematical principles behind the conversion and mastering the steps involved will empower you to confidently handle similar calculations across various contexts. Remember to always double-check your work and consider the appropriate level of accuracy required for the specific situation. By understanding the fundamental concepts and practicing the methods, you'll become proficient in converting fractions to percentages and unlock a deeper understanding of proportional relationships.
Latest Posts
Latest Posts
-
White Belt Blox Fruits
Sep 21, 2025
-
Alice In Wonderland Food
Sep 21, 2025
-
Repeating Sequence Crossword Clue
Sep 21, 2025
-
60 4 Kg To Pounds
Sep 21, 2025
-
Best Home Photo Printer
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 39/40 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.