4 25 Square Root
renascent
Sep 17, 2025 · 5 min read
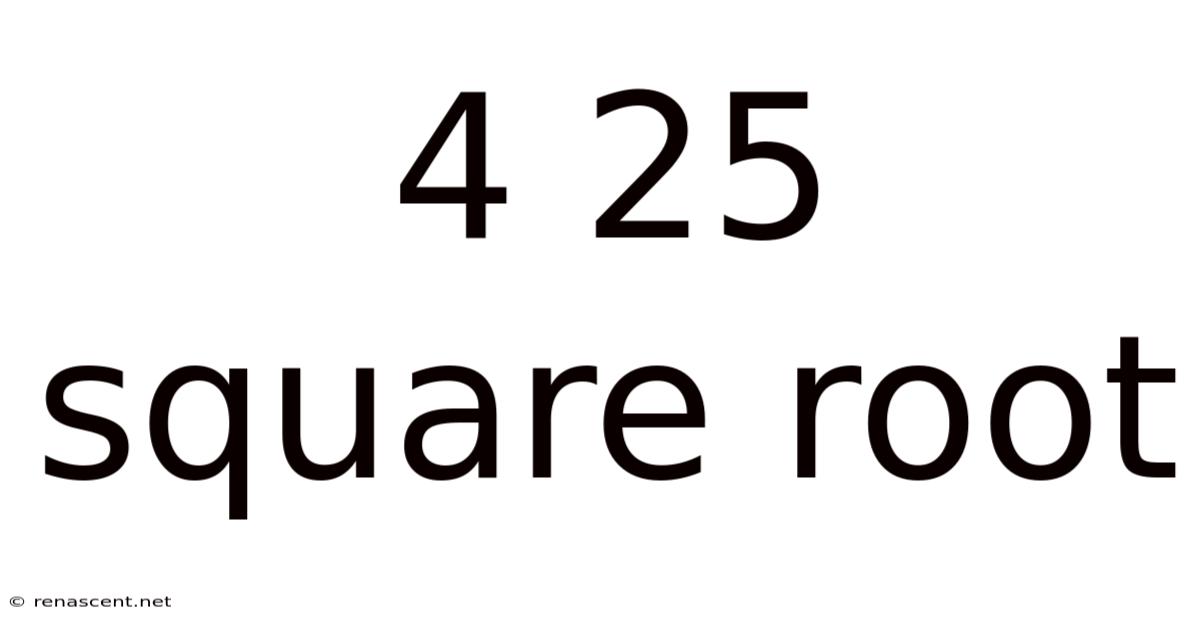
Table of Contents
Decoding the Mystery: Understanding the Square Root of 4.25
The square root of 4.25, often written as √4.25, might seem like a simple mathematical problem at first glance. However, delving into its calculation reveals a fascinating interplay of mathematical concepts and techniques. This comprehensive guide will explore various methods for calculating √4.25, explain the underlying principles, and address common questions surrounding this seemingly straightforward calculation. Understanding this seemingly simple square root opens doors to a deeper appreciation of numerical analysis and its applications in various fields.
Understanding Square Roots: A Quick Refresher
Before we dive into the specifics of √4.25, let's refresh our understanding of square roots. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. This concept is fundamental to many areas of mathematics, including algebra, geometry, and calculus. Square roots can be found for positive numbers, resulting in both positive and negative solutions (though typically, only the positive solution is considered).
Method 1: Using a Calculator
The most straightforward method for finding the square root of 4.25 is to use a calculator. Most scientific calculators and even basic ones have a square root function (√) usually represented by a button. Simply enter 4.25 and press the square root button. The calculator will quickly provide the answer, which is approximately 2.06155. This method offers speed and accuracy, making it ideal for quick calculations.
Method 2: Estimation and Iteration (Babylonian Method)
If you don't have a calculator readily available, you can approximate the square root using an iterative method known as the Babylonian method, also called Heron's method. This method refines an initial guess through repeated calculations, converging towards the actual square root.
Steps:
-
Make an initial guess: Since 2² = 4 and 3² = 9, we know the square root of 4.25 lies between 2 and 3. Let's start with a guess of 2.1.
-
Improve the guess: Divide the number (4.25) by your initial guess (2.1) and take the average of the result and the initial guess: (4.25/2.1 + 2.1)/2 ≈ 2.0619
-
Repeat: Use the new guess (2.0619) as the input for step 2. Repeat this process until the guess converges to a desired level of accuracy. Each iteration will bring the guess closer to the actual square root.
-
Iterate until convergence: Let's do one more iteration: (4.25/2.0619 + 2.0619)/2 ≈ 2.06155
As you can see, after just a few iterations, the Babylonian method provides a very good approximation of the square root of 4.25. This method highlights the iterative nature of numerical analysis and the power of successive approximations.
Method 3: Prime Factorization and Simplification (If Applicable)
While this method isn't directly applicable to 4.25 because it's not a perfect square and doesn't easily factor into whole numbers, it's crucial to understand for other square root problems. For numbers that can be factored into perfect squares, prime factorization significantly simplifies the calculation.
For example, consider √16. The prime factorization of 16 is 2 x 2 x 2 x 2, or 2⁴. Therefore, √16 = √(2⁴) = 2². This method is particularly useful for simplifying expressions involving square roots of larger numbers.
Method 4: Using Long Division Method for Square Roots
While less common today with readily available calculators, the long division method for calculating square roots is a historical method that offers insight into the mechanics of square root computation. This method is lengthy and requires careful attention to detail but offers a strong understanding of the fundamental calculations. (A detailed explanation of this method would require a significant amount of additional space and visual representation, which is beyond the scope of this article but can be readily found online through various resources.)
Understanding the Decimal Representation: 2.06155...
The square root of 4.25, approximately 2.06155, is an irrational number. This means it cannot be expressed as a simple fraction and its decimal representation continues infinitely without repeating. The approximation 2.06155 is simply a truncated version, providing accuracy to a certain number of decimal places. The more decimal places included, the greater the accuracy of the approximation.
Application of √4.25 in Real-World Scenarios
While √4.25 might not be encountered in everyday life as frequently as other mathematical operations, it can arise in various situations involving calculations related to area, distance, or other geometric problems. For example, if you have a square with an area of 4.25 square meters, the length of each side would be √4.25 meters. Similarly, in physics or engineering, this calculation might appear in problems related to energy, motion, or other quantitative relationships.
Frequently Asked Questions (FAQ)
Q: Is √4.25 a rational or irrational number?
A: √4.25 is an irrational number. Irrational numbers are numbers that cannot be expressed as a ratio of two integers. Their decimal representations are non-terminating and non-repeating.
Q: How accurate is the approximation 2.06155?
A: The accuracy of the approximation 2.06155 depends on the context. For many purposes, this level of precision is sufficient. However, for more demanding calculations, more decimal places might be needed.
Q: Are there any online tools to calculate square roots?
A: Yes, numerous online calculators and mathematical tools can calculate square roots quickly and accurately.
Q: What is the difference between finding the square root and squaring a number?
A: Squaring a number means multiplying it by itself (e.g., 2² = 4). Finding the square root is the inverse operation; it finds the number that, when multiplied by itself, equals the original number (e.g., √4 = 2).
Conclusion: More Than Just a Calculation
The seemingly simple problem of finding the square root of 4.25 reveals a deeper appreciation for the fundamental concepts of square roots, irrational numbers, and various calculation methods. From using a calculator to the more involved iterative Babylonian method, understanding these approaches allows for a broader understanding of mathematical principles and their practical applications. Whether you're a student exploring mathematical concepts or a professional dealing with numerical analysis, grasping the nuances of this calculation enhances your mathematical toolbox and provides a deeper appreciation for the intricate beauty of numbers. The exploration of √4.25 extends beyond a simple answer; it's a journey into the world of numerical analysis and the power of approximation.
Latest Posts
Latest Posts
-
360 Ml To Oz
Sep 17, 2025
-
Tic Tac Toe Winner
Sep 17, 2025
-
Convert Grains To Grams
Sep 17, 2025
-
133 Minutes In Hours
Sep 17, 2025
-
1 3 Of 6
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 4 25 Square Root . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.