4 9 Times 2
renascent
Sep 18, 2025 · 5 min read
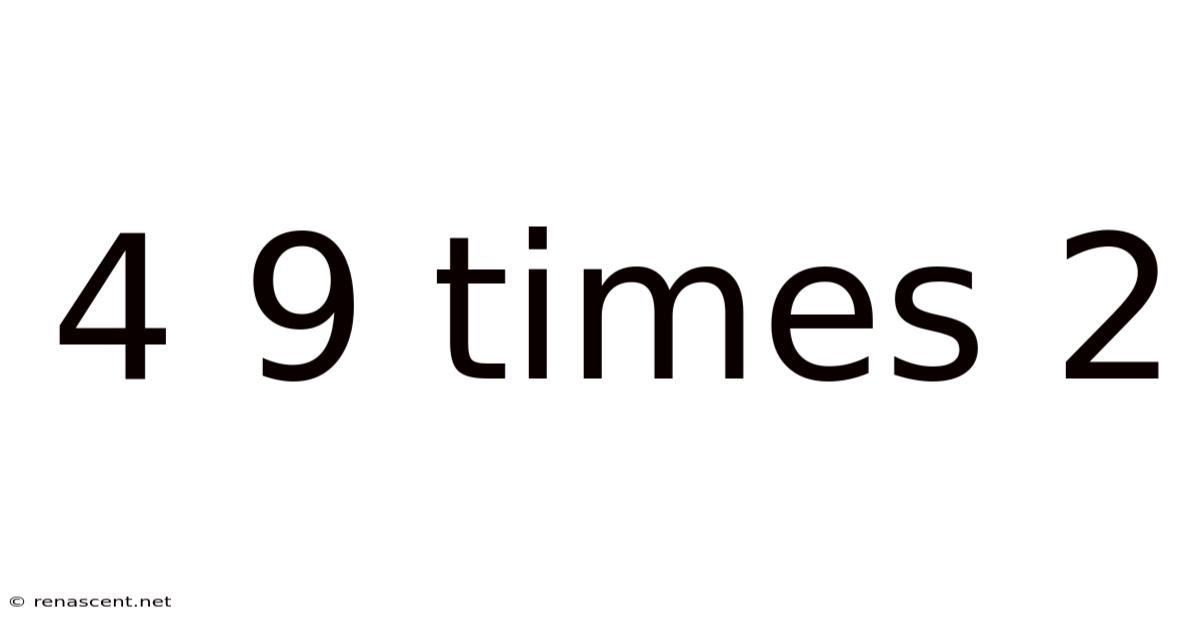
Table of Contents
Decoding 4.9 x 2: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple mathematical problem of 4.9 multiplied by 2, delving far beyond the immediate answer. We'll dissect the process, examine different approaches to solving it, explore the underlying mathematical principles, and discuss real-world applications where such calculations are essential. This comprehensive guide is designed for anyone, from elementary school students grasping the basics of multiplication to adults seeking a refresher or a deeper understanding of the subject. Understanding this simple equation unlocks a broader comprehension of mathematical operations and their relevance in everyday life.
Understanding the Fundamentals: Multiplication as Repeated Addition
At its core, multiplication is simply repeated addition. When we say 4.9 x 2, we're essentially asking: what is the sum of 4.9 added to itself twice? This basic understanding forms the foundation for tackling more complex problems. Visualizing this can be helpful, imagine two groups of 4.9 apples each – to find the total, you'd add them together: 4.9 + 4.9.
Methods for Solving 4.9 x 2
Several methods can solve this equation, each offering a slightly different approach and highlighting various mathematical concepts:
1. Direct Multiplication:
The most straightforward method is direct multiplication. We multiply 4.9 by 2:
- 2 x 9 tenths = 18 tenths = 1.8
- 2 x 4 ones = 8 ones = 8
- Adding the results: 8 + 1.8 = 9.8
Therefore, 4.9 x 2 = 9.8
2. Breaking Down the Numbers:
We can break down 4.9 into 4 + 0.9 and then multiply each part by 2 separately:
- 2 x 4 = 8
- 2 x 0.9 = 1.8
- Adding the results: 8 + 1.8 = 9.8
This method showcases the distributive property of multiplication, a fundamental concept in algebra. The distributive property states that a(b + c) = ab + ac.
3. Using Fractions:
Converting the decimal 4.9 into a fraction simplifies the multiplication:
4.9 = 49/10
Then, we multiply the fraction by 2:
(49/10) x 2 = 98/10 = 9.8
This method reinforces the connection between decimals and fractions, emphasizing the flexibility and equivalence of different mathematical representations.
4. Visual Representation:
Imagine a rectangle with a length of 4.9 units and a width of 2 units. The area of this rectangle represents the product of 4.9 and 2. Dividing the rectangle into smaller sections (e.g., a 4 x 2 rectangle and a 0.9 x 2 rectangle) visually demonstrates the breakdown method explained earlier. This approach makes the abstract concept of multiplication more concrete and easier to grasp, especially for visual learners.
The Mathematical Principles at Play
Solving 4.9 x 2 involves several fundamental mathematical principles:
-
The Commutative Property of Multiplication: This property states that the order of the numbers being multiplied does not affect the result. Therefore, 4.9 x 2 is the same as 2 x 4.9.
-
The Associative Property of Multiplication: This property allows us to group numbers differently when multiplying without changing the result. This becomes especially useful when dealing with multiple numbers.
-
The Distributive Property of Multiplication: As demonstrated earlier, this property allows us to distribute the multiplication across addition or subtraction within parentheses. This is a crucial concept in algebra and beyond.
-
Decimal Multiplication: Understanding how to multiply decimal numbers involves proper placement of the decimal point in the result, ensuring accuracy.
Real-World Applications of Decimal Multiplication
Understanding decimal multiplication like 4.9 x 2 is crucial in many real-world scenarios:
-
Shopping: Calculating the total cost of multiple items, especially when dealing with prices with decimal points (e.g., $4.99 each x 2 items).
-
Cooking and Baking: Adjusting recipes, scaling up or down ingredient quantities according to the number of servings.
-
Construction and Engineering: Precise measurements are crucial in these fields, and calculations involving decimals are fundamental for accurate estimations and design.
-
Finance and Accounting: Working with monetary amounts, calculating interest, or determining taxes often involves decimal multiplication.
-
Scientific Calculations: Many scientific formulas and measurements rely on precise decimal calculations.
-
Data Analysis: Working with datasets containing decimal values requires understanding how to perform calculations accurately.
Frequently Asked Questions (FAQ)
Q: What if I made a mistake in my calculation?
A: Double-checking your work is always crucial. Use a calculator or try a different method to verify your answer. Understanding the underlying principles will help you identify errors and correct them.
Q: How can I improve my multiplication skills?
A: Practice is key. Regularly solve multiplication problems, start with simpler ones, and gradually increase the difficulty. Use different methods to strengthen your understanding and find the approach that works best for you. Utilize online resources and educational materials for further practice and reinforcement.
Q: Are there any shortcuts for multiplying decimals?
A: While there aren’t specific shortcuts for every decimal multiplication, understanding the principles (like breaking down numbers or using fractions) can make the process more efficient. Calculators are useful tools, but understanding the underlying math remains critical.
Q: What if the problem involved more than two numbers?
A: The same principles apply. You can use the associative and commutative properties to group the numbers and multiply them systematically. For instance, 4.9 x 2 x 3 could be solved as (4.9 x 2) x 3 or 4.9 x (2 x 3).
Conclusion: Beyond the Answer
While the answer to 4.9 x 2 is simply 9.8, this article has explored the rich mathematical landscape underlying this seemingly simple calculation. We've moved beyond the mere solution to explore the fundamental principles, various methods of calculation, and the widespread practical applications of decimal multiplication in our daily lives. Mastering this basic concept builds a strong foundation for more advanced mathematical understanding and problem-solving skills applicable across numerous fields. Remember, the true value lies not just in the answer but in the journey of understanding the process itself. Keep exploring, keep questioning, and keep practicing to unlock the fascinating world of mathematics!
Latest Posts
Latest Posts
-
As Sharp As Simile
Sep 18, 2025
-
150 Seconds To Minutes
Sep 18, 2025
-
What Is 30 5
Sep 18, 2025
-
170 Kg In Pounds
Sep 18, 2025
-
Parts Of Brake Drum
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 4 9 Times 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.