4 Divided By 31
renascent
Sep 21, 2025 · 6 min read
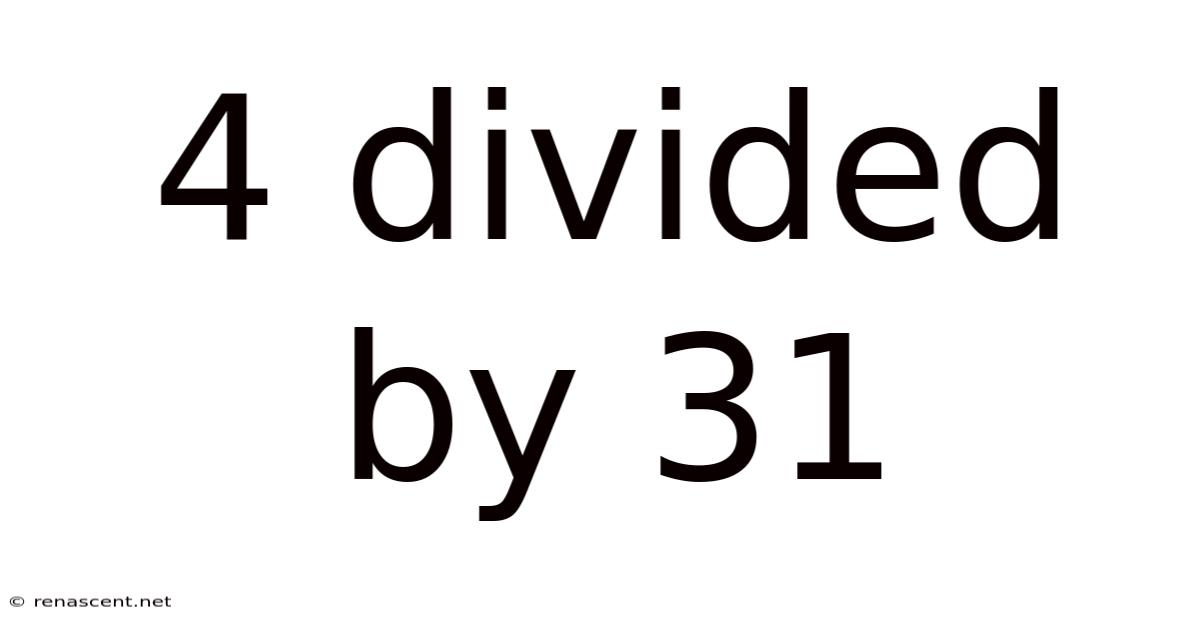
Table of Contents
Unveiling the Mystery: A Deep Dive into 4 Divided by 31
This article explores the seemingly simple calculation of 4 divided by 31, delving far beyond the immediate answer. We'll unpack the process, explore its implications within different mathematical contexts, and uncover the beauty hidden within this seemingly mundane division problem. Understanding this seemingly basic calculation lays the foundation for grasping more complex mathematical concepts. This detailed exploration will benefit students, educators, and anyone curious about the intricacies of arithmetic and its broader applications.
Understanding the Division Process
At its core, division is the inverse operation of multiplication. When we ask "what is 4 divided by 31?", we're essentially asking "what number, when multiplied by 31, equals 4?". This question immediately highlights the fact that the answer won't be a whole number. We're dealing with a fraction, a portion of a whole.
The most straightforward method is long division. Let's walk through the steps:
-
Setup: We set up the problem like this: 31 | 4
-
Initial Assessment: Since 31 is larger than 4, we know our quotient (the result of the division) will be less than 1. We'll need to add a decimal point and zeros to continue the division.
-
Adding Decimals: We rewrite the problem as: 31 | 4.0000... The addition of zeros allows us to continue the long division process.
-
Long Division: Now, we perform long division as usual. 31 doesn't go into 4, so we move to 40. 31 goes into 40 once (31 x 1 = 31), leaving a remainder of 9. We bring down the next zero.
-
Iteration: 31 goes into 90 twice (31 x 2 = 62), leaving a remainder of 28. We bring down another zero.
-
Repeating Decimal: This process will continue indefinitely. We find that 31 goes into 280 nine times (31 x 9 = 279), leaving a remainder of 1. Bringing down another zero gives us 10, and this pattern of remainders will repeat.
-
Result: The result of 4 divided by 31 is a repeating decimal, approximately 0.129032258... The sequence of digits repeats infinitely.
Representing the Result: Fractions and Decimals
The result of 4 divided by 31 can be represented in several ways:
-
Fraction: The simplest representation is the fraction 4/31. This is an irreducible fraction, meaning there's no common factor (other than 1) between the numerator (4) and the denominator (31). This fraction accurately represents the exact value.
-
Decimal: The decimal representation, 0.129032258..., is an approximation. Because the decimal repeats infinitely, we can only represent a portion of it. We often use a bar notation to indicate the repeating part, though this is not always practical. For instance, in this case, identifying the repeating block might require extended calculation, especially with larger divisors.
-
Recurring Decimal: The recurring decimal representation highlights the infinite nature of the result. The digits after the decimal point will continue to repeat in the same sequence without ever terminating. This underscores the inherent difference between rational numbers (which can be expressed as fractions) and irrational numbers (which cannot).
Exploring the Mathematical Context
This seemingly simple division problem opens doors to several important mathematical concepts:
-
Rational Numbers: The result, 4/31, is a rational number. Rational numbers are numbers that can be expressed as a fraction p/q, where p and q are integers and q is not zero. This definition perfectly encapsulates our result.
-
Irrational Numbers: While 4/31 is rational, many divisions do not result in rational numbers. For instance, the square root of 2 is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation goes on infinitely without repeating. Understanding the difference between rational and irrational numbers is crucial in higher mathematics.
-
Repeating Decimals: The repeating decimal nature of the result provides a visual representation of the concept of infinite series. We can express the repeating decimal using geometric series which is an interesting way to further understand the mathematical structure behind the result.
-
Approximations: In practical applications, we often need to approximate the value of 4/31. We might round it to a certain number of decimal places, depending on the required accuracy. This introduces the concept of error and error analysis.
-
Modular Arithmetic: The remainders generated during the long division process can be used in modular arithmetic, a branch of mathematics dealing with remainders after division. Understanding modular arithmetic is crucial in cryptography and other advanced fields.
Applications in Real-World Scenarios
While 4 divided by 31 might seem abstract, similar divisions appear in various real-world applications:
-
Portioning: Imagine dividing 4 cakes equally among 31 people. Each person receives 4/31 of a cake.
-
Measurements: In engineering or scientific measurements, we might encounter situations where dividing a small quantity by a larger one results in a small fraction, similar to our example.
-
Probability: In probability calculations, the probability of an event can often be expressed as a fraction, which might require division similar to 4/31.
-
Finance: In financial calculations, particularly when dealing with compound interest, we often encounter fractions.
-
Data Analysis: In data analysis and statistical calculations, similar division problems occur frequently, and the understanding of recurring decimal representations is critical in interpreting the resulting statistics.
Frequently Asked Questions (FAQ)
Q: Is there a simpler way to calculate 4/31 besides long division?
A: For this specific calculation, long division is perhaps the most straightforward approach. However, for more complex divisions, calculators or computer programs are typically employed.
Q: Why does the decimal representation of 4/31 repeat?
A: The decimal representation repeats because the remainder during long division eventually cycles back to a previously encountered remainder. This cyclical nature of the remainders leads to the repeating pattern in the decimal expansion. This is a characteristic of rational numbers.
Q: How accurate is the decimal approximation of 4/31?
A: The accuracy of the approximation depends on the number of decimal places used. The more decimal places we include, the more accurate the approximation becomes. However, it will always be an approximation, as the true value is an infinitely repeating decimal.
Q: Can 4/31 be simplified further?
A: No, 4/31 is already in its simplest form because 4 and 31 do not share any common factors other than 1.
Q: What are some practical applications of understanding this type of calculation?
A: Understanding how to perform such a division, and interpreting the resulting fraction or repeating decimal, is crucial for various applications, such as those discussed in the "Applications" section above, and is fundamental to a deeper comprehension of mathematics and its role in our world.
Conclusion
The seemingly simple calculation of 4 divided by 31 offers a surprising depth of mathematical insight. From understanding rational numbers and their decimal representations to grasping the concept of repeating decimals and infinite series, this problem serves as a microcosm of broader mathematical concepts. By understanding the process, its representation, and its implications, we deepen our appreciation for the elegance and intricacy of mathematics and its pervasive influence across various fields of study and everyday life. The seemingly mundane act of division reveals a world of fascinating mathematical properties, illustrating that even the simplest calculations can unlock a wealth of understanding.
Latest Posts
Latest Posts
-
13 20 As A Percent
Sep 21, 2025
-
Barium Sulfate Molar Mass
Sep 21, 2025
-
Polynomial Long Division Calc
Sep 21, 2025
-
Benefits Of Asexual Reproduction
Sep 21, 2025
-
B And D Plumbing
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 4 Divided By 31 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.