4 Divided By 37
renascent
Sep 21, 2025 · 4 min read
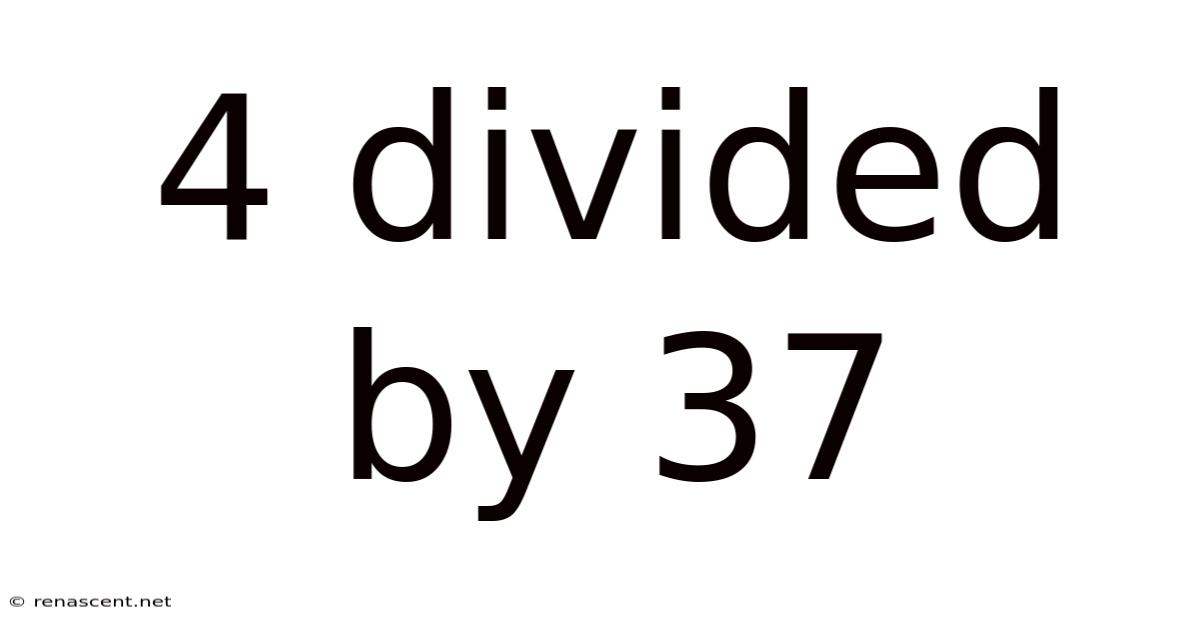
Table of Contents
Diving Deep into 4 Divided by 37: A Journey into Division and Decimal Representation
This article explores the seemingly simple calculation of 4 divided by 37, delving beyond the immediate answer to uncover the underlying mathematical concepts and practical applications. We'll unpack the process of long division, explore the nature of repeating decimals, and discuss the significance of this seemingly mundane calculation in broader mathematical contexts. Understanding this seemingly simple division problem provides a strong foundation for grasping more complex mathematical concepts.
Understanding the Problem: 4 ÷ 37
The core question is: What is the result of dividing 4 by 37? At first glance, it might seem straightforward, but the answer reveals fascinating insights into the world of decimal representation and the limitations of expressing certain fractions as terminating decimals. This calculation highlights the difference between rational and irrational numbers, a fundamental distinction in mathematics.
Performing Long Division: A Step-by-Step Approach
Let's perform the long division manually to understand the process. Remember, the goal is to find how many times 37 goes into 4. Since 37 is larger than 4, we'll need to add a decimal point and zeros to the dividend (4).
-
Setup: Write 4 as 4.0000... (adding as many zeros as needed for accuracy). Set up your long division problem with 37 as the divisor and 4.0000... as the dividend.
-
Initial Division: 37 does not go into 4, so we place a zero above the 4 and proceed to the tenths place.
-
Bringing Down Zeros: Bring down a zero to make it 40. 37 goes into 40 once (37 x 1 = 37). Write '1' above the first zero in the quotient.
-
Subtraction and Remainder: Subtract 37 from 40, leaving a remainder of 3.
-
Repeating the Process: Bring down another zero to make it 30. 37 does not go into 30, so we write a '0' above the next zero in the quotient. Bring down another zero to make it 300.
-
Finding the Pattern: 37 goes into 300 eight times (37 x 8 = 296). Write '8' above the third zero in the quotient. Subtract 296 from 300, leaving a remainder of 4.
-
The Repeating Decimal: Notice that we are now back to a remainder of 4, the same as our starting point. This indicates that the decimal representation will repeat infinitely.
-
Final Result: The result of 4 ÷ 37 is approximately 0.108108108... The sequence "108" repeats infinitely. We represent this using a bar notation: 0.$\overline{108}$.
Understanding Repeating Decimals: Rational Numbers
The result, 0.$\overline{108}$, is a repeating decimal or a recurring decimal. This is characteristic of rational numbers. A rational number is a number that can be expressed as a fraction p/q, where p and q are integers, and q is not zero. In this case, 4/37 is a rational number because both 4 and 37 are integers. The repeating decimal pattern is a consequence of the fact that the long division process never reaches a zero remainder.
Implications and Applications
While this specific calculation might seem trivial, understanding the principles behind it has significant implications:
-
Understanding Fractions and Decimals: It reinforces the relationship between fractions and decimal representations. Not all fractions have terminating decimal equivalents.
-
Computer Programming: Representing and working with repeating decimals in computer programs requires careful consideration. Due to the finite precision of computers, rounding errors can occur when dealing with infinite repeating decimals. Algorithms and techniques are needed to handle these limitations effectively.
-
Advanced Mathematics: The concept of repeating decimals forms the basis for understanding continued fractions and other advanced mathematical concepts.
-
Real-world Applications: Though not directly visible, this understanding of decimal representation underpins calculations in various fields, including engineering, finance, and physics, where precise measurements and calculations are essential.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this?
A: Yes, a calculator will give you an approximate answer, usually displaying a truncated version of the repeating decimal. However, the calculator might not explicitly show the repeating nature of the decimal.
Q: Why does the decimal repeat?
A: The decimal repeats because when performing long division, the remainder keeps cycling back to a previous value. This creates a loop in the division process, resulting in a repeating pattern in the quotient.
Q: Is there a way to express 4/37 without using a repeating decimal?
A: No, there isn't a way to express 4/37 as a terminating decimal. The fraction itself is the most precise representation.
Conclusion: Beyond the Numbers
The seemingly simple calculation of 4 divided by 37 offers a valuable opportunity to explore fundamental mathematical concepts. It reveals the intricacies of decimal representation, highlights the distinction between rational and irrational numbers, and demonstrates the importance of understanding the underlying mathematical principles behind seemingly simple calculations. The process of long division, while seemingly tedious, provides a concrete understanding of how repeating decimals arise and why they are an essential part of the mathematical landscape. This seemingly simple problem underscores the power of mathematics to unveil hidden patterns and structures within numbers. By understanding the 'why' behind the calculation, we build a stronger mathematical foundation for future learning and application.
Latest Posts
Latest Posts
-
120 Yards In Meters
Sep 21, 2025
-
5 8 2 3
Sep 21, 2025
-
6 Tablespoons In Ounces
Sep 21, 2025
-
99 Pounds To Kg
Sep 21, 2025
-
56 F In C
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 4 Divided By 37 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.