40 Divided By 10
renascent
Sep 21, 2025 · 6 min read
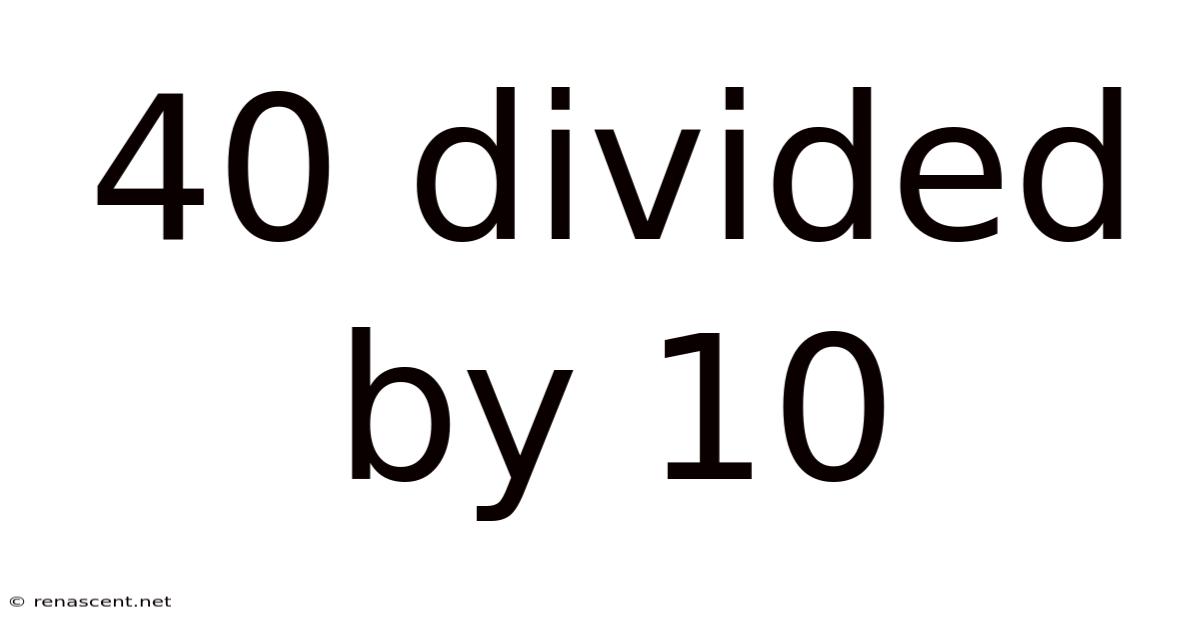
Table of Contents
40 Divided by 10: A Deep Dive into Division and its Applications
This article explores the seemingly simple calculation of 40 divided by 10, delving beyond the immediate answer to uncover the fundamental principles of division, its real-world applications, and its significance in mathematics and beyond. Understanding division is crucial for various aspects of life, from everyday budgeting to complex scientific calculations. This exploration will cover the basic concept, different methods of solving the problem, practical examples, and frequently asked questions. By the end, you'll not only know that 40 divided by 10 equals 4, but also understand the underlying mathematical concepts and their broader implications.
Introduction: Understanding Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It's essentially the process of splitting a whole number into equal parts. In the equation 40 ÷ 10 = ?, we are asking: "How many times does 10 go into 40?" or "If we divide 40 into groups of 10, how many groups will we have?" The answer, as we'll soon demonstrate through various methods, is 4. This seemingly simple calculation forms the bedrock for understanding more complex mathematical concepts.
Method 1: Repeated Subtraction
One way to visualize 40 ÷ 10 is through repeated subtraction. We can repeatedly subtract 10 from 40 until we reach zero.
- 40 - 10 = 30
- 30 - 10 = 20
- 20 - 10 = 10
- 10 - 10 = 0
We subtracted 10 four times to reach zero. Therefore, 40 ÷ 10 = 4. This method is particularly helpful for understanding the concept of division, especially for younger learners who can visualize the process of taking away equal groups.
Method 2: Using Multiplication Facts
Division and multiplication are inverse operations. This means that if we know the multiplication facts, we can easily solve division problems. We're looking for a number that, when multiplied by 10, equals 40. Since 10 x 4 = 40, then 40 ÷ 10 = 4. This method leverages the familiarity of multiplication tables, making it a quick and efficient way to solve simple division problems.
Method 3: Long Division
While long division might seem excessive for such a simple problem, it's crucial to understand the process for tackling more complex division problems. Here's how you would perform long division for 40 ÷ 10:
4
10 | 40
-40
--
0
10 goes into 40 four times (10 x 4 = 40). Subtracting 40 from 40 leaves a remainder of 0, indicating that the division is exact. Long division provides a structured approach that can be applied to more challenging divisions with larger numbers and remainders.
Real-World Applications of Division: Beyond the Classroom
The concept of division is far from a theoretical exercise; it's deeply embedded in our daily lives. Consider these examples:
-
Sharing Equally: Imagine you have 40 candies to share equally among 10 friends. Division helps you determine that each friend receives 4 candies (40 ÷ 10 = 4).
-
Calculating Unit Price: If a pack of 10 pencils costs $40, the unit price (cost per pencil) is found by dividing the total cost by the number of pencils: $40 ÷ 10 = $4 per pencil.
-
Measuring and Cutting: A carpenter needs to cut a 40-meter long plank of wood into 10 equal pieces. Division helps determine that each piece will be 4 meters long (40 ÷ 10 = 4).
-
Budgeting and Finance: If you have $40 to spend on 10 items, you can use division to find out how much you can spend on each item: $40 ÷ 10 = $4 per item.
-
Data Analysis and Statistics: Division is fundamental in calculating averages, rates, and proportions in various data analysis scenarios. For example, if you have 40 data points and want to divide them into 10 equal groups for analysis, you would use division.
-
Scientific Applications: From calculating speeds and distances in physics to determining concentrations in chemistry, division is a core tool in scientific calculations and problem-solving.
Expanding the Concept: Division with Remainders
While 40 ÷ 10 results in a clean division with no remainder, it's important to understand how to handle scenarios with remainders. Consider the example of 43 ÷ 10.
10 goes into 43 four times (10 x 4 = 40), with a remainder of 3 (43 - 40 = 3). This can be expressed as 4 with a remainder of 3, or as a mixed number (4 3/10), or as a decimal (4.3). Understanding how to handle remainders is crucial for solving more complex division problems.
Division and Fractions: A Deeper Connection
Division and fractions are closely related. The expression 40 ÷ 10 can also be written as the fraction 40/10. Simplifying this fraction by dividing both the numerator and the denominator by their greatest common divisor (10) gives us 4/1, which is equal to 4. This highlights the interconnectedness of different mathematical concepts.
Division in Different Number Systems
While we've focused on the decimal system (base 10), division applies to other number systems as well, such as binary (base 2) used in computer science. The principles remain the same, although the representation of numbers and the calculations might look different.
Exploring Larger Numbers: Scaling Up the Problem
Let's consider a larger, but conceptually similar problem: 400 ÷ 10. Using the same principles, we can quickly determine that 400 ÷ 10 = 40. Notice that we've simply added a zero to the answer. This demonstrates how understanding the basic principle of division allows us to efficiently solve more complex problems. Similarly, 4000 ÷ 10 = 400 and so on. This pattern highlights the relationship between the number of zeros in the dividend and the quotient.
Advanced Concepts Related to Division
While this article primarily focuses on the basics, it's worth mentioning some advanced concepts connected to division:
-
Euclidean Division: This theorem provides a formal framework for division with remainders, particularly useful in number theory.
-
Modular Arithmetic: This system uses remainders after division to define equivalence classes and perform operations within those classes.
-
Polynomial Division: This extends the concept of division to polynomials (expressions with variables and exponents).
Frequently Asked Questions (FAQs)
-
What is the dividend in 40 ÷ 10? The dividend is 40, the number being divided.
-
What is the divisor in 40 ÷ 10? The divisor is 10, the number we are dividing by.
-
What is the quotient in 40 ÷ 10? The quotient is 4, the result of the division.
-
What is the remainder in 40 ÷ 10? The remainder is 0, because the division is exact.
-
Can division be performed on decimals? Yes, division applies to decimal numbers as well.
-
What happens when you divide by zero? Dividing by zero is undefined in mathematics. It's not a valid operation.
Conclusion: The Power of Division
This comprehensive exploration of 40 divided by 10 reveals that this seemingly simple calculation is a gateway to understanding fundamental mathematical principles and their wide-ranging applications. From everyday tasks to complex scientific calculations, division is a crucial tool. By mastering the concepts presented here, you'll be better equipped to tackle more complex mathematical problems and understand the world around you more effectively. The ability to divide efficiently and accurately is a valuable skill that extends far beyond the classroom and into all aspects of life. Remember, while the answer to 40 divided by 10 is 4, the true value lies in grasping the underlying concepts and their significance.
Latest Posts
Latest Posts
-
52 5 Kg In Lbs
Sep 21, 2025
-
1 4 Of 20
Sep 21, 2025
-
80 5 Kg In Pounds
Sep 21, 2025
-
166 Min To Hours
Sep 21, 2025
-
Rudy In Ice Age
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 40 Divided By 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.