40 Percent Of 250
renascent
Sep 24, 2025 · 5 min read
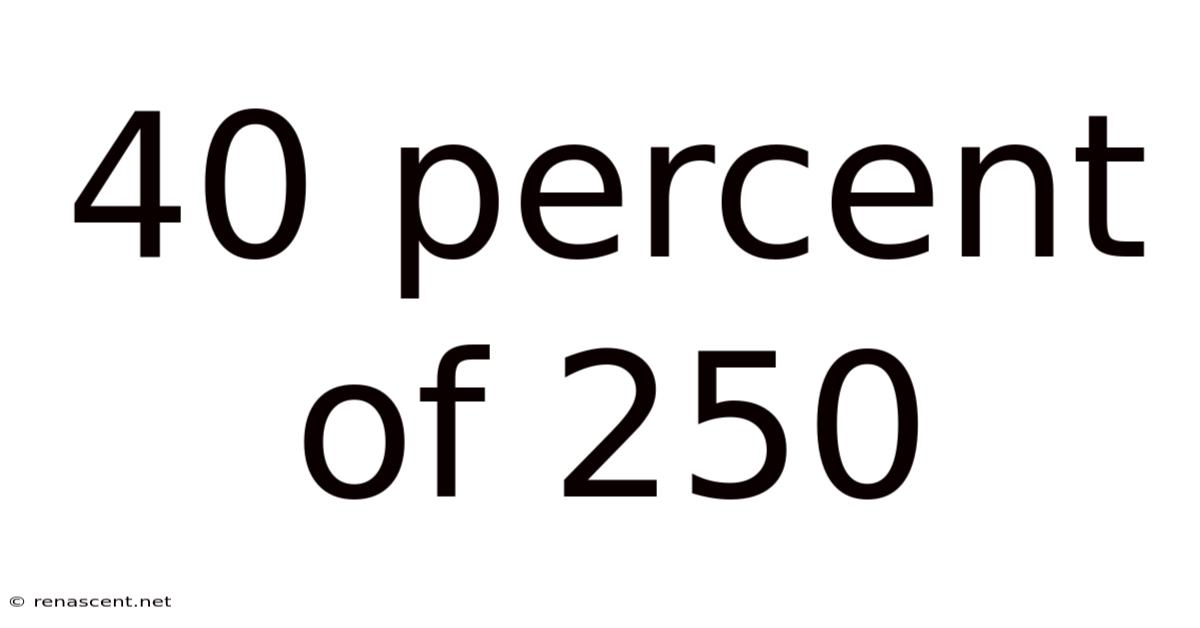
Table of Contents
Unveiling the Mystery: Calculating 40% of 250 and Beyond
Finding 40% of 250 might seem like a simple arithmetic problem, but it's a gateway to understanding percentages, a fundamental concept in mathematics with widespread applications in everyday life, from calculating discounts and taxes to understanding statistics and financial data. This article will not only show you how to calculate 40% of 250 using various methods but also delve deeper into the underlying principles, providing you with a robust understanding of percentages and their practical implications. We'll explore different approaches, tackle common misconceptions, and even address some frequently asked questions. By the end, you'll be confident in tackling percentage calculations of any kind.
Understanding Percentages: The Foundation
Before diving into the calculation, let's establish a firm understanding of what percentages represent. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." So, 40% means 40 out of 100, which can be written as the fraction 40/100 or the decimal 0.40. This fundamental understanding is crucial for all percentage calculations.
Method 1: The Fraction Method
This is arguably the most intuitive method for calculating percentages, especially for those who are comfortable working with fractions. We start by converting the percentage into a fraction:
-
Convert the percentage to a fraction: 40% is equal to 40/100.
-
Simplify the fraction (optional): We can simplify 40/100 by dividing both the numerator and denominator by their greatest common divisor, which is 20. This simplifies to 2/5.
-
Multiply the fraction by the whole number: Now, we multiply the simplified fraction (2/5) by 250: (2/5) * 250 = 100
Therefore, 40% of 250 is 100.
Method 2: The Decimal Method
The decimal method involves converting the percentage into a decimal and then multiplying it by the whole number. This is often the preferred method for those who are comfortable with decimal calculations:
-
Convert the percentage to a decimal: 40% is equal to 0.40 (or simply 0.4).
-
Multiply the decimal by the whole number: Multiply 0.4 by 250: 0.4 * 250 = 100
Again, we find that 40% of 250 is 100.
Method 3: Using Proportions
This method utilizes the concept of proportions, setting up an equation to solve for the unknown value. This method is particularly useful for understanding the underlying relationships between percentages and whole numbers:
-
Set up a proportion: We can set up a proportion as follows:
x / 250 = 40 / 100
where 'x' represents the unknown value (40% of 250).
-
Cross-multiply: Cross-multiplying gives us:
100x = 40 * 250
-
Solve for x: This simplifies to:
100x = 10000
x = 10000 / 100
x = 100
Thus, using the proportion method, we confirm that 40% of 250 is 100.
Method 4: The Percentage Formula
A more formal approach involves using the percentage formula:
Percentage = (Part / Whole) * 100
In our case, we know the percentage (40%) and the whole (250), and we need to find the part. We can rearrange the formula to solve for the part:
Part = (Percentage / 100) * Whole
Substituting the values:
Part = (40 / 100) * 250 = 100
This method reinforces the fundamental relationship between percentages, parts, and wholes.
Real-World Applications: Beyond the Calculation
Understanding how to calculate 40% of 250 extends far beyond simple arithmetic exercises. Let's explore some real-world scenarios where this type of calculation is vital:
-
Sales and Discounts: Imagine a store offering a 40% discount on an item priced at $250. Using our calculation, the discount amount would be $100, making the final price $150.
-
Taxes and Fees: If a 40% tax is levied on a $250 purchase, the tax amount would be $100, resulting in a total cost of $350.
-
Statistics and Data Analysis: Percentages are frequently used to represent proportions in datasets. For example, if a survey of 250 people shows that 40% prefer a particular brand, this means 100 people prefer that brand.
-
Financial Calculations: From calculating interest rates on loans to understanding investment returns, percentage calculations are fundamental in finance.
-
Scientific Calculations: Many scientific calculations involve determining percentages, for example, when analyzing experimental data or determining concentrations of solutions.
Common Mistakes to Avoid
While percentage calculations are relatively straightforward, there are common pitfalls to watch out for:
-
Incorrect Decimal Conversion: Ensure you accurately convert percentages to decimals before multiplying. A simple mistake here can lead to a significantly incorrect answer.
-
Misinterpreting the Question: Carefully read the problem statement to understand what is being asked. Are you calculating the percentage of a number, or are you working with a different aspect of a percentage-related problem?
-
Calculation Errors: Double-check your calculations to avoid simple arithmetic mistakes. Using a calculator can help minimize these errors.
Frequently Asked Questions (FAQ)
Q1: How can I calculate a different percentage of 250?
A1: You can use any of the methods described above, simply replacing 40% with the desired percentage. For example, to calculate 25% of 250, you would substitute 25/100 or 0.25 into the equation.
Q2: What if I need to calculate the percentage one number represents of another?
A2: Use the percentage formula: Percentage = (Part / Whole) * 100. For example, if 100 is a part of 250, the percentage would be (100/250)*100 = 40%.
Q3: Are there online calculators for percentage calculations?
A3: Yes, many online calculators can quickly compute percentages. However, understanding the underlying principles is crucial for applying this knowledge effectively in diverse situations.
Q4: Can I use a spreadsheet program like Excel or Google Sheets to calculate percentages?
A4: Absolutely! Spreadsheet programs are powerful tools for performing percentage calculations, particularly when dealing with large datasets or complex calculations.
Conclusion: Mastering Percentages for a Brighter Future
Calculating 40% of 250, while seemingly simple, opens the door to a deeper understanding of percentages and their wide-ranging applications. By mastering various calculation methods and understanding the underlying principles, you equip yourself with a valuable skill applicable across numerous fields. Whether it's navigating discounts in a store, understanding financial statements, or analyzing data, the ability to work confidently with percentages is a skill that will serve you well throughout your life. Remember to practice regularly and don't hesitate to explore different approaches to find the method that works best for you. The key is not just to get the answer but to grasp the why behind the calculation.
Latest Posts
Latest Posts
-
Formula For Vertical Exaggeration
Sep 24, 2025
-
Bi Annual Versus Biennial
Sep 24, 2025
-
84 5 Kg To Lbs
Sep 24, 2025
-
100 Ounces To Ml
Sep 24, 2025
-
225 Mph To Kmh
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 40 Percent Of 250 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.