400 Divided By 12
renascent
Sep 23, 2025 · 6 min read
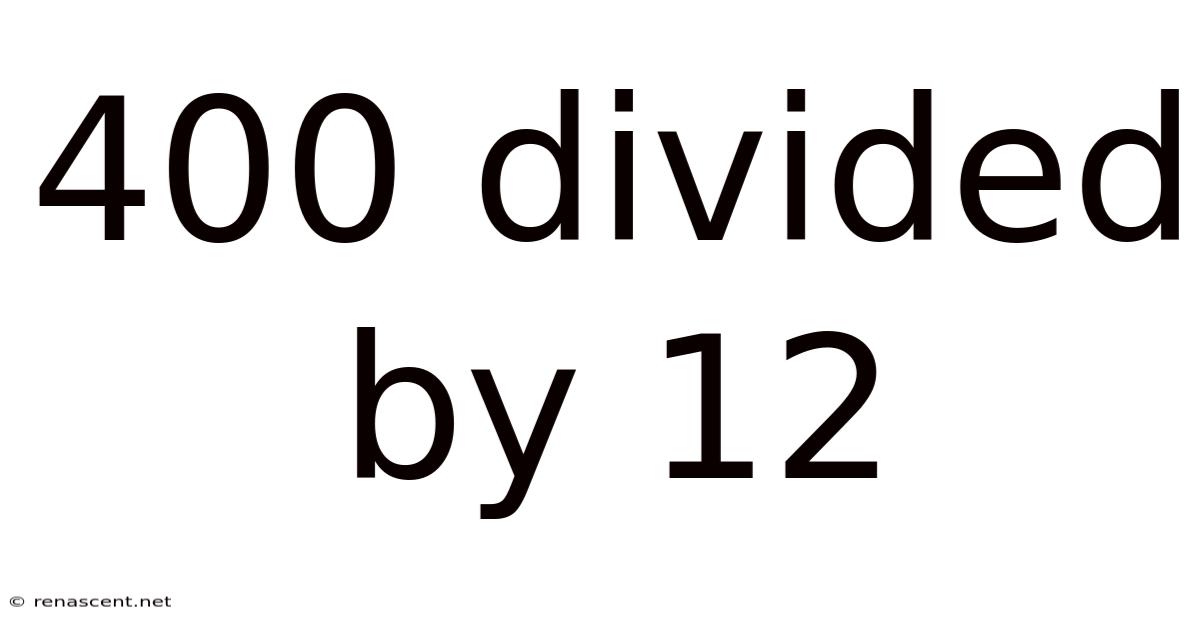
Table of Contents
Unveiling the Mystery: 400 Divided by 12 – A Deep Dive into Division
The seemingly simple question, "What is 400 divided by 12?", opens a door to a world of mathematical concepts, problem-solving strategies, and practical applications. This article will not only answer this question definitively but will also explore the underlying principles of division, different methods for solving the problem, and real-world scenarios where such calculations are essential. We'll journey from basic arithmetic to more advanced concepts, ensuring a comprehensive understanding for learners of all levels.
Understanding Division: The Basics
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a whole quantity into equal parts. In the equation 400 ÷ 12, we are asking: "How many times does 12 fit into 400?" The answer to this question will be a quotient (the result of the division), potentially accompanied by a remainder (any leftover amount that cannot be evenly divided).
Understanding the components is crucial:
- Dividend: The number being divided (400 in this case).
- Divisor: The number by which we are dividing (12 in this case).
- Quotient: The result of the division.
- Remainder: The amount left over after the division (if any).
Method 1: Long Division
Long division is a classic method, particularly useful for larger numbers where mental calculation becomes challenging. Let's work through 400 ÷ 12 step-by-step:
-
Set up the problem: Write 400 inside the long division symbol (⟌) with 12 outside.
-
Divide the tens: 12 goes into 40 three times (12 x 3 = 36). Write "3" above the "0" in 400.
-
Subtract: Subtract 36 from 40, leaving 4.
-
Bring down the ones: Bring down the "0" from 400, giving you 40.
-
Divide again: 12 goes into 40 three times (12 x 3 = 36). Write "3" above the "0" in 400 (next to the 3 you already wrote).
-
Subtract again: Subtract 36 from 40, leaving 4.
-
Remainder: The remainder is 4.
Therefore, 400 ÷ 12 = 33 with a remainder of 4.
Method 2: Repeated Subtraction
This method is conceptually simpler, especially for beginners. We repeatedly subtract the divisor (12) from the dividend (400) until we can no longer subtract without going negative. The number of times we subtract is the quotient. Let's demonstrate:
- Start with 400: 400 - 12 = 388
- Subtract again: 388 - 12 = 376
- Continue subtracting: Repeating this process will eventually lead you to a number less than 12. Counting how many times you subtracted 12 will yield the quotient.
This method is time-consuming for larger numbers but provides a strong intuitive understanding of division. While it won’t give the same efficient result as long division for 400/12, it’s beneficial for grasping the core concept.
Method 3: Using Fractions
Division can be expressed as a fraction. 400 ÷ 12 is the same as 400/12. We can simplify this fraction by finding the greatest common divisor (GCD) of 400 and 12, which is 4. Dividing both the numerator and denominator by 4 simplifies the fraction to 100/3. This is an improper fraction (the numerator is larger than the denominator).
To convert this improper fraction to a mixed number (a whole number and a fraction), we divide 100 by 3:
100 ÷ 3 = 33 with a remainder of 1.
Therefore, 100/3 = 33 1/3. This confirms our earlier result, showing that 400 ÷ 12 equals 33 with a remainder of 4, or expressed as a mixed number, 33 and 1/3.
Method 4: Using a Calculator
For practical purposes, especially in situations requiring speed and accuracy, a calculator provides the quickest solution. Simply input 400 ÷ 12 and the calculator will immediately display the result: 33.3333... The repeating decimal indicates the fractional part (1/3).
Real-World Applications
The ability to perform division, and specifically to solve problems like 400 ÷ 12, is vital in numerous real-world scenarios:
-
Resource Allocation: Imagine you have 400 cookies to distribute equally among 12 classrooms. Dividing 400 by 12 tells you each classroom receives 33 cookies, with 4 cookies left over.
-
Financial Calculations: Dividing a total budget among several projects, calculating unit costs, or determining average earnings all involve division.
-
Measurement and Conversions: Converting units of measurement, such as inches to feet or kilograms to pounds, often requires division.
-
Engineering and Construction: Calculating material quantities, dividing areas into sections, or determining proportions in building designs all rely on division.
-
Data Analysis: Calculating averages, percentages, and ratios in data analysis heavily depends on the ability to perform division accurately.
Exploring Further: Decimals and Fractions
Understanding the relationship between decimals and fractions is crucial when dealing with division problems that don't result in a whole number. As shown above, 400/12 can be expressed as the mixed number 33 1/3 or the repeating decimal 33.333... This highlights the importance of understanding different representations of numbers. The decimal representation is convenient for many applications, especially when working with calculators or computers. However, fractions often provide a more precise and exact representation, especially when dealing with repeated decimals.
Frequently Asked Questions (FAQ)
Q: What is the difference between a quotient and a remainder?
A: The quotient is the whole number result of the division. The remainder is the amount left over after dividing as evenly as possible.
Q: Can I use a different method to solve 400 ÷ 12?
A: Yes, various methods exist, including long division, repeated subtraction, using fractions, and employing a calculator. The best method depends on your comfort level, the complexity of the problem, and the desired level of precision.
Q: Why is the decimal representation of 400 ÷ 12 a repeating decimal?
A: The repeating decimal arises because the fraction 1/3 cannot be represented exactly as a terminating decimal. It's a rational number, but its decimal form goes on infinitely.
Q: What if I need to divide 400 by a number other than 12?
A: The same principles and methods apply. You would simply replace 12 with the new divisor and follow the chosen method to find the quotient and remainder.
Conclusion: Mastering Division and Beyond
Solving 400 divided by 12 is more than just a simple arithmetic problem. It's a gateway to understanding the fundamental principles of division, exploring different problem-solving techniques, and appreciating the numerous real-world applications of this essential mathematical operation. Whether you use long division, repeated subtraction, fractions, or a calculator, the process reinforces fundamental mathematical skills and provides a stepping stone to more advanced mathematical concepts. By understanding the nuances of division, you equip yourself with a valuable tool for tackling complex challenges in various fields. Remember that mathematical fluency is built not just through rote memorization, but through a deep understanding of the underlying concepts and their practical applications.
Latest Posts
Latest Posts
-
Ancient Greek Drama Costumes
Sep 23, 2025
-
Food Web Cane Toad
Sep 23, 2025
-
Unity Meaning In Art
Sep 23, 2025
-
Descriptive Words About Summer
Sep 23, 2025
-
4 Meters In Inches
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 400 Divided By 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.