42 Divided By 4
renascent
Sep 24, 2025 · 7 min read
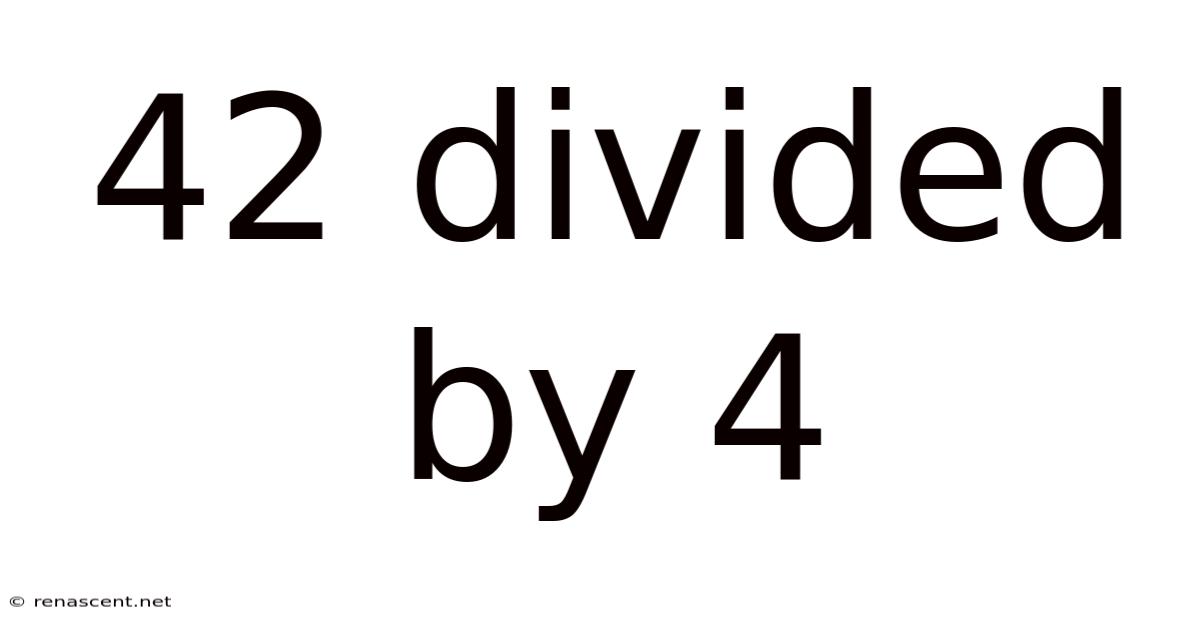
Table of Contents
Unveiling the Mystery: A Deep Dive into 42 Divided by 4
Dividing 42 by 4 might seem like a simple arithmetic problem, suitable only for elementary school students. However, a closer examination reveals a wealth of mathematical concepts and practical applications that extend far beyond a basic calculation. This comprehensive exploration delves into the intricacies of this seemingly straightforward division problem, covering various methods of solution, exploring the underlying mathematical principles, and showcasing its relevance in real-world scenarios. Understanding this seemingly simple calculation provides a solid foundation for more advanced mathematical concepts.
Understanding Division: A Foundational Concept
Before tackling 42 divided by 4, let's refresh our understanding of division itself. Division is essentially the inverse operation of multiplication. While multiplication combines groups of equal size, division separates a quantity into equal groups or determines how many times one quantity is contained within another. In the context of 42 divided by 4, we're asking: "How many times does 4 go into 42?" or "If we divide 42 into 4 equal groups, how many will be in each group?"
Method 1: Long Division – The Classic Approach
Long division is a tried-and-true method for tackling division problems, especially those involving larger numbers. Let's walk through the process step-by-step:
-
Set up the problem: Write the dividend (42) inside the long division symbol (÷) and the divisor (4) outside.
4 | 42 -
Divide the tens digit: How many times does 4 go into 4 (the tens digit of 42)? The answer is 1. Write the 1 above the 4 in the quotient.
1 4 | 42 -
Multiply and subtract: Multiply the quotient digit (1) by the divisor (4): 1 x 4 = 4. Subtract this result from the tens digit of the dividend (4 - 4 = 0).
1 4 | 42 -4 -- 0 -
Bring down the ones digit: Bring down the ones digit of the dividend (2) next to the 0.
1 4 | 42 -4 -- 02 -
Divide the ones digit: How many times does 4 go into 2? It goes 0 times. Write 0 above the 2 in the quotient.
10 4 | 42 -4 -- 02 -
Multiply and subtract: Multiply the new quotient digit (0) by the divisor (4): 0 x 4 = 0. Subtract this from the remaining digit (2 - 0 = 2). This is the remainder.
10 4 | 42 -4 -- 02 -0 -- 2
Therefore, 42 divided by 4 is 10 with a remainder of 2. We can express this as 10 R 2 or 10 2/4, which simplifies to 10 ½.
Method 2: Repeated Subtraction – A Visual Approach
Repeated subtraction offers a more visual understanding of division. It involves subtracting the divisor repeatedly from the dividend until the result is less than the divisor. The number of times we subtract represents the quotient, and the remaining number is the remainder.
Let's apply this to 42 divided by 4:
-
Start with the dividend: 42
-
Subtract the divisor repeatedly:
- 42 - 4 = 38
- 38 - 4 = 34
- 34 - 4 = 30
- 30 - 4 = 26
- 26 - 4 = 22
- 22 - 4 = 18
- 18 - 4 = 14
- 14 - 4 = 10
- 10 - 4 = 6
- 6 - 4 = 2
-
Count the subtractions: We subtracted 4 ten times. This is our quotient.
-
The remainder: The remaining number after the last subtraction is 2.
Therefore, again, we find that 42 divided by 4 is 10 with a remainder of 2 (10 R 2 or 10 ½).
Method 3: Using Fractions – A Deeper Understanding
Division can also be represented as a fraction. In this case, 42 divided by 4 can be written as 42/4. This fraction can be simplified:
-
Find common factors: Both 42 and 4 are divisible by 2.
-
Simplify: 42/4 = (21 x 2) / (2 x 2) = 21/2
-
Convert to mixed number: 21 divided by 2 is 10 with a remainder of 1. This can be expressed as 10 1/2.
This method reinforces the equivalence between division and fractions, highlighting that the result (10 ½) remains consistent regardless of the method used.
Decimal Representation – Extending Precision
While the remainder of 2 provides a complete answer, we can express the result as a decimal for greater precision. To do this, we continue the long division process beyond the remainder:
-
Add a decimal point and a zero: After obtaining the remainder 2, add a decimal point to the quotient (10.) and a zero to the remainder (20).
-
Continue the division: How many times does 4 go into 20? Five times. Add 5 to the quotient.
10.5 4 | 42.0 -4 -- 02 -0 -- 20 -20 -- 0
Therefore, 42 divided by 4 is 10.5. This decimal representation provides a more precise answer, particularly useful in situations requiring decimal accuracy.
Real-World Applications – Beyond the Textbook
The division of 42 by 4 isn't merely an abstract mathematical exercise; it has practical applications in numerous real-world scenarios:
-
Sharing resources: Imagine you have 42 candies to share equally among 4 friends. Each friend would receive 10 candies, and you'd have 2 candies left over.
-
Calculating unit costs: If 42 meters of fabric costs $4, the cost per meter is $4 / 42 meters = approximately $0.095 per meter (calculated using a decimal representation).
-
Measuring quantities: Imagine you need to divide a 42-inch piece of wood into 4 equal sections. Each section would be 10.5 inches long.
-
Averaging values: If four test scores total 42 points, the average score is 10.5 points.
These examples demonstrate that the concept of division, even in a simple problem like 42 divided by 4, is essential for solving practical problems in various fields.
Addressing Common Misconceptions
A common misunderstanding surrounding division with remainders is interpreting the remainder as insignificant. The remainder provides crucial information, often representing leftover quantities or fractional parts. Ignoring the remainder can lead to inaccurate results in real-world applications. For example, in the candy sharing scenario, ignoring the remainder of 2 would mean two friends receive one candy less than the others.
Frequently Asked Questions (FAQ)
Q: What is the most efficient method for dividing 42 by 4?
A: The most efficient method depends on the context and personal preference. For quick mental calculation, repeated subtraction might be useful. For more complex problems or situations requiring decimal precision, long division is generally preferred.
Q: Why is the result sometimes expressed as a mixed number (10 ½) and sometimes as a decimal (10.5)?
A: Both representations are correct and equivalent. The choice depends on the required level of precision and the context of the problem. A mixed number is appropriate when dealing with whole units and leftover parts, while a decimal is more suitable for situations requiring precise numerical values.
Q: Can the remainder be expressed as a fraction?
A: Absolutely! The remainder (2) can be expressed as a fraction over the divisor (4), resulting in the fraction 2/4, which simplifies to 1/2. This is why we can represent the answer as 10 ½, which is equivalent to 10.5.
Q: What happens if the divisor is larger than the dividend?
A: If the divisor is larger than the dividend, the quotient will be 0, and the remainder will be the dividend itself. For example, 4 divided by 42 would be 0 with a remainder of 4.
Conclusion: A Simple Problem, Profound Implications
While the division of 42 by 4 might appear deceptively simple at first glance, a thorough examination reveals a rich tapestry of mathematical concepts and practical applications. Mastering this seemingly basic calculation lays a strong foundation for tackling more complex problems and understanding the real-world relevance of mathematical operations. From the classic long division method to the visual approach of repeated subtraction and the fractional representation, various approaches highlight the flexibility and power of division as a fundamental tool in mathematics. Remember, the seemingly simple problems often hold the keys to unlocking a deeper understanding of the broader mathematical landscape.
Latest Posts
Latest Posts
-
What Is 25 25
Sep 24, 2025
-
6 5 5 6
Sep 24, 2025
-
Signs Of Secure Attachment
Sep 24, 2025
-
Number Line To 10
Sep 24, 2025
-
18 Km Per Hour
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 42 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.