45 Divided By 2
renascent
Sep 24, 2025 · 5 min read
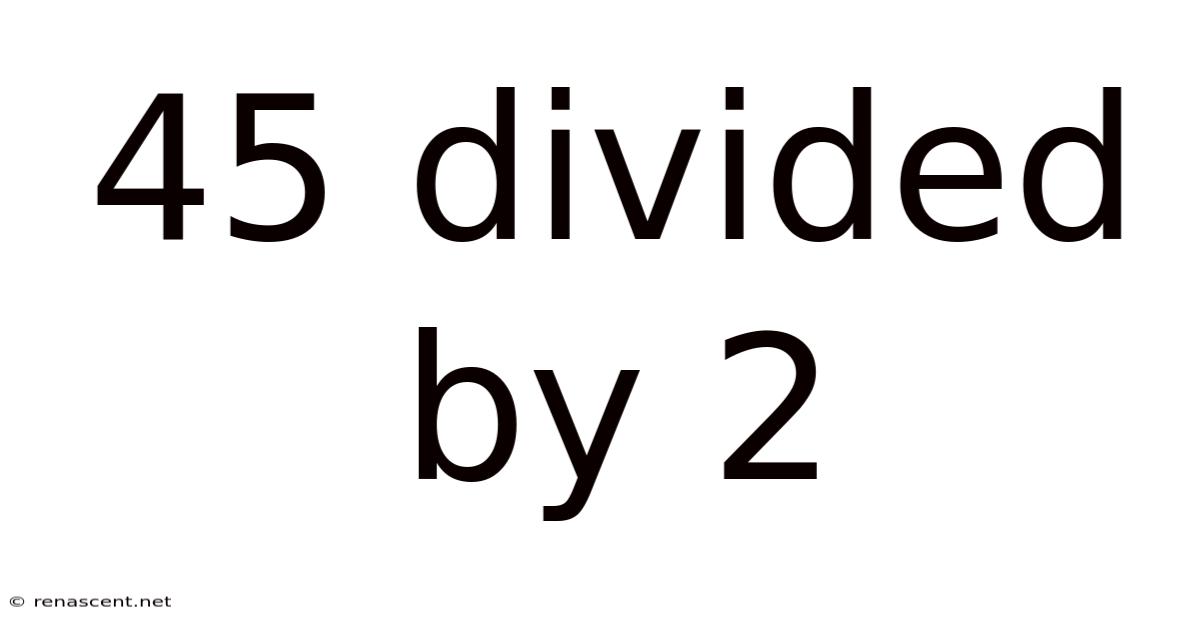
Table of Contents
45 Divided by 2: A Deep Dive into Division and its Applications
This article explores the seemingly simple calculation of 45 divided by 2, delving far beyond the basic answer to uncover the underlying mathematical concepts and practical applications. We'll unpack different methods of solving this problem, discuss the significance of remainders, and examine how this type of division problem appears in various real-world scenarios. Understanding this seemingly simple calculation forms the foundation for more complex mathematical operations and problem-solving skills.
Introduction: Understanding Division
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts. In the context of "45 divided by 2," we are asking: "How many times does 2 go into 45?" or "If we split 45 into two equal groups, how many will be in each group?"
The basic notation for division is represented in several ways:
- 45 ÷ 2
- 45 / 2
- 2)45
All three notations express the same operation: dividing 45 by 2.
Calculating 45 Divided by 2: The Standard Method
The most straightforward approach involves long division. Here's how it works:
-
Set up the problem: Write 45 as the dividend (the number being divided) and 2 as the divisor (the number we're dividing by).
-
Divide the tens digit: 2 goes into 4 two times (2 x 2 = 4). Write the "2" above the "4" in 45.
-
Subtract: Subtract (4 - 4 = 0).
-
Bring down the ones digit: Bring down the "5" from 45.
-
Divide the ones digit: 2 goes into 5 two times (2 x 2 = 4). Write the "2" above the "5".
-
Subtract: Subtract (5 - 4 = 1). This is the remainder.
Therefore, 45 divided by 2 is 22 with a remainder of 1. We can write this as: 45 ÷ 2 = 22 R1. This means that 45 can be divided into two groups of 22, with one item left over.
Understanding the Remainder
The remainder (1 in this case) is a crucial part of the answer and represents the amount left over after the division process. It signifies that the dividend (45) is not perfectly divisible by the divisor (2). The remainder's significance becomes clear when considering real-world applications. For example, if you have 45 apples and want to divide them equally between two people, each person would receive 22 apples, and one apple would remain.
Alternative Methods: Fractions and Decimals
While long division provides a clear step-by-step method, we can also express the answer as a fraction or a decimal.
-
Fraction: The result can be expressed as a mixed number: 22 1/2. This indicates 22 whole units and one-half of a unit.
-
Decimal: To express the answer as a decimal, we can continue the division process beyond the remainder. After subtracting 4 from 5, we add a decimal point and a zero to the remainder (1). Then we continue dividing: 2 goes into 10 five times. This results in 22.5. This decimal representation shows that each of the two groups would receive 22.5 units.
Real-World Applications of Division with Remainders
The concept of division, particularly with remainders, appears frequently in everyday situations. Here are a few examples:
-
Sharing resources: As illustrated with the apples, dividing items among people often results in remainders, requiring a decision on how to handle the leftover items.
-
Pricing and discounts: Calculating discounts or splitting bills evenly might leave a remainder, requiring rounding up or down depending on the context.
-
Measurement and construction: When cutting materials, such as wood or fabric, into equal lengths, remainders represent leftover material.
-
Scheduling and resource allocation: Dividing tasks or work hours among a team might yield remainders that require careful consideration in scheduling.
-
Data analysis and statistics: Remainders can be significant in statistical calculations and data interpretation, highlighting patterns or outliers.
Deeper Dive: Exploring Mathematical Concepts
The simple problem of 45 ÷ 2 opens doors to exploring broader mathematical concepts:
-
Even and Odd Numbers: The remainder of 1 indicates that 45 is an odd number. Odd numbers always leave a remainder of 1 when divided by 2. Even numbers have a remainder of 0.
-
Prime Factorization: Understanding the prime factorization of 45 (3 x 3 x 5) can help visualize the division process in terms of prime factors.
-
Modular Arithmetic: The remainder (1) in 45 ÷ 2 is the result in modular arithmetic, specifically modulo 2. This concept is crucial in various fields like cryptography.
-
Euclidean Division: This theorem states that for any two integers, a (dividend) and b (divisor) where b is not zero, there exist unique integers q (quotient) and r (remainder) such that a = bq + r, and 0 ≤ r < |b|. This formally defines the relationship between the dividend, divisor, quotient, and remainder.
Frequently Asked Questions (FAQs)
Q1: What is the best way to solve 45 divided by 2?
A1: The most efficient and universally understood method is long division. However, expressing the answer as a fraction (22 1/2) or a decimal (22.5) can be equally valid, depending on the context.
Q2: Why is there a remainder?
A2: A remainder exists because 45 is not perfectly divisible by 2. It means that 45 cannot be divided into two equal whole-number groups without having something left over.
Q3: How do I handle the remainder in real-life situations?
A3: The handling of the remainder depends on the specific context. Sometimes you might round up or down, distribute the remainder unequally, or simply note the leftover quantity.
Q4: What are some other examples of division with remainders?
A4: Many everyday scenarios involve division with remainders, such as dividing candies among friends, splitting a pizza among people, or calculating the number of cars needed to transport a group of people (if the number of passengers doesn't perfectly divide by the car capacity).
Conclusion: The Significance of a Simple Calculation
The seemingly simple calculation of 45 divided by 2 provides a foundation for understanding crucial mathematical concepts and their application in diverse fields. From basic arithmetic to advanced mathematical theories, the principles illustrated by this problem are indispensable. Understanding division, including the significance of remainders, is essential for developing problem-solving skills and navigating everyday situations requiring equal distribution, resource allocation, and precise measurements. The ability to perform this seemingly simple calculation confidently is a stepping stone towards mastering more complex mathematical challenges. The remainder, often overlooked, highlights the richness and nuances of even the most fundamental arithmetic operations.
Latest Posts
Latest Posts
-
54 Divided By 12
Sep 24, 2025
-
Harmful Crossword Puzzle Clue
Sep 24, 2025
-
355 Mm To Inches
Sep 24, 2025
-
700 Divided By 2
Sep 24, 2025
-
How To Neutralize Hcl
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 45 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.