5 12 3 4
renascent
Sep 21, 2025 · 6 min read
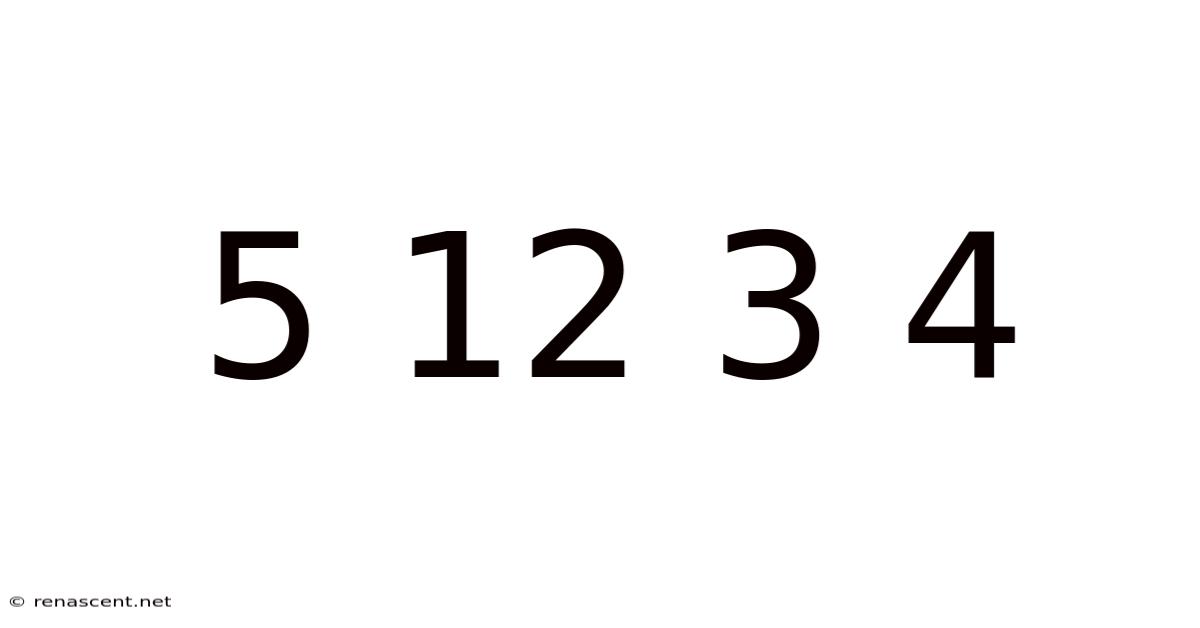
Table of Contents
Decoding the Sequence: Unveiling the Mysteries Behind 5 12 3 4
The seemingly simple sequence 5, 12, 3, 4 might appear random at first glance. However, the beauty of mathematics lies in its ability to reveal patterns and connections where initially none seem apparent. This article will delve into various approaches to understanding this sequence, exploring different mathematical concepts and demonstrating how seemingly disparate numbers can be linked through logical reasoning and creative problem-solving. We will explore potential patterns, discuss underlying mathematical principles, and consider how different interpretations can lead to diverse yet valid conclusions. This journey will not only decipher the possible meaning behind this sequence but also highlight the power of mathematical thinking and its capacity to unlock hidden order in seemingly chaotic data.
Potential Interpretations and Patterns: A Multifaceted Approach
There's no single "correct" answer when interpreting a numerical sequence without additional context. The lack of obvious mathematical operations connecting these numbers necessitates a broader approach. Let's explore several possibilities:
1. Considering Individual Number Properties:
Let's examine the individual numbers: 5, 12, 3, 4.
- 5: A prime number, also the fifth Fibonacci number (if we consider 0 and 1 as the first two).
- 12: A highly composite number (more divisors than any smaller positive integer), divisible by 2, 3, 4, and 6.
- 3: A prime number, the third Fibonacci number.
- 4: A perfect square (2²), also a highly composite number.
The presence of prime and composite numbers, as well as a Fibonacci number and a perfect square, suggests a lack of a simple, consistent arithmetic progression. However, this analysis forms the basis for further investigation. We might look for connections between the types of numbers, rather than direct arithmetic relationships.
2. Exploring Arithmetic Relationships:
While no single arithmetic operation (addition, subtraction, multiplication, division) directly links all numbers, let's look for patterns within subsets:
- Difference: The differences between consecutive numbers are: 7, -9, -1. No readily apparent pattern emerges here.
- Ratio: The ratios between consecutive numbers are: 2.4, 0.25, 4/3. Again, no clear pattern.
3. Considering Modular Arithmetic:
Modular arithmetic examines remainders after division. Let's examine the remainders when each number is divided by various integers:
- Modulo 2: 1, 0, 1, 0 - This shows an alternating pattern of odd and even numbers.
- Modulo 3: 2, 0, 0, 1 - No obvious pattern.
- Modulo 4: 1, 0, 3, 0 - No clear pattern.
- Modulo 5: 0, 2, 3, 4 - No discernible pattern.
4. Hidden Codes or Cryptography:
Could the sequence represent a hidden code or a cipher? Without further information, this is difficult to ascertain. However, it's a valid line of inquiry to consider if the sequence originates from a specific context, like a puzzle or a cryptographic message. Different types of ciphers, such as substitution ciphers or transposition ciphers, could potentially utilize this numerical sequence as a key or an element in their encoding.
5. Geometric or Spatial Representation:
Could the numbers represent points on a coordinate plane or vertices of a geometric shape? This possibility warrants exploration. However, without additional context, determining if the sequence represents specific coordinates or elements within a geometric structure requires more data or a clearer definition of the problem.
Expanding the Possibilities: Beyond Basic Arithmetic
The limitations of simple arithmetic operations necessitate exploring more advanced mathematical concepts.
1. Fibonacci-like Sequences:
Although the sequence doesn't directly follow the Fibonacci sequence (where each number is the sum of the two preceding numbers), it's plausible that a modified or generalized Fibonacci-like sequence might be involved. Exploring variations in the recursive relationship defining the sequence (e.g., adding different weights to previous terms, introducing other operations) could reveal underlying patterns.
2. Prime Number Distribution:
The inclusion of prime numbers (3 and 5) raises the possibility of a pattern related to the distribution of prime numbers. Exploring the gaps between prime numbers, prime factorization, or other prime-related properties might provide clues. The appearance of 12, a highly composite number, introduces an interesting counterpoint, potentially suggesting a relationship between prime and composite numbers within the sequence.
3. Number Theory Concepts:
Number theory offers various tools for analyzing integer sequences. Concepts like congruences, divisors, and modular arithmetic (as explored earlier), as well as more advanced concepts like quadratic residues or elliptic curves, could help reveal deeper mathematical structures behind the sequence. However, determining which specific concept is relevant requires further analysis or additional information.
4. Application of Advanced Mathematical Models:
More complex mathematical models, such as those used in data analysis, such as regression analysis or time series analysis, might help determine if a model can be fit to the data. It is important to note that creating such models requires significantly more data points for any reliable results to be generated.
The Importance of Context: Unlocking the Enigma
The crucial element missing from this analysis is context. Without knowing the origin or intended meaning of the sequence 5, 12, 3, 4, any interpretation remains speculative. For instance:
- A puzzle: The sequence could be a clue in a larger puzzle, requiring additional information or steps to solve.
- A code: It might represent a coded message, requiring a decryption key or algorithm.
- Data points: It could be a subset of a larger dataset, needing the complete data for meaningful analysis.
- A mathematical problem: The sequence could be part of a mathematical problem, with additional constraints or conditions defining the solution.
Frequently Asked Questions (FAQ)
Q: Is there a single correct answer to this sequence?
A: Without additional context, there is no single "correct" answer. Multiple interpretations are possible, depending on the underlying assumptions and mathematical frameworks used.
Q: Can you provide a definitive formula or rule for this sequence?
A: No, a definitive formula cannot be provided without more information. The apparent lack of a simple arithmetic or geometric progression suggests a more complex underlying structure.
Q: What other mathematical concepts could be relevant?
A: Many other mathematical concepts could be relevant, depending on the context. These include concepts from graph theory, combinatorics, and even abstract algebra.
Q: Is this sequence likely to have a practical application?
A: The practical application depends entirely on the context. Without context, it's difficult to determine if the sequence has any practical significance. However, the process of analyzing the sequence enhances problem-solving skills and mathematical reasoning.
Conclusion: Embracing the Ambiguity and the Power of Exploration
The sequence 5, 12, 3, 4 presents a fascinating challenge, illustrating the need for creative thinking and the application of diverse mathematical tools. While we cannot definitively decode its meaning without more information, the exploration itself has been valuable. It has demonstrated the importance of considering multiple perspectives, exploring different mathematical concepts, and recognizing the limitations of incomplete data. The seemingly simple sequence serves as a powerful reminder of the richness and complexity of mathematics, and the importance of context in interpreting any data. The process of analyzing this sequence highlights the value of persistence, creativity, and the power of mathematical reasoning in unlocking hidden patterns and unveiling hidden meanings within seemingly random data. The journey of exploration is often more valuable than the destination itself, especially in the realm of mathematics where the quest for understanding is a continuous and rewarding endeavor.
Latest Posts
Latest Posts
-
Rope And Wood Ladder
Sep 21, 2025
-
195 Min To Hours
Sep 21, 2025
-
Yellow Undertone Skin Color
Sep 21, 2025
-
57 Inches In Feet
Sep 21, 2025
-
200 Celsius En Fahrenheit
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 5 12 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.