5/16 In A Decimal
renascent
Sep 22, 2025 · 6 min read
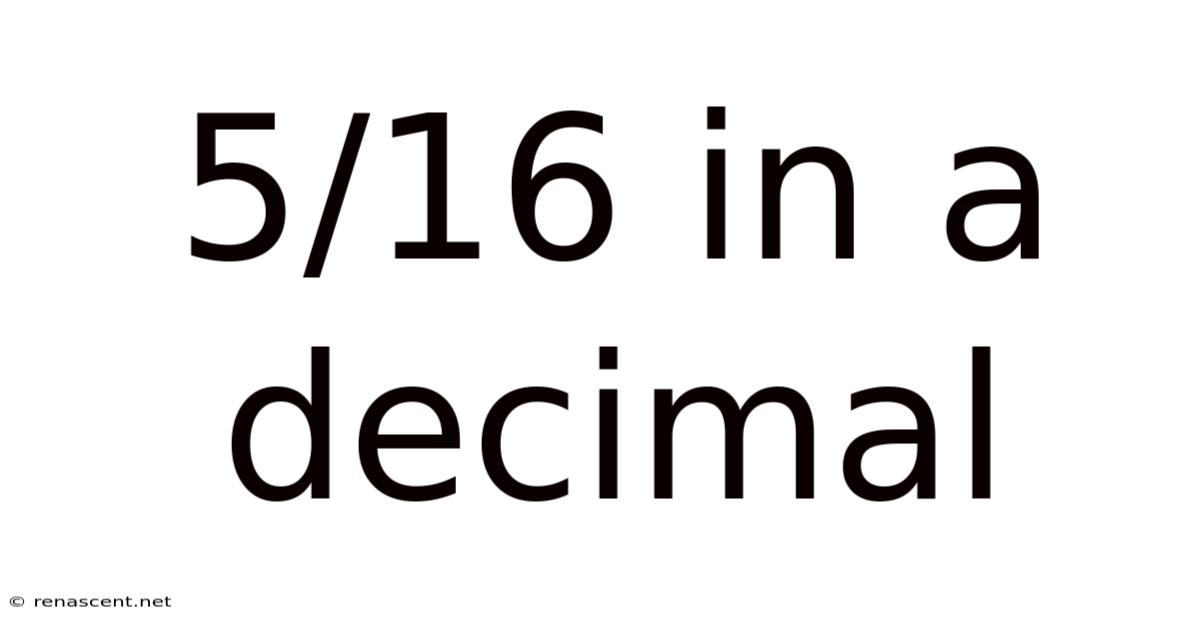
Table of Contents
Decoding 5/16: A Comprehensive Guide to Decimal Conversion and Practical Applications
Understanding fractions and their decimal equivalents is fundamental to various fields, from basic arithmetic to advanced engineering. This comprehensive guide delves into the conversion of the fraction 5/16 into its decimal form, exploring the methodology, practical applications, and addressing common questions surrounding this seemingly simple conversion. We'll move beyond the simple answer and explore the underlying principles, ensuring a complete understanding of the process and its significance.
Introduction: Why Understanding 5/16 (as a Decimal) Matters
The fraction 5/16 frequently appears in various contexts, particularly in measurements and engineering. Whether you're working on a DIY project, calculating precise dimensions, or interpreting technical specifications, knowing its decimal equivalent, 0.3125, is crucial for accurate calculations and efficient problem-solving. This article aims to provide a clear, step-by-step explanation of how to convert 5/16 to its decimal representation, along with illustrative examples and practical applications to solidify your understanding.
Method 1: Long Division - The Fundamental Approach
The most fundamental method for converting a fraction to a decimal is through long division. This method reinforces the core principles of fractions and division. Here's how to convert 5/16 using long division:
-
Set up the division: Write the numerator (5) as the dividend and the denominator (16) as the divisor.
-
Add a decimal point and zeros: Add a decimal point after the 5 and as many zeros as needed to obtain the desired level of precision. For most practical purposes, four decimal places will suffice. Therefore, you will have 5.0000 as your dividend.
-
Perform long division: Now, perform the long division as you would with any whole numbers. Remember to place the decimal point in the quotient directly above the decimal point in the dividend.
- 16 doesn't go into 5, so we put a 0 above the 5.
- 16 goes into 50 three times (16 x 3 = 48). Write down '3' above the '0' in the dividend.
- Subtract 48 from 50, leaving 2.
- Bring down the next zero, giving you 20.
- 16 goes into 20 once (16 x 1 = 16). Write down '1' above the next '0'.
- Subtract 16 from 20, leaving 4.
- Bring down the next zero, giving you 40.
- 16 goes into 40 twice (16 x 2 = 32). Write down '2' above the next '0'.
- Subtract 32 from 40, leaving 8.
- Bring down the next zero, giving you 80.
- 16 goes into 80 five times (16 x 5 = 80). Write down '5' above the final '0'.
- Subtract 80 from 80, leaving 0.
Therefore, 5 ÷ 16 = 0.3125
Method 2: Using a Calculator - A Quick and Efficient Method
While long division helps understand the underlying principle, using a calculator provides a quick and efficient way to obtain the decimal equivalent. Simply enter 5 ÷ 16 into your calculator to obtain the answer: 0.3125.
Method 3: Converting to a Decimal with Powers of 2 - An Advanced Technique
The denominator, 16, is a power of 2 (16 = 2⁴). This allows for a slightly different approach to conversion. We can express the fraction with a denominator that is a power of 10.
-
Multiply numerator and denominator: To get a denominator that is a power of 10, we need to multiply both the numerator and denominator by a number that makes the denominator a power of 10. Since 16 is 2⁴, we need to multiply by 5⁴ (625) to reach 10⁴ (10000).
-
Calculate: (5 x 625) / (16 x 625) = 3125 / 10000
-
Convert to decimal: This fraction readily converts to a decimal by moving the decimal point four places to the left: 0.3125
This method is particularly useful when dealing with fractions with denominators that are powers of 2 or 5, or combinations thereof.
Understanding the Decimal: 0.3125 Explained
The decimal 0.3125 represents 3125 ten-thousandths. This means that if we divide a whole into 10,000 equal parts, 0.3125 represents 3125 of those parts.
Practical Applications of 5/16 and its Decimal Equivalent (0.3125)
The fraction 5/16, and its decimal equivalent 0.3125, find applications in numerous fields:
-
Engineering and Manufacturing: Precise measurements are crucial in engineering and manufacturing. Dimensions are often specified using fractions, and their decimal equivalents are necessary for computer-aided design (CAD) software and machine programming. For instance, a bolt with a diameter of 5/16 inch would be 0.3125 inches in decimal form.
-
Construction: Similar to engineering, construction projects require precise measurements. Calculations involving lumber, pipes, and other materials often utilize fractions, making the conversion to decimals vital for calculations.
-
Machining: In machining processes, precise measurements are paramount for creating parts that fit together perfectly. The ability to convert fractions like 5/16 to decimals ensures that the machines can operate with the correct dimensions.
-
Cooking and Baking: While less precise than engineering, baking and cooking often involve measurements using fractions. Understanding decimal equivalents can help adjust recipes or scale them up or down accurately.
-
Finance: While less common, decimal conversions can be useful in finance for calculations involving interest rates or proportions.
-
Data Analysis: Fractional data might need to be converted into decimals for easier manipulation and analysis in statistical software.
Frequently Asked Questions (FAQs)
Q1: Is 0.3125 the only decimal representation of 5/16?
A1: Yes, 0.3125 is the exact decimal representation of 5/16. There are no other exact decimal representations. Any other values would be approximations.
Q2: How can I convert other fractions to decimals?
A2: You can use any of the methods described above: long division, a calculator, or, if the denominator is a power of 2 or 5 (or a combination), you can manipulate the fraction to obtain a denominator that's a power of 10.
Q3: What if I need more decimal places?
A3: If higher precision is needed, simply add more zeros to the dividend during long division or use a calculator with a higher level of decimal precision. However, for most practical applications, four decimal places (0.3125) provide sufficient accuracy.
Q4: Why is understanding decimal equivalents important?
A4: Understanding decimal equivalents of fractions is essential for seamless integration between different measurement systems (fractions and decimals) and for calculations involving both systems. It is particularly crucial in fields where precision is paramount, such as engineering and manufacturing.
Q5: Are there any online tools to help with fraction-to-decimal conversion?
A5: While we are not linking to external websites, you can easily find many online tools through a simple web search for "fraction to decimal converter." These tools can quickly convert fractions to decimals, providing another convenient method for this type of conversion.
Conclusion: Mastering the Conversion and its Significance
Converting 5/16 to its decimal equivalent, 0.3125, might seem like a simple task, but understanding the underlying principles and the diverse applications of this conversion is crucial for various fields. Whether you are a student learning basic arithmetic, an engineer working on a complex project, or a DIY enthusiast tackling a home improvement task, mastering this conversion will enhance your problem-solving skills and ensure accuracy in your calculations. The methods presented here—long division, calculator use, and the power-of-2 method—provide versatile approaches to tackling fraction-to-decimal conversions, empowering you with the knowledge and skills to handle similar conversions with confidence. Remember, the key is understanding the process, not just memorizing the answer.
Latest Posts
Latest Posts
-
153 Kilograms To Pounds
Sep 22, 2025
-
102 Inches To Mm
Sep 22, 2025
-
Acetic Anhydride Molar Mass
Sep 22, 2025
-
All Sorts Indoor Sports
Sep 22, 2025
-
Brake Booster Adjustment Rod
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 5/16 In A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.