5 3 X 7
renascent
Sep 19, 2025 · 6 min read
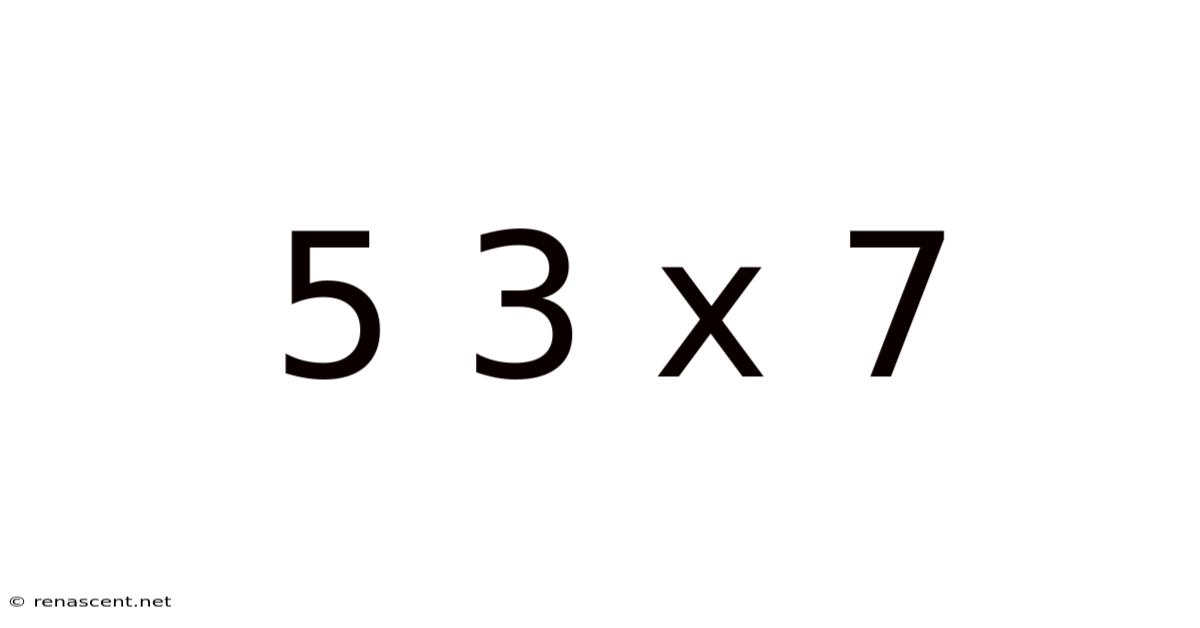
Table of Contents
Decoding 5 x 3 x 7: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple mathematical expression "5 x 3 x 7," delving far beyond the basic answer. We'll unpack the fundamental concepts of multiplication, examine different approaches to solving this problem, and explore its relevance in various real-world scenarios. Understanding this seemingly simple equation provides a solid foundation for grasping more complex mathematical concepts. Whether you're a student brushing up on your multiplication skills or someone curious about the broader implications of this equation, this guide will provide valuable insights.
Introduction to Multiplication
Multiplication is a fundamental arithmetic operation representing repeated addition. Instead of adding the same number multiple times (e.g., 5 + 5 + 5), we can use multiplication to express this more concisely (e.g., 5 x 3). In our example, "5 x 3 x 7" involves three numbers: 5, 3, and 7. This indicates we're performing repeated additions across multiple stages. We could interpret this as:
- Adding five, three times, and then multiplying the result by seven.
- Adding three, five times, and then multiplying the result by seven.
- Adding seven, fifteen times.
Solving 5 x 3 x 7: Different Approaches
There are several ways to solve 5 x 3 x 7, each demonstrating different aspects of multiplication:
1. Sequential Multiplication: This involves solving the equation step-by-step, from left to right.
- First, multiply 5 x 3 = 15
- Then, multiply the result by 7: 15 x 7 = 105
2. Commutative Property: The commutative property of multiplication states that the order of the numbers doesn't affect the final product. This means we can rearrange the numbers in any order and still get the same answer. Let's explore some possibilities:
- 3 x 5 x 7 = 105
- 7 x 3 x 5 = 105
- 7 x 5 x 3 = 105
This property significantly simplifies calculations, allowing us to choose the order that's easiest to compute. For example, multiplying 3 x 7 (21) first, then multiplying by 5 (105) might be easier for some than the sequential method.
3. Distributive Property: The distributive property allows us to break down a multiplication problem into smaller, more manageable parts. While less efficient for this specific problem, it's vital for understanding more complex equations. Let's illustrate:
Let's say we rewrite the equation as (5 x 3) x 7. We can distribute the 7:
- 7 x 5 x 3 = (7 x 5) x 3 + (7 x 0) x 3 = 35 x 3 = 105
This approach becomes more beneficial when dealing with equations involving addition or subtraction within parentheses.
4. Mental Math Techniques: With practice, you can develop mental math techniques to solve such problems quickly. For instance, recognizing that 5 x 7 = 35 simplifies the calculation considerably. Then, multiplying 35 by 3 is relatively straightforward. This emphasizes the importance of memorizing multiplication tables.
The Significance of Multiplication in Various Fields
The seemingly simple calculation of 5 x 3 x 7 extends far beyond basic arithmetic. It underpins numerous concepts and applications across various fields:
1. Everyday Calculations: We encounter multiplication daily. Shopping (calculating the total cost of multiple items), cooking (scaling recipes), calculating distances, budgeting, and many other routine activities require multiplication skills.
2. Geometry and Measurement: Calculating area and volume depends on multiplication. For example, finding the volume of a rectangular prism requires multiplying its length, width, and height.
3. Algebra and Advanced Mathematics: Multiplication forms the foundation of algebraic expressions, equations, and more complex mathematical concepts such as calculus and linear algebra.
4. Computer Science: Multiplication is fundamental to computer programming, particularly in areas like graphics processing, data analysis, and algorithm design.
5. Physics and Engineering: Many physical phenomena and engineering calculations rely heavily on multiplication, including force calculations, energy calculations, and circuit analysis.
6. Finance and Economics: Interest calculations, investment growth, and economic modeling often employ multiplication to represent growth, decay, or relationships between different variables.
7. Data Analysis and Statistics: Multiplication plays a crucial role in calculating averages, probabilities, and correlations within datasets.
5 x 3 x 7 in Real-World Scenarios
Let's apply our understanding of 5 x 3 x 7 to concrete scenarios:
Scenario 1: Organizing Books: Imagine you have 5 shelves, each holding 3 rows of books, with 7 books in each row. The total number of books is 5 x 3 x 7 = 105.
Scenario 2: Baking Cookies: Suppose a cookie recipe calls for 3 batches, each using 5 cups of flour and 7 eggs per batch. Calculating the total amount of flour and eggs needed involves multiplication: Flour: 5 x 3 = 15 cups, Eggs: 7 x 3 = 21 eggs. While this doesn’t directly use all three numbers together in a single calculation, the concept of multiplication is fundamental to scaling the recipe.
Scenario 3: Calculating Earnings: If you earn $7 per hour, work 5 days a week, and work 3 hours per day, your weekly earnings would be 7 x 5 x 3 = $105.
Scenario 4: Packaging Products: A company produces boxes holding 7 items each. They arrange 5 boxes across and 3 boxes down. The total number of items in the arrangement is 5 x 3 x 7 = 105.
Advanced Concepts: Exploring Beyond the Basics
While 5 x 3 x 7 represents a straightforward multiplication problem, understanding its underlying principles opens doors to more complex mathematical concepts:
- Exponents: Repeated multiplication can be expressed using exponents (e.g., 5³ = 5 x 5 x 5). Though not directly applicable here, the concept is closely related.
- Factorials: The factorial of a number (denoted by !) represents the product of all positive integers up to that number. While not directly involved in 5 x 3 x 7, it demonstrates the broader context of multiplication in combinatorics and probability.
- Matrices: In linear algebra, matrices are rectangular arrays of numbers, and matrix multiplication involves applying specific rules to combine matrices. The fundamental operation of element-wise multiplication is foundational to matrix operations.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to solve 5 x 3 x 7?
A: The easiest way is often subjective and depends on individual preferences and mathematical fluency. However, rearranging the numbers using the commutative property to prioritize easier calculations (e.g., 3 x 7 = 21, then 21 x 5 = 105) is often efficient.
Q: Why is the order of numbers in multiplication not important?
A: This is due to the commutative property of multiplication. The order in which you multiply numbers does not change the result.
Q: What if I have more than three numbers to multiply?
A: You can extend the same principles to multiply any number of factors. Simply multiply two numbers at a time, proceeding sequentially or using the commutative property to optimize the calculation.
Q: How does understanding 5 x 3 x 7 help me in real life?
A: Mastering this basic multiplication helps in numerous daily tasks, from shopping and cooking to understanding more complex concepts in various fields, including finance, engineering, and computer science.
Conclusion: The Power of Simple Arithmetic
This in-depth exploration of "5 x 3 x 7" demonstrates that even seemingly simple mathematical expressions hold immense value. Understanding the underlying principles of multiplication – including the commutative and distributive properties – is crucial for building a strong foundation in mathematics and applying these skills to real-world problems. The ability to perform accurate and efficient calculations is an invaluable skill that extends beyond the classroom and into all aspects of life. While the answer to 5 x 3 x 7 is simply 105, the journey of understanding its implications provides a wealth of knowledge and reinforces the power of fundamental mathematical concepts.
Latest Posts
Latest Posts
-
Diesel Engine Firing Order
Sep 19, 2025
-
164 Pounds In Kg
Sep 19, 2025
-
145 Mins In Hours
Sep 19, 2025
-
Example Of An Srs
Sep 19, 2025
-
1 5 To A Percent
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 5 3 X 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.