5 4 X 2
renascent
Sep 15, 2025 · 5 min read
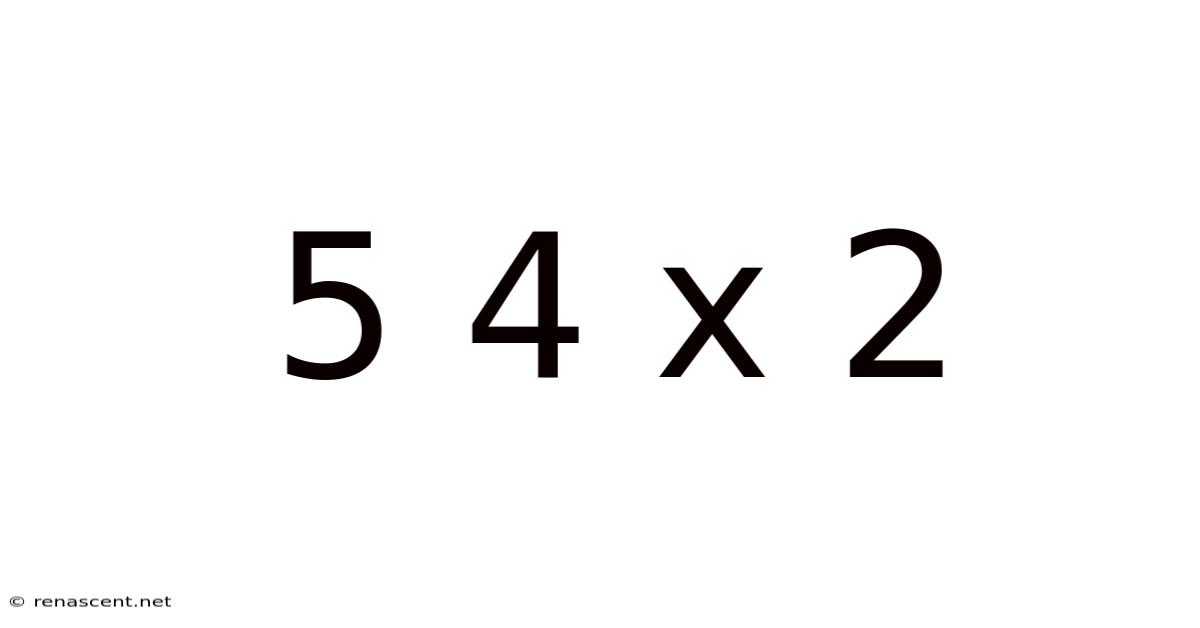
Table of Contents
Decoding 5 4 x 2: A Deep Dive into Mathematical Operations and Their Applications
This article explores the seemingly simple mathematical expression "5 4 x 2," delving beyond the immediate calculation to uncover the underlying principles of order of operations, the importance of mathematical notation, and the broader applications of these concepts in various fields. We'll examine different interpretations, potential ambiguities, and the crucial role of parentheses in ensuring clarity and accuracy. This exploration will be beneficial for students strengthening their foundational math skills, and for anyone interested in a deeper understanding of mathematical logic and its practical implications.
Understanding Order of Operations (PEMDAS/BODMAS)
The expression "5 4 x 2" highlights the critical importance of understanding the order of operations. Different parts of the world may use slightly different mnemonics, but the core principle remains the same. PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) and BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) both represent the same hierarchical structure. This order dictates which operation should be performed first. Without adhering to this order, we can arrive at drastically different results.
In our expression, the absence of parentheses or exponents means we prioritize multiplication before addition. Therefore, the correct interpretation and calculation proceed as follows:
- Multiplication: 4 x 2 = 8
- Addition: 5 + 8 = 13
Therefore, the solution to "5 4 x 2" is 13.
The Importance of Precise Mathematical Notation
The ambiguity that can arise from expressions like "5 4 x 2" underscores the critical need for precise mathematical notation. The lack of clear separation between the numbers and the operator can lead to misinterpretations. In more complex mathematical expressions, this lack of clarity can be catastrophic.
Consider the difference between:
- 5 + 4 x 2 (which we've already solved as 13)
- (5 + 4) x 2 = 18
- 5 + (4 x 2) = 13
These subtle differences in notation drastically alter the outcome. The use of parentheses, brackets, or other grouping symbols is essential for clarifying the intended order of operations and eliminating any potential ambiguity. This principle is crucial not only in basic arithmetic but also in advanced algebra, calculus, and beyond.
Expanding the Scope: Real-World Applications
While "5 4 x 2" might seem trivial, the underlying principles of order of operations and precise notation have vast practical applications across numerous fields:
-
Computer Programming: Programming languages strictly adhere to order of operations. Understanding this is fundamental for writing correct and efficient code. A misplaced operator can lead to program errors or incorrect calculations.
-
Engineering and Physics: Engineering calculations, particularly in structural analysis, physics, and electronics, rely heavily on precise mathematical computations. Errors in order of operations can have significant consequences, ranging from inaccurate predictions to potentially catastrophic failures in design.
-
Finance and Accounting: Accurate financial calculations are paramount. From calculating compound interest to balancing budgets, understanding order of operations is essential for avoiding errors in financial statements and forecasting.
-
Data Analysis and Statistics: In statistical analysis, performing calculations in the correct order is essential for deriving accurate results and making valid interpretations from data. Errors here can lead to flawed conclusions and potentially incorrect decision-making.
-
Everyday Life: Even in everyday situations, we encounter instances where the order of operations implicitly plays a role. For instance, when calculating the total cost of groceries, we might add the prices of individual items before applying a discount, reflecting a particular order of operations.
Beyond Basic Arithmetic: Exploring More Complex Scenarios
The simplicity of "5 4 x 2" provides a springboard to explore more complex mathematical expressions involving various operators and functions. Let’s consider some more sophisticated examples:
-
Incorporating Exponents: 5 + 4² x 2. Here, exponents take precedence, resulting in 5 + 16 x 2 = 37.
-
Including Parentheses and Multiple Operations: (5 + 4) x (2 + 3) ÷ 5. This highlights the importance of solving what’s in the parentheses first, then carrying out multiplication and division from left to right, followed by addition and subtraction. This example would solve as follows: (9) x (5) ÷ 5 = 9.
-
Introducing Functions: sin(45°) + 2 x 3. In this case, the trigonometric function sin(45°) needs to be evaluated first.
-
Variables and Algebra: 2x + 3y - 4z. Here, variables represent unknown values, and the order of operations remains crucial when substituting numerical values.
Each of these examples demonstrates the versatility and wide-ranging importance of correctly applying order of operations. The consistent application of PEMDAS/BODMAS ensures accurate results in diverse mathematical contexts.
Frequently Asked Questions (FAQ)
Q1: What if I perform the addition before the multiplication in "5 4 x 2"?
A1: If you perform the addition first (5 + 4 = 9) and then multiply by 2 (9 x 2 = 18), you arrive at an incorrect answer. This is because you've violated the order of operations, prioritizing addition over multiplication.
Q2: Are there any exceptions to PEMDAS/BODMAS?
A2: While PEMDAS/BODMAS provides a general guideline, the order of multiplication and division (and similarly, addition and subtraction) is determined from left to right. It's not that multiplication always comes before division. For instance, 12 ÷ 3 x 2 would be solved as (12 ÷ 3) x 2 = 8, not 12 ÷ (3 x 2) = 2.
Q3: Why is precise mathematical notation so important?
A3: Precise notation eliminates ambiguity, prevents errors, and ensures that everyone understands and interprets a mathematical expression in the same way. This is particularly crucial in collaborative settings or when sharing calculations with others.
Q4: How can I improve my understanding of order of operations?
A4: Practice is key. Work through numerous examples involving different combinations of operators and parentheses. Start with simple expressions and gradually increase complexity. You can also find many online resources and practice exercises to hone your skills.
Conclusion
The seemingly simple expression "5 4 x 2" serves as a powerful illustration of the fundamental importance of order of operations in mathematics. The correct application of PEMDAS/BODMAS, coupled with precise notation, is essential for accurate calculations across a wide range of disciplines. Understanding these concepts is not just about arriving at the right numerical answer; it's about grasping the underlying logical structure that governs mathematical computation and its pervasive impact on various fields, from everyday life to advanced scientific applications. Mastering this fundamental concept forms the cornerstone of further mathematical exploration and application. The seemingly simple 13 is much more than just a number – it’s a testament to the power of mathematical precision and the elegance of its underlying principles.
Latest Posts
Related Post
Thank you for visiting our website which covers about 5 4 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.