5 6 X 4
renascent
Sep 19, 2025 · 5 min read
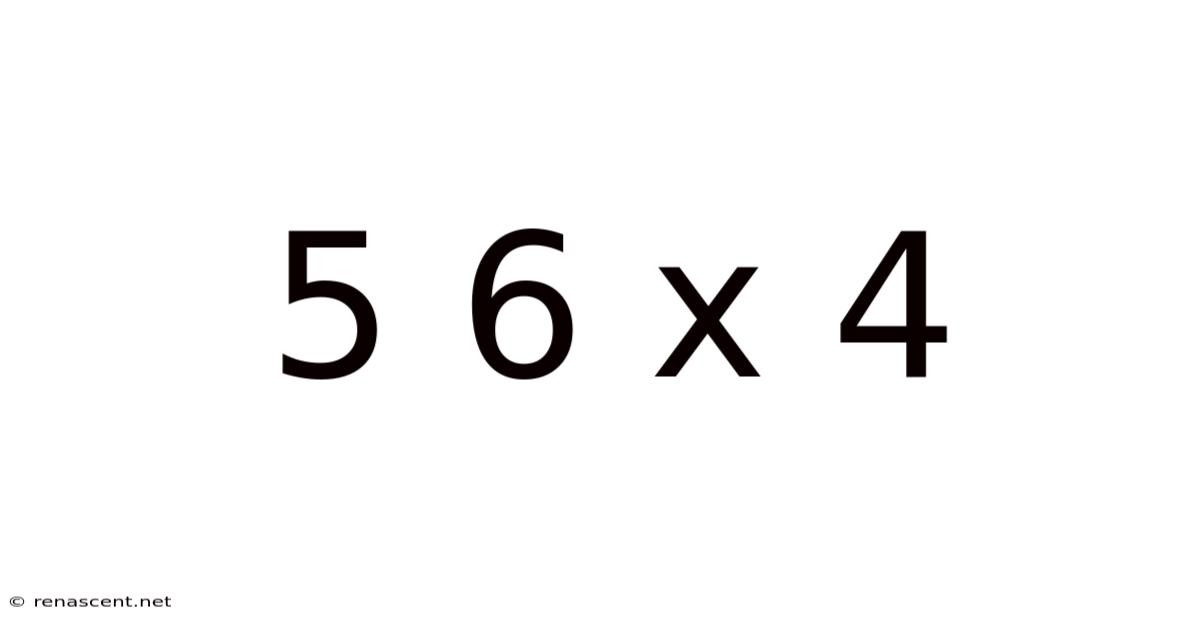
Table of Contents
Decoding 5, 6, x, and 4: Exploring Mathematical Concepts and Problem-Solving Strategies
This article delves into the seemingly simple expression "5 6 x 4," exploring the underlying mathematical concepts and demonstrating various problem-solving strategies. While the expression itself appears straightforward, its ambiguity highlights the crucial importance of order of operations and the need for precise mathematical notation. We will examine different interpretations, discuss the correct solution based on standard mathematical conventions, and explore related mathematical concepts to enhance understanding. This exploration will benefit students of mathematics at various levels, from elementary school to high school, providing a solid foundation for more complex algebraic manipulations.
Understanding the Ambiguity: Order of Operations
The core challenge with "5 6 x 4" lies in its lack of explicit operators. Without parentheses or clear indication of precedence, multiple interpretations are possible. This ambiguity underscores the critical importance of order of operations, often remembered by the acronym PEMDAS/BODMAS (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction). This established convention dictates the sequence in which mathematical operations should be performed.
Let's examine potential misinterpretations:
-
Interpretation 1: (5 + 6) x 4: This interpretation prioritizes addition before multiplication. Following this approach, we would calculate 5 + 6 = 11, and then multiply the result by 4, yielding 44.
-
Interpretation 2: 5 + (6 x 4): Here, multiplication takes precedence over addition. We compute 6 x 4 = 24, and then add 5 to obtain 29.
-
Interpretation 3: 56 x 4: This interpretation, while less likely if the numbers are written separately, assumes the expression represents a two-digit number multiplied by 4. This would result in 224.
The ambiguity highlights why clear mathematical notation is paramount. The lack of explicit operators leaves room for misinterpretations and leads to different numerical answers.
The Correct Interpretation and Solution Based on PEMDAS/BODMAS
According to the universally accepted order of operations (PEMDAS/BODMAS), multiplication takes precedence over addition. Therefore, the correct interpretation of "5 6 x 4" should be understood as 5 + (6 x 4).
Following this order:
-
Multiplication: First, we perform the multiplication: 6 x 4 = 24.
-
Addition: Next, we add 5 to the result: 5 + 24 = 29.
Therefore, the correct solution to the expression "5 6 x 4," adhering to standard mathematical conventions, is 29.
Beyond the Calculation: Exploring Related Mathematical Concepts
While solving "5 6 x 4" provides a basic understanding of order of operations, we can expand our exploration to encompass several related mathematical concepts:
1. Algebraic Expressions and Variables
The expression "5 6 x 4" can be represented algebraically. Introducing variables, we can rewrite it in different ways. For instance:
- Let 'a' = 5, 'b' = 6, and 'c' = 4. The expression becomes: a + (b x c).
This algebraic representation facilitates a more generalized approach. Instead of specific numbers, we use variables that can represent any numerical value, making the expression applicable to a wider range of problems.
2. Distributive Property
The distributive property of multiplication over addition states that a(b + c) = ab + ac. While not directly applicable to the original expression in its simplest form, we can illustrate its use with a modified example. If we had the expression 4 x (5 + 6), we could use the distributive property:
4 x (5 + 6) = (4 x 5) + (4 x 6) = 20 + 24 = 44
This demonstrates the relationship between multiplication and addition.
3. Number Systems and Operations
The numbers used in the expression (5, 6, and 4) belong to the set of natural numbers. We can extend this to include integers, rational numbers, and real numbers. The operations of addition and multiplication are fundamental to all these number systems, making the concept universally applicable.
4. Mathematical Notation and Clarity
The ambiguity of "5 6 x 4" emphasizes the critical role of precise mathematical notation. Using parentheses, brackets, and other symbols ensures clarity and prevents misinterpretations. This is particularly important in complex equations and formulas where multiple operations are involved.
Frequently Asked Questions (FAQs)
Q1: Why is the order of operations important?
A1: The order of operations ensures consistency and prevents ambiguity in mathematical calculations. Without a standard order, the same expression could yield different results depending on individual interpretation, leading to errors and inconsistencies.
Q2: What if the expression was written differently, like "5 + 6 x 4"?
A2: If the expression was explicitly written as "5 + 6 x 4," the order of operations would still apply. Multiplication would be performed before addition: 6 x 4 = 24, then 5 + 24 = 29. The answer would remain the same.
Q3: Are there any exceptions to the order of operations?
A3: While PEMDAS/BODMAS is the standard convention, parentheses or brackets can override the default order. Operations within parentheses are always performed first. This allows for flexible control over the order of calculations.
Q4: How can I improve my understanding of order of operations?
A4: Practice is key! Work through various examples, starting with simple expressions and gradually increasing complexity. Use online resources, textbooks, and interactive exercises to reinforce your understanding and build confidence.
Conclusion: The Power of Precise Mathematical Language
The seemingly simple expression "5 6 x 4" serves as a potent reminder of the significance of order of operations and the necessity of clear mathematical notation. While the correct answer, following PEMDAS/BODMAS, is 29, the ambiguity of the original expression highlights the potential for misinterpretations. Beyond the calculation itself, this exercise offers valuable insights into broader mathematical concepts, including algebraic expressions, the distributive property, number systems, and the importance of precise mathematical language. A strong understanding of these fundamental principles is crucial for success in more advanced mathematical studies and problem-solving across various fields. Remember, mathematical clarity is not merely a stylistic choice; it’s the cornerstone of accurate and reliable results.
Latest Posts
Latest Posts
-
Emission Spectra Of Neon
Sep 19, 2025
-
1 50 As Decimal
Sep 19, 2025
-
The Evil Of Banality
Sep 19, 2025
-
34 As A Decimal
Sep 19, 2025
-
25 C In K
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 5 6 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.