5 Divided By 23
renascent
Sep 19, 2025 · 5 min read
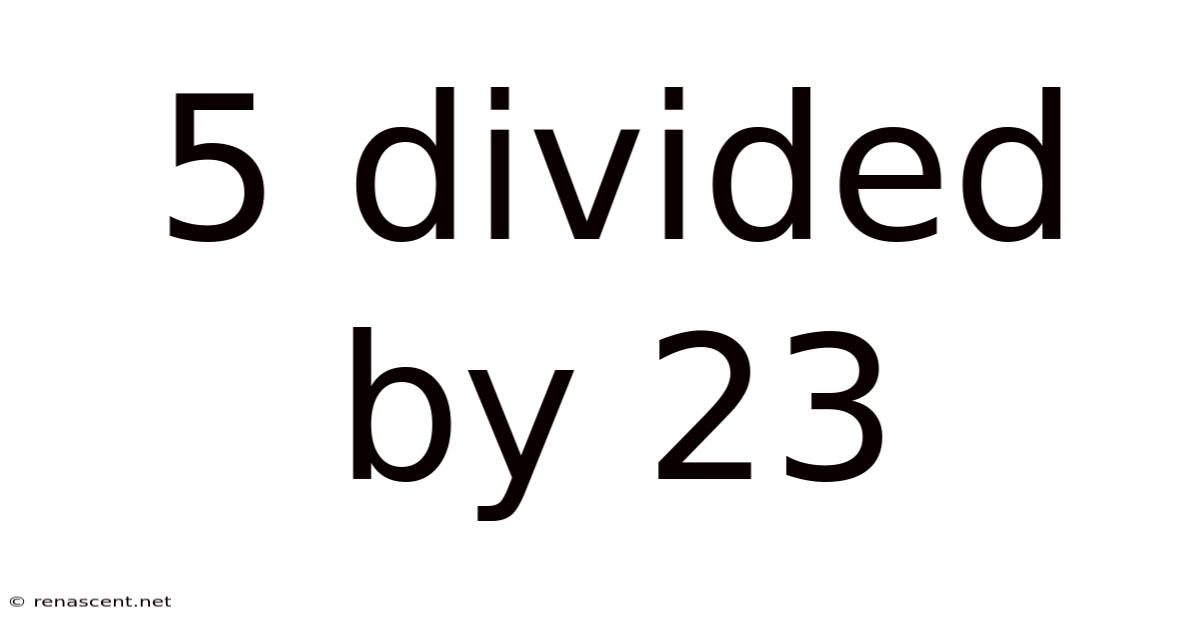
Table of Contents
Unveiling the Mystery: A Deep Dive into 5 Divided by 23
The seemingly simple question, "What is 5 divided by 23?", opens a door to a fascinating world of mathematics, encompassing division, decimals, fractions, and even the broader concepts of number systems and their applications. This article will not only provide the answer but also explore the various ways to understand and represent this division, delving into the underlying principles and demonstrating the practical implications of such calculations. We'll even touch upon the historical context of division and its ongoing relevance in the modern world.
Understanding Division: A Foundational Concept
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts. In the case of 5 divided by 23 (written as 5 ÷ 23, 5/23, or 5²) we are asking: "How many times does 23 fit into 5?" The answer, intuitively, is less than one time, as 23 is significantly larger than 5. This leads us to explore different methods of expressing this result.
Methods of Representing 5 Divided by 23
-
Fraction: The most straightforward representation is a fraction: 5/23. This fraction is already in its simplest form, meaning there are no common factors between the numerator (5) and the denominator (23). This irreducible fraction accurately represents the result of the division.
-
Decimal: To express the answer as a decimal, we perform long division. The process involves dividing 5 by 23, adding zeros after the decimal point as needed. The result is a recurring decimal: approximately 0.2173913043478260869565... The digits repeat infinitely, indicating that the decimal representation is non-terminating. This is typical when dividing by numbers that are not factors of powers of 10 (10, 100, 1000, etc.).
-
Percentage: To express the result as a percentage, we multiply the decimal value by 100. This gives us approximately 21.74%. This represents 5 as a proportion of 23.
Long Division: A Step-by-Step Approach
Let's illustrate the long division process for 5 ÷ 23:
-
Setup: Set up the long division problem with 5 as the dividend (the number being divided) and 23 as the divisor (the number dividing the dividend).
-
Decimal Point: Place a decimal point after the 5 and add zeros as needed.
-
Initial Division: Since 23 is larger than 5, we add a zero after the decimal point and perform the division of 50 by 23. 23 goes into 50 twice (2 x 23 = 46), so we write a '2' above the 0.
-
Subtraction and Bring Down: Subtract 46 from 50, resulting in 4. Bring down the next zero.
-
Continue the Process: Now we divide 40 by 23. 23 goes into 40 once (1 x 23 = 23), so we write a '1' above the next zero. Subtract 23 from 40, resulting in 17. Continue this process of bringing down zeros and dividing.
-
Recurring Decimal: You will observe that the remainder will never reach zero, and the digits in the quotient (the answer) will begin to repeat. This signifies a recurring or repeating decimal.
Practical Applications of 5/23
While the division of 5 by 23 might seem abstract, it has numerous practical applications in various fields:
-
Proportions and Ratios: The fraction 5/23 represents a specific ratio or proportion. This type of calculation is crucial in fields like chemistry (mixing solutions), engineering (scaling models), and finance (calculating percentages).
-
Probability: Imagine a scenario where there are 23 equally likely outcomes, and 5 of them represent a successful event. The probability of this successful event is precisely 5/23, which can then be converted to a decimal or percentage for easier interpretation.
-
Data Analysis and Statistics: Calculating proportions and percentages is fundamental to statistical analysis. Understanding how to express and interpret values like 5/23 allows for accurate representation and interpretation of data.
-
Computer Programming: Computers frequently deal with fractional numbers and often require accurate representation of recurring decimals. Understanding the nature of this division is essential for programmers working with precision-sensitive applications.
Exploring Number Systems: Beyond Decimal
While we've focused on the decimal representation, it's worth considering other number systems. In binary (base-2), the representation of 5/23 would be quite different, involving binary fractions. This highlights that the specific representation of a number depends on the chosen number system.
Historical Context: The Evolution of Division
The concept of division has a rich history, evolving alongside the development of number systems and mathematical understanding. Ancient civilizations used various methods for division, from simple physical partitioning to the development of algorithmic approaches. The development of long division as we know it today is a culmination of centuries of mathematical progress.
Frequently Asked Questions (FAQ)
-
Q: Is 5/23 a rational number? A: Yes, 5/23 is a rational number because it can be expressed as a fraction of two integers.
-
Q: Can 5/23 be simplified? A: No, 5/23 is already in its simplest form because 5 and 23 share no common factors other than 1.
-
Q: How many digits repeat in the decimal representation of 5/23? A: The repeating block of digits in the decimal representation of 5/23 has 22 digits. This is related to the properties of the denominator (23) and its prime factorization.
-
Q: What is the significance of the recurring decimal in this case? A: The recurring decimal shows that the result of the division is a non-terminating decimal, meaning it continues infinitely. This is common when dividing integers that do not result in a whole number quotient.
Conclusion: A Deeper Understanding of Division
The seemingly simple calculation of 5 divided by 23 reveals a wealth of mathematical concepts and practical applications. From fractions and decimals to percentages and the broader context of number systems, this seemingly simple question allows us to explore the foundations of arithmetic and its pervasive influence in various aspects of our lives. This detailed exploration highlights the importance of understanding not just the answer, but also the underlying principles and methods involved in performing and interpreting division. It emphasizes the beauty and practical utility of seemingly simple mathematical operations. The next time you encounter a similar division problem, remember the journey taken here—from simple calculation to a deep understanding of the underlying concepts. This deeper understanding will enhance your mathematical literacy and problem-solving abilities across numerous disciplines.
Latest Posts
Latest Posts
-
500 Minutes In Hours
Sep 19, 2025
-
51 5 Kg In Pounds
Sep 19, 2025
-
175 Celsius In Fahrenheit
Sep 19, 2025
-
0 4 As A Percent
Sep 19, 2025
-
2 8 As Fraction
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 5 Divided By 23 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.