5 Divided By 55
renascent
Sep 18, 2025 · 5 min read
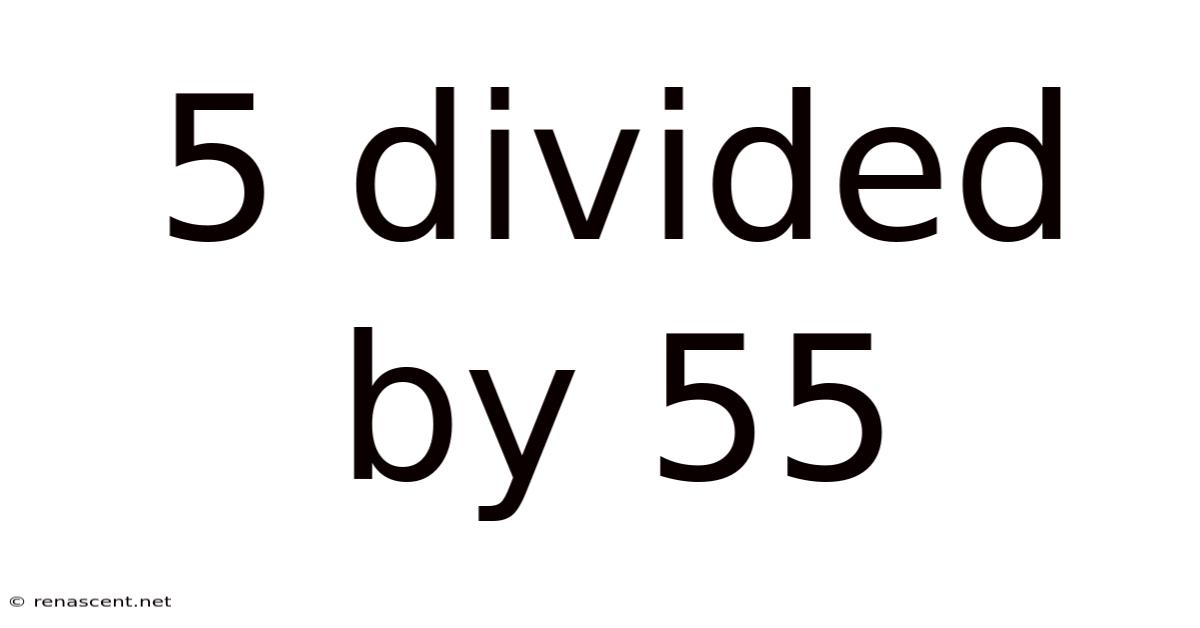
Table of Contents
Unpacking the Mystery: 5 Divided by 55
Understanding division can sometimes feel like navigating a maze, especially when dealing with numbers that don't divide evenly. This article delves into the process of dividing 5 by 55, exploring various methods and providing a comprehensive explanation that goes beyond a simple answer. We'll uncover the underlying mathematical concepts, explore different approaches to solving the problem, and address common misconceptions. Whether you're a student brushing up on your arithmetic skills or simply curious about the intricacies of division, this guide will equip you with a solid understanding. This exploration will cover long division, decimal representation, fractions, and the conceptual meaning behind the result.
Understanding Division: A Quick Refresher
Before we tackle 5 divided by 55 (often written as 5 ÷ 55 or 5/55), let's briefly revisit the fundamental concept of division. Division essentially involves splitting a quantity into equal parts. In the expression a ÷ b, 'a' is the dividend (the number being divided), and 'b' is the divisor (the number by which we're dividing). The result is called the quotient.
When the dividend is smaller than the divisor, as in our case (5 ÷ 55), the quotient will be less than 1. This often leads to confusion, but understanding this fundamental fact is crucial. We'll explore how to represent this result in different forms.
Method 1: Long Division
Long division is a traditional method for tackling division problems, especially when dealing with larger numbers or those that don't divide evenly. Let's apply this method to 5 ÷ 55:
-
Setup: Set up the long division problem like this:
55 | 5 -
Initial Observation: Since 5 is smaller than 55, we know the quotient will be less than 1. We need to add a decimal point and a zero to the dividend to continue the division process.
55 | 5.0 -
Division: 55 does not go into 5, so we put a 0 above the decimal point. Then, 55 goes into 50 zero times, so we add another zero and continue.
0. 55 | 5.00 -
Continuing the Process: Now we consider 500. How many times does 55 go into 500? We can estimate. 55 x 9 = 495. This is close to 500.
0.09 55 | 5.00 495 --- 5 -
Repeating: We bring down another zero and repeat the process. We find that 55 goes into 50 zero times. To obtain a more precise value, we could repeat the process for several more digits, but this demonstrates the pattern.
Therefore, using long division, we find that 5 ÷ 55 is approximately 0.090909...
Method 2: Converting to a Fraction
Another way to approach this problem is to represent the division as a fraction:
5 ÷ 55 = 5/55
This fraction can be simplified by finding the greatest common divisor (GCD) of 5 and 55, which is 5. Dividing both the numerator and denominator by 5, we get:
5/55 = 1/11
This simplified fraction, 1/11, is an equivalent representation of 5/55. It is a more concise way to express the result. To convert it to a decimal, you would perform the division 1 ÷ 11, which will yield the same repeating decimal: 0.090909...
Method 3: Understanding the Decimal Representation
The decimal representation of 5/55 (or 1/11) is a repeating decimal, meaning the digits 09 repeat infinitely. We can represent this using a bar notation: 0.<u>09</u>. This notation indicates that the sequence "09" repeats without end. This is a characteristic of dividing numbers where the denominator has prime factors other than 2 and 5 (in this case, 11 is a prime number).
The Significance of the Result: A Deeper Look
The result, approximately 0.09 or the fraction 1/11, represents a proportion or a ratio. It tells us that 5 is one-eleventh of 55. In other words, if you were to divide 55 into 11 equal parts, each part would be 5. This concept is crucial in various applications, from scaling recipes to calculating percentages.
Practical Applications and Real-World Examples
Understanding the concept of dividing a smaller number by a larger number is vital in many practical scenarios:
-
Proportions and Ratios: Many real-world problems involve comparing quantities. For example, if you have 5 apples and a total of 55 fruits, 5/55 (or 1/11) represents the proportion of apples to the total number of fruits.
-
Percentages: Converting a fraction or decimal into a percentage is straightforward. To find the percentage, multiply the decimal (0.0909...) by 100: 0.0909... x 100 ≈ 9.09%. This means 5 is approximately 9.09% of 55.
-
Scaling and Ratios: In cooking or construction, adjusting recipe quantities or building plans often requires dividing or multiplying fractions.
Frequently Asked Questions (FAQ)
Q1: Can I express the answer as a percentage?
A1: Yes, 1/11 or 0.0909... is approximately 9.09%.
Q2: Why does the decimal repeat?
A2: The decimal repeats because the denominator (11) contains prime factors other than 2 and 5. When the denominator only contains 2 and/or 5 as prime factors, the decimal will terminate.
Q3: Is there a simpler way to solve this problem?
A3: Simplifying the fraction 5/55 to 1/11 is the most efficient method. This simplifies the calculation and offers a clearer understanding of the relationship between the numbers.
Q4: What if I need a more precise answer?
A4: You can extend the long division process to include more decimal places to achieve a more precise approximation. However, the decimal will always repeat.
Conclusion: Mastering Division
Dividing 5 by 55, while seemingly straightforward, offers a valuable opportunity to solidify your understanding of division, fractions, decimals, and their real-world applications. Whether you choose long division, fraction simplification, or focus on the decimal representation, each method provides a unique perspective and reinforces the fundamental concepts of mathematics. Remember that the seemingly simple act of dividing numbers can lead to a deeper appreciation of mathematical relationships and their practical significance in everyday life. The key takeaway is not just the numerical answer (approximately 0.09 or 1/11), but the comprehensive understanding of the process and its applications. This problem highlights the importance of simplifying fractions and understanding repeating decimals, crucial skills in many areas of mathematics and beyond.
Latest Posts
Latest Posts
-
Colors Of The Military
Sep 18, 2025
-
1 5 To A Percentage
Sep 18, 2025
-
214 Pounds To Kg
Sep 18, 2025
-
85 Mph In Kmh
Sep 18, 2025
-
52 Degrees Centigrade Fahrenheit
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 5 Divided By 55 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.