5 X 2 6
renascent
Sep 17, 2025 · 6 min read
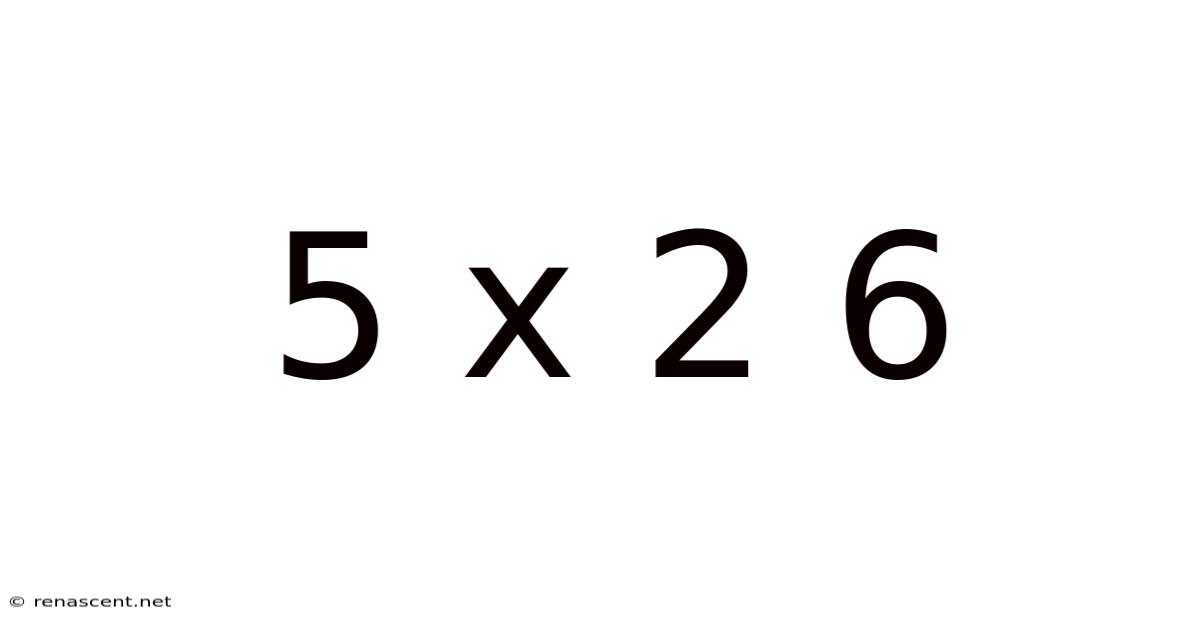
Table of Contents
Decoding 5 x 2 = 6: Exploring the World of Non-Standard Arithmetic
The seemingly simple equation "5 x 2 = 6" immediately catches the eye because it contradicts the fundamental rules of standard arithmetic. In the standard base-10 number system, 5 multiplied by 2 unequivocally equals 10. So, what does this unconventional equation represent? It opens a fascinating door to explore alternative number systems, mathematical structures, and the very nature of mathematical axioms. This article will delve into the potential interpretations of "5 x 2 = 6," examining different mathematical contexts where such a result might hold true. We'll explore modular arithmetic, alternative number bases, and even touch upon the abstract world of abstract algebra to unravel the mysteries behind this intriguing equation.
Understanding Standard Arithmetic: A Quick Recap
Before venturing into the unconventional, let's briefly review the basics of standard arithmetic. In our everyday decimal system (base-10), we represent numbers using ten digits (0-9). Multiplication is a fundamental operation that represents repeated addition. For example, 5 x 2 means adding 5 two times: 5 + 5 = 10. This is a universally accepted truth within the framework of standard base-10 arithmetic. The equation "5 x 2 = 6" directly contradicts this fundamental principle.
Modular Arithmetic: A World Beyond Remainders
One of the most plausible explanations for "5 x 2 = 6" lies in the realm of modular arithmetic. Modular arithmetic, also known as clock arithmetic, deals with remainders after division. We often encounter modular arithmetic in everyday life, like telling time. When the hour hand completes a full cycle, it resets to 12. This is equivalent to working modulo 12.
Let's explore how modular arithmetic might lead to 5 x 2 = 6. Consider a system operating modulo 4 (denoted as mod 4). In this system, numbers "wrap around" after reaching 4. Any number greater than or equal to 4 is considered equivalent to its remainder when divided by 4.
- 5 mod 4 = 1 (because 5 divided by 4 leaves a remainder of 1)
- 2 mod 4 = 2
Now, let's perform the multiplication:
(5 mod 4) x (2 mod 4) = 1 x 2 = 2
This still doesn't yield 6. However, if we were working in a different modulus, say modulo 7, we'd get:
- 10 mod 7 = 3
This is still not 6, but this example demonstrates the principle of modular arithmetic, showing how operations can lead to unexpected results depending on the chosen modulus. To get to 6, we need to explore a bit further. Let's consider a different approach within modular arithmetic.
Consider a system where we redefine multiplication. Instead of standard multiplication, let's define a new operation, denoted by ⊗, such that:
a ⊗ b = (a x b) mod m
Where 'm' is the modulus. If we want 5 ⊗ 2 = 6, and assuming we're working with integers, we can set up the equation:
(5 x 2) mod m = 6 10 mod m = 6
This implies that when 10 is divided by 'm', the remainder is 6. The solution to this is m = 4. Therefore, in a modular arithmetic system with modulus 4, using our redefined multiplication operation, 5 ⊗ 2 = 6. This highlights how a redefinition of basic operations within a specific mathematical structure can lead to seemingly contradictory results.
Alternative Number Bases: Beyond Base 10
Our usual decimal system uses base 10. However, we can represent numbers in other bases. For example, the binary system (base 2) uses only 0 and 1, while the hexadecimal system (base 16) uses digits 0-9 and letters A-F.
Could a different number base explain "5 x 2 = 6"? Let's explore this possibility. In a hypothetical base 'b', we need to find a base where the representation of 10 in base 10 is represented as 6 in this new base. This means we need to find 'b' such that:
ab<sup>1</sup> + cb<sup>0</sup> = 10 (Where 'a' and 'c' are digits in the new base)
If we assume base b is a whole number and we are representing '10' in base 10 as 6 in base 'b', it would be represented as 6<sub>b</sub>, implying that 6 = 10 in base b. This does not lead to a practical number base, but it does show that with careful selection and definition of rules for a number base, we may be able to arrive at such an equation.
However, changing the base would not only affect the representation of the numbers 5 and 2 but also the representation of the result. The equation would still not fundamentally change the multiplication operation itself.
Abstract Algebra: Exploring Group Theory
Abstract algebra provides a framework for exploring mathematical structures beyond the familiar arithmetic operations. Group theory, a branch of abstract algebra, studies algebraic structures called groups. A group is a set of elements with an operation that satisfies certain properties (closure, associativity, identity element, inverse element).
It's theoretically possible to define a group where the operation does not correspond to standard multiplication, yet the equation "5 x 2 = 6" holds true within the context of that group's operation. However, this would require defining a very specific group with its unique operation and properties, drastically different from standard arithmetic. The equation would be valid only within the constraints of this specific group structure. Such a system would require rigorous mathematical definition and would be significantly more complex to explain.
Further Exploration and Considerations:
- Fuzzy Logic: In fuzzy logic systems, where truth values are not strictly binary (true or false) but rather lie on a spectrum between 0 and 1, it's conceivable that certain operations could yield results that seem contradictory in standard Boolean logic. However, this would involve significantly altering the understanding of mathematical operations.
- Error and Approximation: The equation could represent a gross approximation or a significant rounding error within a specific context such as engineering or scientific measurement. In these cases, the equation wouldn't be mathematically accurate but may be practically acceptable given the margin of error allowed.
Conclusion: The Meaning of "5 x 2 = 6"
The equation "5 x 2 = 6" is not true within the framework of standard arithmetic. However, its very existence compels us to consider the limitations of our mathematical assumptions and the vast landscape of alternative mathematical structures. Modular arithmetic, particularly when considering redefined operations, offers a plausible and understandable explanation. Alternative number bases and abstract algebra could also theoretically lead to such an outcome but would require significantly more complex mathematical systems. The equation should be viewed as a springboard for exploring the rich and multifaceted world of mathematics beyond the conventional, encouraging critical thinking and a deeper appreciation for the underlying axioms and structures that govern different mathematical systems. The key takeaway is that mathematical truths are always context-dependent. While "5 x 2 = 10" is a cornerstone of standard arithmetic, alternative systems exist where different outcomes are possible, provided the rules of the system are clearly defined and consistently applied.
Latest Posts
Latest Posts
-
Mean Of Frequency Table
Sep 17, 2025
-
Ounces In 200 Ml
Sep 17, 2025
-
World War One Sources
Sep 17, 2025
-
Easy Doodling Mandala Art
Sep 17, 2025
-
2000 Hours Into Days
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 5 X 2 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.