50 Percent Of 40
renascent
Sep 18, 2025 · 5 min read
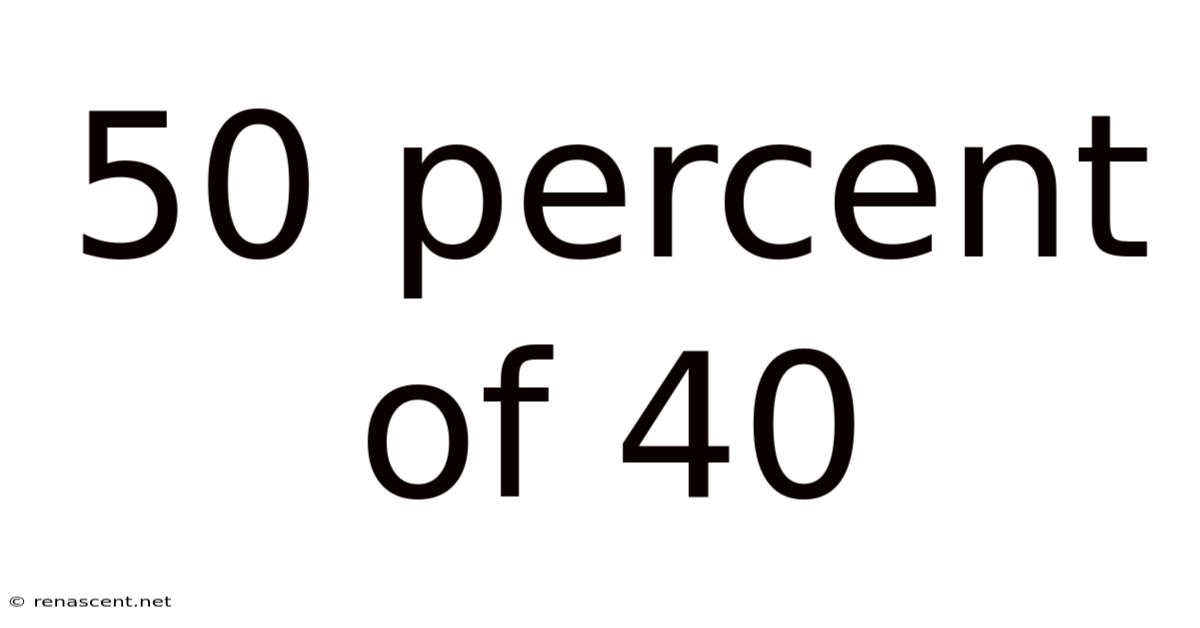
Table of Contents
Unpacking 50% of 40: A Deep Dive into Percentages and Their Applications
Finding 50% of 40 might seem like a simple calculation, a piece of cake even. But this seemingly straightforward problem offers a fantastic opportunity to explore the fundamental concept of percentages, their real-world applications, and different methods for solving percentage-related problems. This article will go beyond simply providing the answer; we'll delve into the underlying mathematics, explore various approaches, and even touch upon advanced applications. Understanding percentages is crucial for various aspects of life, from managing finances to interpreting data, making this exploration both practical and intellectually enriching.
What is a Percentage?
A percentage is simply a fraction expressed as a part of 100. The word "percent" comes from the Latin "per centum," meaning "out of a hundred." So, 50% literally means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5. This fractional representation is key to understanding how percentages work.
Calculating 50% of 40: The Straightforward Approach
The most direct way to find 50% of 40 is to utilize the fractional equivalent. Since 50% is equal to 1/2, the calculation becomes:
(1/2) * 40 = 20
Therefore, 50% of 40 is 20.
This method highlights the core principle: a percentage calculation is essentially a multiplication problem involving a fraction and a whole number.
Calculating 50% of 40: The Decimal Approach
Another common method involves converting the percentage to a decimal. To do this, we divide the percentage by 100. So, 50% becomes 50/100 = 0.5. The calculation then becomes:
0.5 * 40 = 20
This approach, while seemingly different, is fundamentally the same as the fractional method; it just uses a different representation of the same fraction.
Understanding the Concept of "Of" in Percentage Calculations
The word "of" in percentage problems signifies multiplication. When we see "50% of 40," it translates mathematically to "50% multiplied by 40." This understanding is critical for correctly interpreting and solving any percentage problem.
Exploring Different Percentages of 40
Let's extend our understanding by calculating different percentages of 40. This will solidify our understanding of the process and demonstrate its versatility.
- 25% of 40: (1/4) * 40 = 10 or 0.25 * 40 = 10
- 75% of 40: (3/4) * 40 = 30 or 0.75 * 40 = 30
- 10% of 40: (1/10) * 40 = 4 or 0.10 * 40 = 4
- 20% of 40: (1/5) * 40 = 8 or 0.20 * 40 = 8
- 100% of 40: (1/1) * 40 = 40 or 1.00 * 40 = 40
These examples showcase how easily we can adapt the methods to calculate various percentages.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in everyday life. Here are a few examples:
- Sales and Discounts: Stores often advertise discounts like "50% off!" Understanding percentages allows you to quickly determine the final price of an item after a discount.
- Taxes: Sales tax is calculated as a percentage of the purchase price. Knowing how to calculate percentages helps you determine the total cost of an item, including tax.
- Tips and Gratuities: Restaurants often encourage tips as a percentage of the bill. The ability to calculate percentages swiftly aids in determining a fair tip.
- Interest Rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts.
- Data Analysis: Percentages are used extensively to represent proportions and trends in data analysis, making it easier to understand and interpret complex information.
- Grades and Scores: Academic performance is often expressed as a percentage, allowing for easy comparison and evaluation of results.
Solving Percentage Problems: A Step-by-Step Guide
Let's outline a general approach for solving any percentage problem:
- Identify the whole: This is the total amount or value you are working with. In our example, 40 is the whole.
- Identify the percentage: This is the portion you want to find. In our case, it's 50%.
- Convert the percentage to a fraction or decimal: This simplifies the calculation.
- Multiply the whole by the fraction or decimal: This gives you the answer.
Advanced Percentage Calculations: Finding the Percentage
Sometimes, instead of finding a percentage of a number, you might need to find what percentage one number is of another. For example, what percentage is 20 of 40?
To solve this, we divide the part (20) by the whole (40) and multiply by 100:
(20/40) * 100 = 50%
This demonstrates the inverse calculation – finding the percentage representation.
Advanced Percentage Calculations: Finding the Whole
Another common scenario is finding the whole when you know a part and the percentage. For example, if 50% of a number is 20, what is the number?
To solve this, we can set up an equation:
0.5 * x = 20
Solving for x (the whole number), we get:
x = 20 / 0.5 = 40
Frequently Asked Questions (FAQ)
Q: Can I use a calculator for percentage calculations?
A: Absolutely! Calculators are very helpful, especially for more complex percentage problems. However, understanding the underlying principles is still crucial.
Q: What if the percentage is greater than 100%?
A: A percentage greater than 100% simply means that the part is larger than the whole. This often occurs when dealing with percentage increases or growth rates. For example, a 150% increase means the value has increased by 1.5 times its original value.
Q: Are there any shortcuts for common percentages like 10%, 25%, 50%, and 75%?
A: Yes, understanding the fractional equivalents of these common percentages (1/10, 1/4, 1/2, and 3/4 respectively) can significantly speed up calculations.
Q: How can I improve my understanding of percentages?
A: Practice is key! Solve various percentage problems, starting with simpler ones and gradually moving towards more complex scenarios. Use online resources, worksheets, and real-life situations to reinforce your understanding.
Conclusion
While finding 50% of 40 might seem trivial at first glance, exploring this simple calculation opens a gateway to a broader understanding of percentages and their immense practical value. From everyday transactions to complex data analysis, the ability to calculate and interpret percentages is an essential skill applicable across various fields. By understanding the underlying principles and practicing different methods, you can confidently tackle any percentage-related challenge and enhance your numerical proficiency. The seemingly simple "50% of 40" becomes a springboard to a deeper understanding of mathematics and its real-world relevance. Mastering percentages is not just about numbers; it's about mastering a critical skill that empowers you to navigate the quantitative aspects of our world more effectively.
Latest Posts
Latest Posts
-
Examples For Closed System
Sep 18, 2025
-
Jennifer Harman Book Review
Sep 18, 2025
-
2 5 Ssd Hard Drive
Sep 18, 2025
-
164 Minutes To Hours
Sep 18, 2025
-
Blue Pink And Yellow
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 50 Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.