52/60 As A Percentage
renascent
Sep 24, 2025 · 5 min read
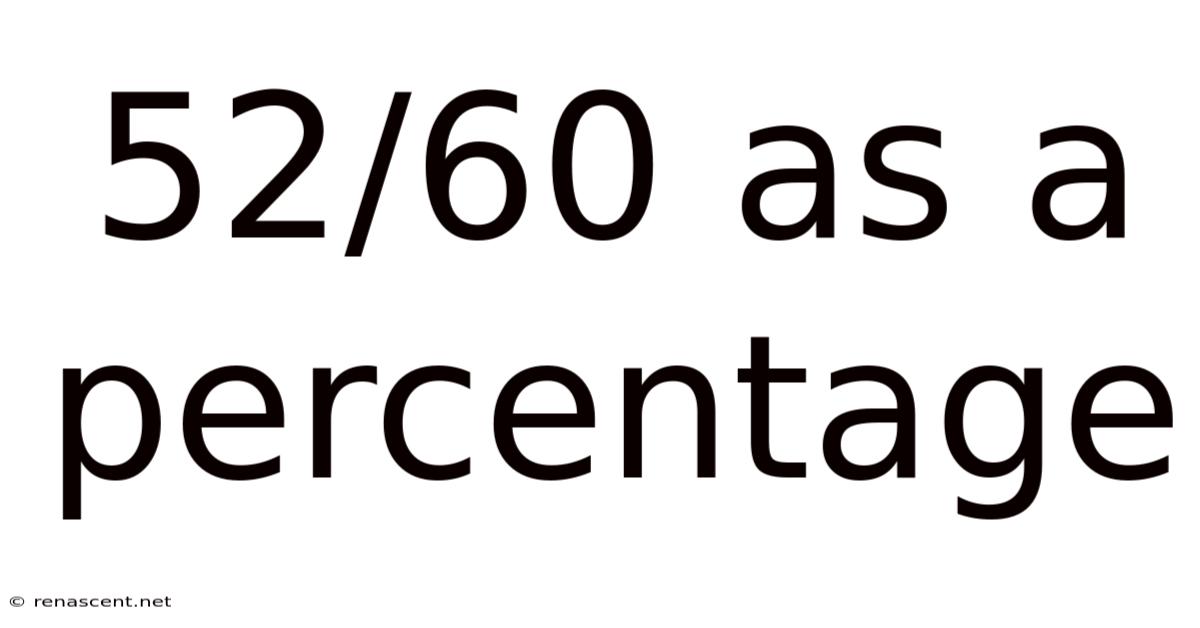
Table of Contents
Decoding 52/60 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics, applicable across numerous fields from finance and statistics to everyday life. This article delves into the conversion of the fraction 52/60 into a percentage, exploring the underlying methodology, providing step-by-step instructions, and addressing common related questions. We'll also examine the broader context of percentage calculations and their significance. This guide aims to provide a complete and easily understandable explanation for anyone wanting to master this essential mathematical concept.
Understanding Fractions and Percentages
Before we dive into the specific calculation of 52/60 as a percentage, let's briefly revisit the fundamentals. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, and the denominator indicates the total number of parts in the whole.
A percentage, on the other hand, expresses a fraction as a portion of 100. The term "percent" literally means "per hundred." Therefore, a percentage represents how many parts out of 100 a fraction represents. Converting a fraction to a percentage involves finding the equivalent fraction with a denominator of 100.
Converting 52/60 to a Percentage: Step-by-Step
The conversion of 52/60 to a percentage can be achieved using two primary methods:
Method 1: Simplifying the Fraction and then Converting
This method involves first simplifying the fraction to its lowest terms, making the conversion to a percentage easier.
-
Find the Greatest Common Divisor (GCD): The GCD of 52 and 60 is 4. This means we can divide both the numerator and denominator by 4 without changing the value of the fraction.
-
Simplify the Fraction: Dividing both the numerator and denominator by 4, we get:
52 ÷ 4 = 13 60 ÷ 4 = 15
The simplified fraction is 13/15.
-
Convert the Simplified Fraction to a Decimal: To convert a fraction to a decimal, divide the numerator by the denominator:
13 ÷ 15 ≈ 0.8667
-
Convert the Decimal to a Percentage: Multiply the decimal by 100 and add a percentage sign:
0.8667 × 100 = 86.67%
Therefore, 52/60 simplifies to 13/15, which is approximately 86.67%.
Method 2: Direct Conversion using Decimal Equivalents
This method involves directly converting the fraction to a decimal and then to a percentage.
-
Convert the Fraction to a Decimal: Divide the numerator by the denominator:
52 ÷ 60 ≈ 0.8667
-
Convert the Decimal to a Percentage: Multiply the decimal by 100 and add a percentage sign:
0.8667 × 100 = 86.67%
This method yields the same result: 86.67%.
Understanding the Result: 86.67%
The result, 86.67%, signifies that 52 represents approximately 86.67 parts out of every 100 parts when compared to the whole represented by 60. This percentage can be used in various applications, such as calculating grades, expressing proportions in data analysis, or determining discounts and increases in various contexts.
Practical Applications of Percentage Calculations
The ability to convert fractions to percentages has a wide range of practical applications:
-
Calculating Grades: If you scored 52 out of 60 on a test, your percentage score is 86.67%.
-
Financial Calculations: Percentage calculations are crucial for understanding interest rates, discounts, profit margins, and tax rates.
-
Data Analysis and Statistics: Percentages help to represent data proportions clearly and concisely in charts and graphs.
-
Everyday Life: Percentages are used extensively in everyday situations, such as calculating tips, sales tax, and discounts.
Advanced Concepts: Accuracy and Rounding
The percentage 86.67% is an approximation. The decimal representation of 13/15 is a recurring decimal (0.866666...). The level of accuracy required depends on the context. In some cases, rounding to the nearest whole number (87%) might suffice, while in others, more decimal places might be necessary for precision.
Frequently Asked Questions (FAQ)
Q1: Why is it important to simplify the fraction before converting to a percentage?
A1: Simplifying the fraction makes the division process easier and reduces the chances of errors in calculation, especially when dealing with larger numbers.
Q2: Can I use a calculator to convert fractions to percentages?
A2: Yes, most calculators have a function that allows direct conversion of fractions to percentages. Simply enter the fraction and press the appropriate button.
Q3: What if the fraction has a denominator other than 60? How does the conversion process change?
A3: The process remains the same. You always divide the numerator by the denominator to get the decimal equivalent and then multiply by 100 to obtain the percentage.
Q4: What are some common mistakes people make when converting fractions to percentages?
A4: Some common mistakes include forgetting to multiply the decimal by 100, incorrectly simplifying the fraction, and misinterpreting recurring decimals.
Q5: How can I improve my understanding of fractions and percentages?
A5: Practice is key. Work through several examples, using different fractions and denominators. Utilize online resources, educational videos, and practice worksheets to reinforce your understanding.
Conclusion
Converting 52/60 to a percentage, yielding approximately 86.67%, is a straightforward process that involves understanding the relationship between fractions, decimals, and percentages. Mastering this skill is essential for various mathematical and real-world applications. By understanding the underlying principles and employing the steps outlined in this guide, you can confidently tackle similar fraction-to-percentage conversions and enhance your mathematical proficiency. Remember that accuracy and the level of rounding are context-dependent and should be considered based on the specific application. Consistent practice will solidify your understanding and build your confidence in tackling these types of problems.
Latest Posts
Latest Posts
-
What Is 25 25
Sep 24, 2025
-
6 5 5 6
Sep 24, 2025
-
Signs Of Secure Attachment
Sep 24, 2025
-
Number Line To 10
Sep 24, 2025
-
18 Km Per Hour
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 52/60 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.