56 Divided By 3
renascent
Sep 23, 2025 · 6 min read
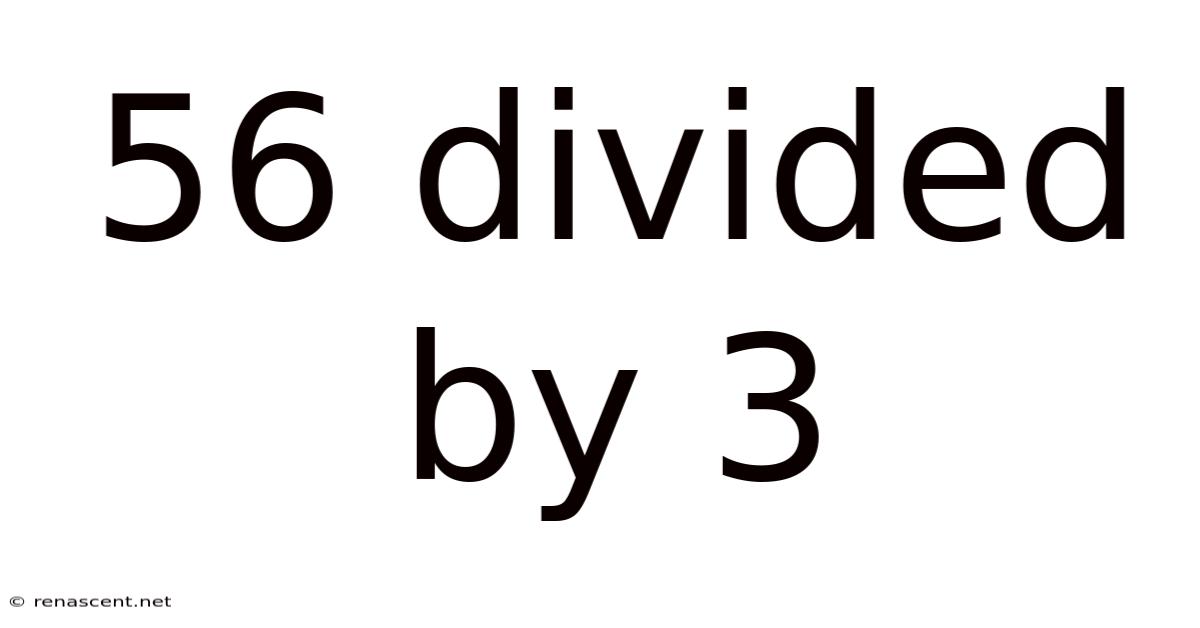
Table of Contents
Exploring the Division: 56 Divided by 3 – A Deep Dive into Division, Remainders, and Applications
Understanding division is fundamental to mathematics, and seemingly simple problems like "56 divided by 3" can unlock a deeper understanding of concepts crucial for advanced mathematical applications. This article will explore this specific division problem, explaining not just the answer but also the underlying principles, different methods for solving it, the significance of remainders, and real-world applications of division. We will also delve into related concepts to provide a comprehensive understanding of this basic yet important arithmetic operation.
Introduction: The Basics of Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts or groups. In the equation a ÷ b = c, 'a' is the dividend (the number being divided), 'b' is the divisor (the number dividing the dividend), and 'c' is the quotient (the result of the division).
When we consider 56 divided by 3 (56 ÷ 3), 56 is our dividend and 3 is our divisor. We are seeking the quotient that represents how many times 3 fits entirely into 56. This process often leads to a remainder, which represents the portion of the dividend that is left over after the division.
Calculating 56 Divided by 3: Step-by-Step Methods
There are several methods to calculate 56 ÷ 3:
1. Long Division: This is a standard algorithm taught in schools.
- Step 1: Divide the first digit of the dividend (5) by the divisor (3). 3 goes into 5 one time (1). Write the 1 above the 5.
- Step 2: Multiply the quotient (1) by the divisor (3): 1 x 3 = 3. Write the 3 below the 5.
- Step 3: Subtract the result (3) from the digit above it (5): 5 - 3 = 2.
- Step 4: Bring down the next digit of the dividend (6), placing it next to the 2 to create the number 26.
- Step 5: Divide 26 by 3. 3 goes into 26 eight times (8). Write the 8 above the 6.
- Step 6: Multiply the quotient (8) by the divisor (3): 8 x 3 = 24. Write the 24 below the 26.
- Step 7: Subtract the result (24) from 26: 26 - 24 = 2. This is the remainder.
Therefore, 56 ÷ 3 = 18 with a remainder of 2. We can express this as 18 R2 or 18 2/3.
2. Repeated Subtraction: This method involves repeatedly subtracting the divisor from the dividend until the result is less than the divisor.
- 56 - 3 = 53
- 53 - 3 = 50
- 50 - 3 = 47
- ...and so on until you reach a number less than 3.
Counting how many times you subtracted 3 will give you the quotient. The remaining number is the remainder. This method is conceptually simple but can be tedious for larger numbers.
3. Using Fractions: The remainder can be expressed as a fraction. The remainder (2) becomes the numerator, and the divisor (3) becomes the denominator. This gives us the mixed number 18 2/3. This fraction can also be converted to a decimal (approximately 18.666...).
Understanding Remainders: Their Significance and Interpretation
The remainder in 56 ÷ 3 is 2. This remainder is crucial because it shows that 56 cannot be perfectly divided into groups of 3. It represents the leftover quantity after forming as many groups of 3 as possible.
Remainders are not just leftovers; they provide vital information in various contexts:
- Real-world applications: If you have 56 candies and want to divide them equally among 3 friends, each friend gets 18 candies, and you have 2 candies left over.
- Modular arithmetic: Remainders are fundamental in modular arithmetic, a branch of number theory with applications in cryptography and computer science. The remainder when a number is divided by another number is called the modulo operation (e.g., 56 mod 3 = 2).
- Cyclic patterns: Remainders can help identify cyclic patterns and repetitions in sequences.
Real-World Applications of Division and Remainders
The seemingly simple division problem 56 ÷ 3 has broad practical applications:
- Resource allocation: Dividing resources equally (e.g., assigning tasks, distributing materials).
- Measurement and conversion: Converting units (e.g., converting inches to feet).
- Pricing and discounts: Calculating unit prices and discounts.
- Average and statistics: Calculating average values and statistical measures.
- Scheduling and planning: Organizing schedules and planning events.
- Computer science: Used extensively in algorithms, data structures, and cryptography.
Exploring Related Concepts: Factors, Multiples, and Divisibility Rules
Understanding 56 ÷ 3 leads us to related mathematical concepts:
- Factors: Factors of a number are the integers that divide it without leaving a remainder. The factors of 56 are 1, 2, 4, 7, 8, 14, 28, and 56. 3 is not a factor of 56.
- Multiples: Multiples of a number are the products obtained by multiplying that number by integers. Multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30... and so on. 56 is not a multiple of 3.
- Divisibility rules: Divisibility rules are shortcuts to determine whether a number is divisible by another number without performing long division. For instance, a number is divisible by 3 if the sum of its digits is divisible by 3. The sum of the digits of 56 (5+6=11) is not divisible by 3, confirming that 56 is not divisible by 3.
Frequently Asked Questions (FAQ)
Q: What is the exact decimal value of 56 ÷ 3?
A: The exact decimal value is a repeating decimal: 18.66666... It can be represented as 18.6̅.
Q: Can you explain the concept of a remainder in simpler terms?
A: Imagine you have 56 cookies and you want to put them into bags of 3 cookies each. You can fill 18 bags completely, but you will have 2 cookies left over. Those 2 cookies are the remainder.
Q: Are there any other ways to represent the result of 56 ÷ 3?
A: Yes, besides 18 R2 and 18 2/3, you can represent it as the decimal 18.6̅ or using other mathematical notations depending on the context.
Q: Why is understanding remainders important?
A: Remainders tell us when a division is not exact and help us understand the leftover quantity. This is crucial in many real-world applications, from resource allocation to advanced mathematical concepts.
Conclusion: Beyond the Answer – Understanding the Process
This in-depth exploration of "56 divided by 3" demonstrates that understanding a simple division problem goes far beyond obtaining the answer. It involves grasping the fundamental principles of division, the significance of remainders, and the connections to other mathematical concepts. The ability to perform and interpret division, including handling remainders, is a cornerstone of mathematical literacy and has wide-ranging practical applications in various fields. By understanding the process, we build a stronger foundation for more complex mathematical challenges. The seemingly simple act of dividing 56 by 3 unlocks a wealth of mathematical knowledge and its real-world applications.
Latest Posts
Latest Posts
-
Electrons In Carbon Atom
Sep 23, 2025
-
30 Out Of 32
Sep 23, 2025
-
Model Lock And Key
Sep 23, 2025
-
Electron Configuration For Mg
Sep 23, 2025
-
1 3 Improper Fraction
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 56 Divided By 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.