6/20 As A Percentage
renascent
Sep 22, 2025 · 5 min read
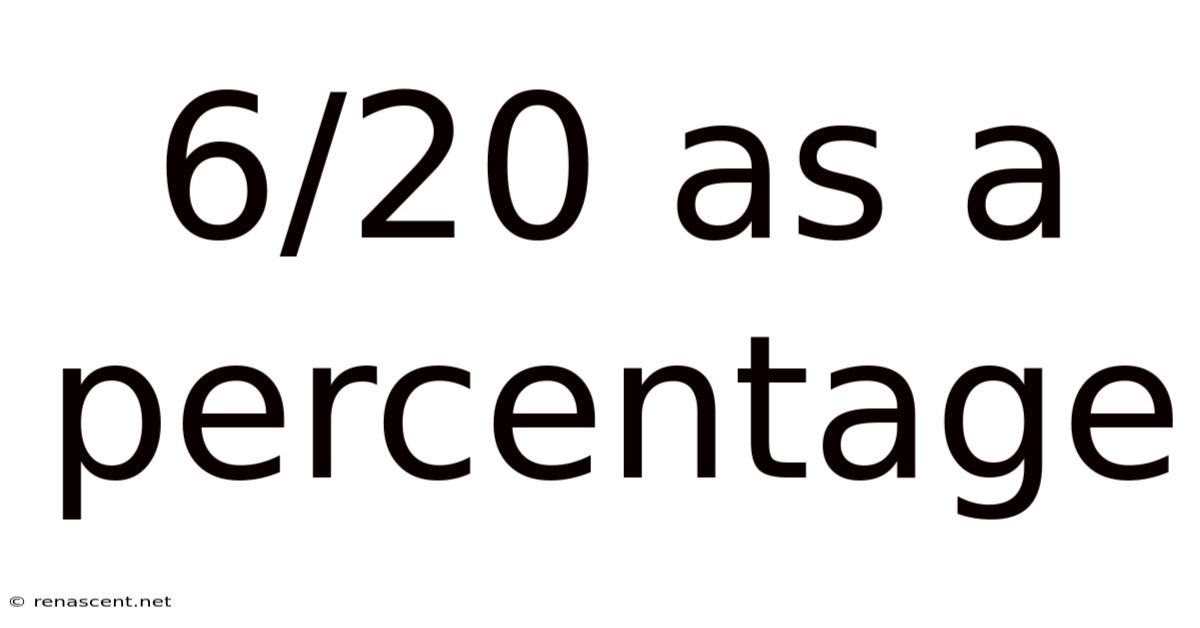
Table of Contents
6/20 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with widespread applications in daily life, from calculating discounts to understanding financial reports. This comprehensive guide will delve deep into converting the fraction 6/20 into a percentage, exploring the underlying concepts, different methods of calculation, and practical applications. We will also address frequently asked questions and provide further exercises to solidify your understanding. This will equip you with the knowledge to confidently tackle similar fraction-to-percentage conversions in the future.
Understanding Fractions and Percentages
Before diving into the specifics of 6/20, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It's composed of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates how many parts make up the whole.
A percentage, on the other hand, represents a fraction out of 100. The word "percent" literally means "out of 100" ( per cent ). Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or 1/2. Converting fractions to percentages involves finding an equivalent fraction with a denominator of 100, or using a more direct method involving division.
Method 1: Converting the Fraction Directly
The most straightforward method to convert 6/20 to a percentage is to first simplify the fraction and then convert it to a percentage.
1. Simplify the Fraction:
We can simplify the fraction 6/20 by finding the greatest common divisor (GCD) of both the numerator and the denominator. The GCD of 6 and 20 is 2. Dividing both the numerator and denominator by 2, we get:
6 ÷ 2 = 3 20 ÷ 2 = 10
So, 6/20 simplifies to 3/10.
2. Convert the Simplified Fraction to a Percentage:
To convert 3/10 to a percentage, we need to find an equivalent fraction with a denominator of 100. We can achieve this by multiplying both the numerator and the denominator by 10:
3 × 10 = 30 10 × 10 = 100
This gives us the equivalent fraction 30/100. Since a percentage is a fraction out of 100, 30/100 is equal to 30%.
Therefore, 6/20 as a percentage is 30%.
Method 2: Using Decimal Conversion
Another common approach is to first convert the fraction to a decimal and then convert the decimal to a percentage.
1. Convert the Fraction to a Decimal:
To convert 6/20 to a decimal, we divide the numerator (6) by the denominator (20):
6 ÷ 20 = 0.3
2. Convert the Decimal to a Percentage:
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percent sign (%):
0.3 × 100 = 30
Therefore, 0.3 is equal to 30%. Again, we arrive at the same answer: 6/20 is equivalent to 30%.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve for the percentage. We can set up a proportion:
6/20 = x/100
Where 'x' represents the percentage we want to find. To solve for x, we cross-multiply:
20x = 600
Then, divide both sides by 20:
x = 600 ÷ 20 = 30
Therefore, x = 30, meaning 6/20 is 30%.
Real-World Applications of Percentage Conversions
Understanding how to convert fractions to percentages is crucial in various real-life situations:
-
Calculating Discounts: If a store offers a 30% discount on an item, you can easily calculate the discount amount by converting the percentage to a fraction (30/100 = 3/10) and multiplying it by the item's original price.
-
Financial Calculations: Interest rates, tax calculations, profit margins, and investment returns are all expressed as percentages. Understanding percentage conversions allows you to easily compare and analyze different financial options.
-
Scientific Data Analysis: In scientific studies, data is often represented as percentages to show the proportion of different outcomes or observations within a sample.
-
Grade Calculations: Academic grades are frequently expressed as percentages, making it easy to track your progress and overall academic performance.
-
Survey Results: Results from surveys and polls are commonly presented as percentages to represent the proportion of respondents who chose each option.
Frequently Asked Questions (FAQ)
Q1: Can I use a calculator to convert fractions to percentages?
A1: Yes, most calculators have a percentage function that can directly convert fractions to percentages. Simply enter the fraction (e.g., 6/20) and press the percentage button.
Q2: What if the fraction is an improper fraction (numerator > denominator)?
A2: An improper fraction will result in a percentage greater than 100%. Convert the improper fraction to a mixed number, convert the fractional part to a percentage as described above and add it to 100%. For instance, if you have the improper fraction 20/6, converting to a mixed number would give 3 2/6 (or 3 1/3). Then convert 1/3 to a percentage (approximately 33.33%) and add it to 100% (giving you approximately 133.33%).
Q3: Are there any other ways to calculate percentages from fractions?
A3: You can also utilize online percentage calculators or spreadsheets which often have built-in functions to convert fractions to percentages efficiently.
Conclusion
Converting fractions to percentages is a fundamental mathematical skill applicable in countless everyday scenarios. We've explored three different methods for converting 6/20 to a percentage, consistently arriving at the answer of 30%. Whether you use direct conversion, decimal conversion, or proportions, understanding the underlying principles will allow you to confidently tackle various percentage calculations in your academic pursuits and daily life. Mastering this skill opens doors to comprehending a wide range of mathematical and real-world problems involving proportions and ratios. Remember to practice regularly to strengthen your understanding and efficiency in tackling such conversions.
Latest Posts
Latest Posts
-
Ultimate Tensile Strength Formula
Sep 22, 2025
-
Dilation From Y Axis
Sep 22, 2025
-
5 12 As A Percent
Sep 22, 2025
-
Mole To Mole Relationship
Sep 22, 2025
-
What Are Condensation Reactions
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 6/20 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.