6 25 As Percent
renascent
Sep 22, 2025 · 5 min read
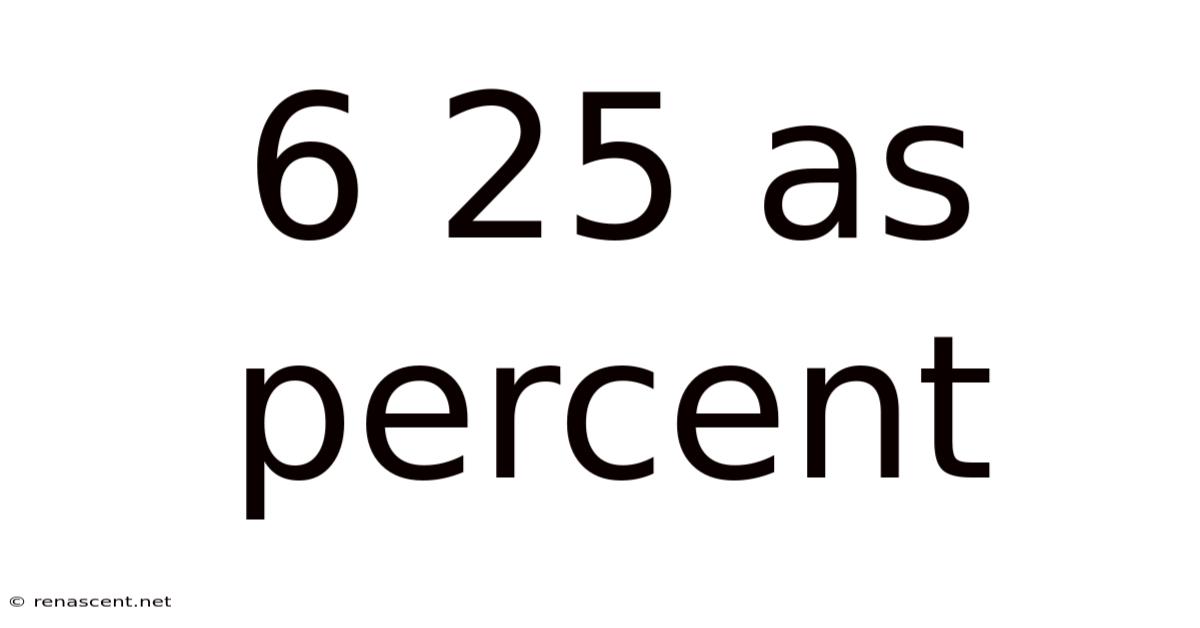
Table of Contents
Understanding 6/25 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced statistical analysis. This comprehensive guide will delve into the process of converting the fraction 6/25 into a percentage, explaining the methodology in detail and exploring related concepts. We'll not only show you how to do it but also why it works, ensuring a thorough understanding. This guide is designed for learners of all levels, from those just starting to grasp fractions to those seeking a deeper understanding of percentage conversions.
Understanding Fractions and Percentages
Before we dive into converting 6/25, let's briefly review the core concepts of fractions and percentages.
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of parts in the whole.
A percentage, denoted by the symbol %, represents a fraction of 100. It essentially expresses a proportion out of 100. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Method 1: Converting the Fraction to a Decimal, Then to a Percentage
This is the most common and arguably the easiest method for converting a fraction to a percentage. It involves two simple steps:
Step 1: Convert the fraction to a decimal.
To convert a fraction to a decimal, we divide the numerator by the denominator. In our case:
6 ÷ 25 = 0.24
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%).
0.24 × 100 = 24%
Therefore, 6/25 is equal to 24%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method involves finding an equivalent fraction where the denominator is 100. Since percentages are based on 100, this directly gives us the percentage.
Step 1: Determine the multiplier.
We need to find a number that, when multiplied by the denominator (25), equals 100. In this case:
100 ÷ 25 = 4
Therefore, we need to multiply both the numerator and the denominator by 4.
Step 2: Multiply the numerator and the denominator.
6 × 4 = 24 25 × 4 = 100
This gives us the equivalent fraction: 24/100.
Step 3: Express as a percentage.
Since the denominator is 100, the numerator directly represents the percentage:
24/100 = 24%
Again, we find that 6/25 is equal to 24%.
Method 3: Using Proportions
This method uses the concept of proportions to solve for the percentage. It's a more formal approach, often used in advanced mathematical contexts.
We can set up a proportion:
6/25 = x/100
Where 'x' represents the percentage we're trying to find.
To solve for 'x', we can cross-multiply:
25x = 600
Then, divide both sides by 25:
x = 600 ÷ 25 = 24
Therefore, x = 24, meaning 6/25 is equal to 24%.
Why These Methods Work: A Deeper Look
All three methods are fundamentally based on the same principle: the relationship between fractions, decimals, and percentages. They are simply different approaches to expressing and manipulating this relationship.
The first method leverages the direct conversion between fractions and decimals through division, followed by the simple multiplication by 100 to obtain the percentage. This method is intuitive and easily applicable.
The second method highlights the core definition of a percentage as a fraction out of 100. By finding an equivalent fraction with a denominator of 100, we directly obtain the percentage. This method reinforces the fundamental understanding of percentages.
The third method utilizes the powerful tool of proportions, demonstrating how equivalent ratios can be used to solve for unknown values. This method is more versatile and can be applied to more complex percentage problems.
Practical Applications of Percentage Conversions
Understanding how to convert fractions to percentages is essential in numerous real-world scenarios. Here are a few examples:
- Calculating discounts: If a store offers a 25% discount on an item, you can use this knowledge to calculate the discount amount.
- Determining grades: Many academic grading systems use percentages to represent student performance. Converting fractional scores to percentages is crucial for understanding grades.
- Analyzing data: In statistics and data analysis, percentages are frequently used to represent proportions and probabilities. Converting fractions to percentages is essential for interpreting these data.
- Financial calculations: Interest rates, tax calculations, and investment returns are often expressed as percentages. Understanding percentage conversions is crucial for financial literacy.
- Everyday life: Tipping in restaurants, calculating sales tax, and understanding nutritional information on food labels often involve percentage calculations.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to convert 6/25 to a percentage?
A: Absolutely! Most calculators have a percentage function that can directly convert fractions or decimals to percentages. Simply divide 6 by 25 and then use the percentage function.
Q: What if the fraction has a larger numerator than denominator?
A: If the numerator is larger than the denominator, the resulting percentage will be greater than 100%. This indicates a value more than the whole. The conversion process remains the same: divide the numerator by the denominator and multiply by 100.
Q: Are there any other methods to convert fractions to percentages?
A: While the methods described above are the most common and straightforward, other advanced mathematical techniques can also be used, especially for more complex fractions.
Q: Why is understanding percentages important?
A: Percentages provide a standardized and easily understandable way to represent proportions. This makes comparing and interpreting data across different contexts much simpler. It's a fundamental concept across various disciplines.
Conclusion
Converting 6/25 to a percentage is a straightforward process achievable through various methods. Understanding the underlying principles, whether through direct decimal conversion, equivalent fraction creation, or proportion usage, is key to mastering this fundamental skill. The ability to effortlessly convert fractions to percentages is not merely a mathematical skill; it's a vital tool for navigating various aspects of daily life, from financial management to data interpretation. Mastering this concept empowers you with a crucial skill for success in academic pursuits and beyond. Practice makes perfect, so keep practicing these methods with different fractions to solidify your understanding.
Latest Posts
Latest Posts
-
20 Of 1 3 Million
Sep 22, 2025
-
70 Miles Per Hour
Sep 22, 2025
-
1300 Divided By 5
Sep 22, 2025
-
Masque Meaning In Tempest
Sep 22, 2025
-
55 Knots To Km
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 6 25 As Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.