6/4 As A Percentage
renascent
Sep 23, 2025 · 6 min read
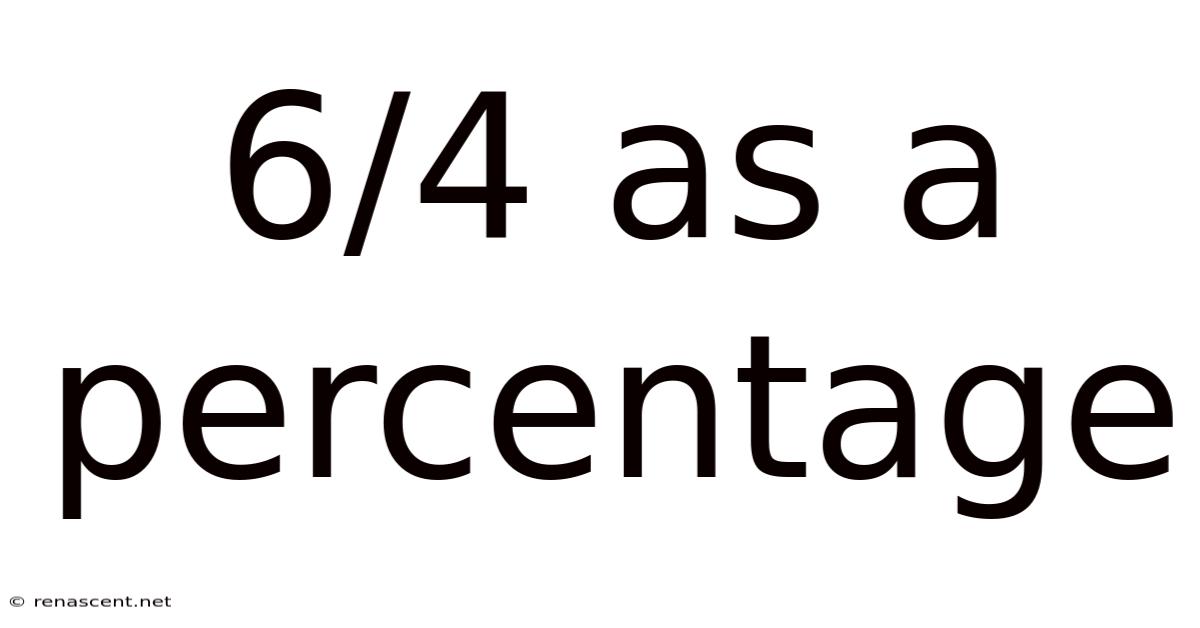
Table of Contents
Understanding 6/4 as a Percentage: A Comprehensive Guide
Representing fractions as percentages is a fundamental skill in mathematics with broad applications in everyday life, from calculating discounts and interest rates to understanding statistical data and expressing proportions. This article provides a comprehensive guide to understanding how to convert the fraction 6/4 into a percentage, exploring the underlying concepts and providing practical examples. We will delve into the process step-by-step, clarifying any potential confusion and demonstrating the versatility of percentage calculations. This guide will equip you with the knowledge to tackle similar fractional conversions with confidence.
Introduction: Fractions, Decimals, and Percentages – The Interconnected Trio
Before diving into the conversion of 6/4 to a percentage, let's briefly review the relationships between fractions, decimals, and percentages. These three representational forms are interchangeable, each offering a unique way to express a portion of a whole.
-
Fractions: Fractions express a part of a whole using a numerator (top number) and a denominator (bottom number). For instance, 6/4 represents 6 parts out of a total of 4 parts. This indicates a quantity greater than one whole.
-
Decimals: Decimals represent parts of a whole using base-10 notation. They are essentially fractions where the denominator is a power of 10 (10, 100, 1000, etc.).
-
Percentages: Percentages express parts of a whole as a fraction of 100. The symbol "%" denotes "per hundred," meaning "out of 100."
The ability to convert between these forms is crucial for various mathematical operations and real-world applications.
Step-by-Step Conversion of 6/4 to a Percentage
Converting 6/4 to a percentage involves a straightforward process:
Step 1: Convert the Fraction to a Decimal
The first step is to convert the improper fraction 6/4 into a decimal. To do this, we perform the division: 6 divided by 4.
6 ÷ 4 = 1.5
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%).
1.5 x 100 = 150
Therefore, 1.5 as a percentage is 150%.
Step 3: Understanding the Result
The result, 150%, signifies that 6/4 represents 150% of one whole. This is because 6/4 is an improper fraction, meaning the numerator is larger than the denominator. It represents more than one whole unit. If we visualize this with, for example, pizzas, 6/4 means we have 1 and a half pizzas when we expected only one whole pizza.
Alternative Method: Using Equivalent Fractions
Another way to approach this conversion is by using equivalent fractions. We can simplify the improper fraction 6/4 first:
6/4 can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 2.
6 ÷ 2 = 3 4 ÷ 2 = 2
This simplifies the fraction to 3/2. Now, we can convert 3/2 to a decimal:
3 ÷ 2 = 1.5
Following the same steps as before, we multiply the decimal by 100 to get the percentage:
1.5 x 100 = 150%
This method demonstrates that simplifying the fraction beforehand doesn't affect the final percentage. The result remains 150%.
Practical Applications of Percentage Conversions
Understanding how to convert fractions to percentages is crucial in numerous real-world situations:
-
Finance: Calculating interest rates, profit margins, discounts, and tax rates. For example, a 150% increase in investment value means the investment's value has more than doubled.
-
Statistics: Representing proportions and probabilities. Data is often expressed as percentages to facilitate easy comparison and interpretation.
-
Science: Expressing experimental results, such as the percentage yield of a chemical reaction.
-
Everyday Life: Calculating tips, determining sale prices, and understanding proportions in recipes or construction projects.
Dealing with Different Types of Fractions
The process of converting fractions to percentages remains consistent regardless of whether the fraction is proper (numerator < denominator), improper (numerator > denominator), or mixed (a whole number and a fraction).
-
Proper Fractions: These fractions, like 1/4, result in percentages less than 100%.
-
Improper Fractions: As shown with 6/4, these fractions result in percentages greater than 100%.
-
Mixed Numbers: To convert a mixed number like 1 1/2 to a percentage, first convert it to an improper fraction (3/2), then follow the steps outlined above.
Further Exploration: Percentage Increase and Decrease
Understanding percentages extends beyond simple conversions. Calculating percentage increase or decrease requires additional steps.
Percentage Increase: This calculates the increase relative to the original value. For instance, if a value increases from 100 to 150, the percentage increase is calculated as follows:
(150 - 100) / 100 x 100% = 50%
Percentage Decrease: This calculates the decrease relative to the original value. If a value decreases from 150 to 100, the percentage decrease is:
(150 - 100) / 150 x 100% ≈ 33.33%
Frequently Asked Questions (FAQ)
Q1: Can I convert a fraction to a percentage without first converting it to a decimal?
A1: While the decimal conversion method is widely used and often the most straightforward, you can convert directly. For example, with the fraction 6/4, you can set up a proportion: 6/4 = x/100. Solving for x will give you the percentage.
Q2: What if the decimal has many digits after the decimal point?
A2: Round the decimal to an appropriate number of decimal places depending on the required accuracy. For instance, if you get 1.5555..., you might round to 1.56 before converting to a percentage (156%).
Q3: How do I handle negative fractions and percentages?
A3: Negative fractions represent negative values. When converting a negative fraction to a percentage, simply convert the fraction's absolute value to a percentage and then add a negative sign to the result.
Q4: What are some common mistakes to avoid when converting fractions to percentages?
A4: Common errors include forgetting to multiply by 100, incorrectly calculating the decimal equivalent of the fraction, and misinterpreting the meaning of percentages greater than 100%. Always double-check your calculations and ensure you understand the context of the percentage.
Conclusion: Mastering Percentage Conversions
Converting fractions like 6/4 to percentages is a valuable skill with wide-ranging applications. By understanding the relationship between fractions, decimals, and percentages, and by following the systematic steps outlined in this guide, you can confidently handle these conversions. Remember to practice regularly, exploring different types of fractions and practicing percentage increase and decrease calculations. With consistent practice, you'll master this fundamental mathematical concept and apply it effectively across various domains. The ability to seamlessly translate between these different forms of representation is a key element of mathematical fluency and a valuable tool for problem-solving in many fields.
Latest Posts
Latest Posts
-
4 3 Inches In Cm
Sep 23, 2025
-
Is Study Fetch Free
Sep 23, 2025
-
New York Ny Latitude
Sep 23, 2025
-
1 12 As A Decimal
Sep 23, 2025
-
Dr Catherine Harris Medicare
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 6/4 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.