60 Divided By 10
renascent
Sep 21, 2025 · 5 min read
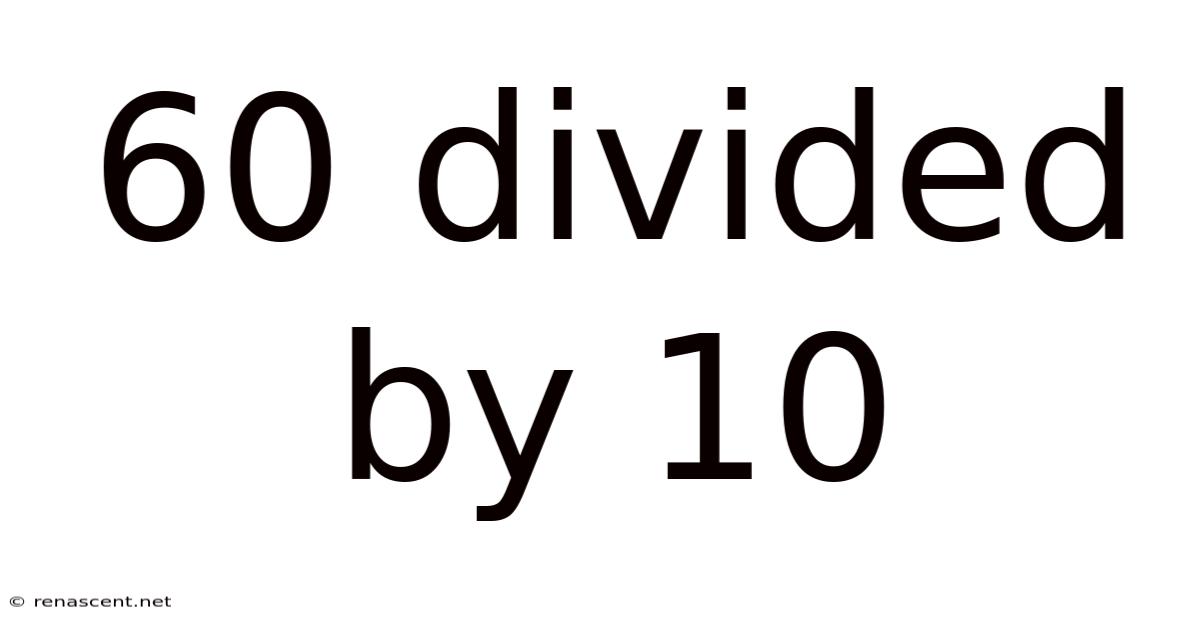
Table of Contents
60 Divided by 10: A Deep Dive into Division and its Applications
This article explores the seemingly simple calculation of 60 divided by 10, delving far beyond the immediate answer. We'll examine the underlying principles of division, explore different methods for solving this problem, and discuss its real-world applications, demonstrating the significance of this fundamental arithmetic operation. Understanding division is crucial for a solid foundation in mathematics and its widespread applications in various fields. This exploration will cater to all levels, from elementary school students grasping the concept of division to those seeking a deeper understanding of its mathematical underpinnings.
Understanding Division: The Basics
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It's essentially the process of splitting a quantity into equal parts. In the context of 60 divided by 10, we're asking: "How many times does 10 go into 60?" or "If we divide 60 into 10 equal groups, how many items are in each group?"
The expression "60 divided by 10" can be written in several ways:
- 60 ÷ 10
- 60 / 10
- 60 ¹⁰⁄₁₀
All these notations represent the same mathematical operation.
Solving 60 Divided by 10: Various Methods
There are several ways to solve this division problem, each offering a unique approach to understanding the concept:
1. Repeated Subtraction: We can repeatedly subtract 10 from 60 until we reach 0. The number of times we subtract 10 represents the answer.
60 - 10 = 50 50 - 10 = 40 40 - 10 = 30 30 - 10 = 20 20 - 10 = 10 10 - 10 = 0
We subtracted 10 six times, therefore, 60 ÷ 10 = 6.
2. Using Multiplication Tables: Knowing our multiplication tables is a quick way to solve this. We ask ourselves: "What number multiplied by 10 equals 60?" The answer, from our knowledge of multiplication facts, is 6.
3. Long Division: While seemingly overkill for this simple problem, long division is a crucial method for more complex division problems. Setting it up:
6
10|60
-60
0
We determine how many times 10 goes into 60 (6 times), multiply 10 by 6 (60), and subtract the result from 60, leaving a remainder of 0.
4. Conceptual Understanding with Objects: Imagine you have 60 apples, and you want to divide them equally among 10 friends. You'd give each friend 6 apples. This visual representation helps solidify the concept of division.
The Answer: 6
Regardless of the method used, the answer to 60 divided by 10 is always 6. This simple equation forms the bedrock for understanding more complex mathematical concepts.
Beyond the Calculation: Real-World Applications
The seemingly simple calculation of 60 divided by 10 has far-reaching implications across numerous real-world scenarios:
1. Everyday Life:
- Sharing: Dividing resources fairly among a group of people. If 60 candies are to be shared among 10 children, each child receives 6 candies.
- Measurement Conversions: Converting units of measurement. For example, converting 60 centimeters to meters (100 centimeters = 1 meter), you'd divide 60 by 100 to get 0.6 meters.
- Pricing: Calculating the cost per unit. If 10 apples cost 60 dollars, each apple costs 6 dollars.
- Recipe Scaling: Adjusting recipes based on the number of servings. If a recipe for 10 servings requires 60 grams of flour, then a recipe for 1 serving requires 6 grams of flour.
2. Business and Finance:
- Profit Sharing: Dividing profits among partners or shareholders.
- Cost Analysis: Determining the cost per unit of production.
- Inventory Management: Tracking stock levels and calculating average daily sales.
- Financial Ratios: Calculating key financial metrics, such as return on investment (ROI).
3. Science and Engineering:
- Data Analysis: Calculating averages, means, and proportions.
- Physics: Solving problems involving velocity, acceleration, and force.
- Chemistry: Determining molar masses and concentrations.
- Engineering: Designing structures and systems with appropriate scaling and proportions.
4. Computer Science:
- Algorithm Design: Developing efficient algorithms for data processing and manipulation.
- Data Structures: Managing and organizing data in efficient ways.
- Memory Allocation: Dividing memory resources among different processes.
These are just a few examples. The principle of dividing a quantity into equal parts underpins numerous calculations and decision-making processes across various fields. Understanding this fundamental concept is essential for navigating these complex situations effectively.
Exploring Further: Division with Remainders
While 60 divided by 10 results in a whole number (6), many division problems result in remainders. For instance, if we were to divide 67 by 10:
6 R 7
10|67
-60
7
This means that 10 goes into 67 six times, with a remainder of 7. Understanding remainders is crucial for solving more complex division problems and applying them to real-world scenarios where exact divisions might not always be possible.
Frequently Asked Questions (FAQ)
Q1: What happens if I divide a smaller number by a larger number?
A1: If you divide a smaller number by a larger number, the result will be a decimal or a fraction less than 1. For instance, 10 divided by 60 is 1/6 or approximately 0.1667.
Q2: What is the importance of understanding division?
A2: Understanding division is fundamental to solving a wide range of problems in mathematics and various real-world applications. It allows us to calculate proportions, ratios, averages, and shares, which are essential in everyday life, business, science, and many other fields.
Q3: Are there other ways to represent division besides the ones mentioned?
A3: Yes, division can also be represented using fractions (e.g., 60/10) and as a decimal (e.g., 6.0).
Q4: How can I improve my skills in division?
A4: Practice is key! Start with simple problems and gradually increase the difficulty. Use different methods to solve the problems and choose the one that best suits your understanding. Utilize online resources, worksheets, and educational apps to strengthen your skills.
Conclusion: The Enduring Power of Division
The seemingly simple calculation of 60 divided by 10 serves as a gateway to understanding the broader concept of division and its profound implications. From everyday tasks to complex scientific calculations, division is an indispensable tool that empowers us to solve problems, analyze data, and make informed decisions. Mastering this fundamental arithmetic operation is crucial for academic success and navigating the complexities of the real world. Its power lies not just in the answer (6), but in the understanding of the process itself and its widespread applications across various disciplines. Remember, a solid grasp of division provides a strong foundation for tackling more advanced mathematical concepts and real-world challenges.
Latest Posts
Latest Posts
-
28 Cm To Inches
Sep 21, 2025
-
Atacama Desert Map Location
Sep 21, 2025
-
13 20 As A Percent
Sep 21, 2025
-
Barium Sulfate Molar Mass
Sep 21, 2025
-
Polynomial Long Division Calc
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 60 Divided By 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.