685 Divided By 2
renascent
Sep 23, 2025 · 6 min read
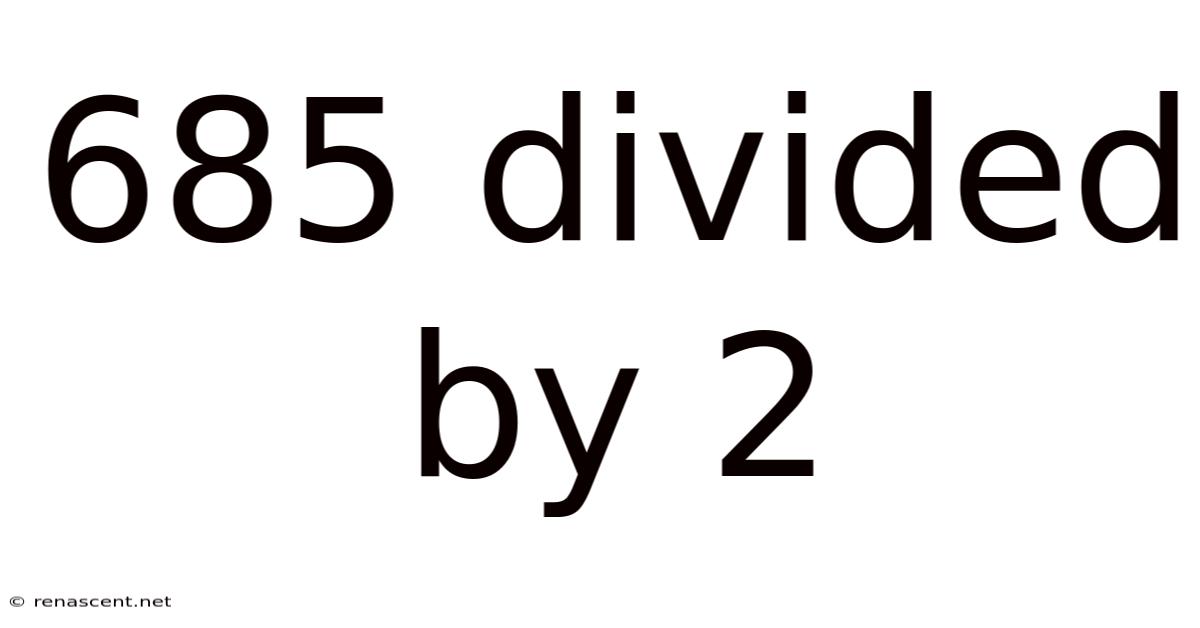
Table of Contents
685 Divided by 2: A Deep Dive into Division and Beyond
This article explores the seemingly simple problem of 685 divided by 2, but it goes far beyond a simple calculation. We'll delve into the mechanics of division, explore different methods for solving this problem, discuss the concept of remainders, and even touch upon the broader mathematical principles involved. Understanding this seemingly basic operation unlocks a gateway to more complex mathematical concepts. This guide is perfect for students, educators, and anyone curious about the beauty and practicality of arithmetic.
Introduction: Understanding Division
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts. In the case of 685 divided by 2 (written as 685 ÷ 2 or 685/2), we are asking: "How many times does 2 fit into 685?" The answer isn't a whole number, which leads us to an important concept: remainders.
Method 1: Long Division – The Classic Approach
Long division is a traditional method that systematically breaks down the division problem into smaller, manageable steps. Let's work through 685 ÷ 2:
-
Set up the problem: Write 685 inside the long division symbol (⟌) and 2 outside.
-
Divide the hundreds: How many times does 2 go into 6? It goes in 3 times (3 x 2 = 6). Write the 3 above the 6 in the hundreds place.
-
Subtract: Subtract 6 from 6, leaving 0.
-
Bring down the tens: Bring down the 8 (from the tens place) next to the 0.
-
Divide the tens: How many times does 2 go into 8? It goes in 4 times (4 x 2 = 8). Write the 4 above the 8 in the tens place.
-
Subtract: Subtract 8 from 8, leaving 0.
-
Bring down the ones: Bring down the 5 (from the ones place) next to the 0.
-
Divide the ones: How many times does 2 go into 5? It goes in 2 times (2 x 2 = 4). Write the 2 above the 5 in the ones place.
-
Subtract: Subtract 4 from 5, leaving 1.
-
Remainder: The 1 is the remainder. This means that 2 goes into 685 342 times with 1 left over.
Therefore, 685 ÷ 2 = 342 with a remainder of 1. We can also express this as a mixed number: 342 ½ or a decimal: 342.5.
Method 2: Repeated Subtraction
This method involves repeatedly subtracting the divisor (2) from the dividend (685) until you reach 0 or a number smaller than the divisor. While less efficient for larger numbers, it helps visually demonstrate the concept of division.
Start with 685:
- 685 - 2 = 683
- 683 - 2 = 681
- ...and so on until you reach a number less than 2.
Counting how many times you subtracted 2 would give you the quotient (342), and the remaining number would be the remainder (1). This method is more time-consuming but offers a concrete understanding of division’s iterative nature.
Method 3: Using Fractions and Decimals
We can represent the division as a fraction: 685/2. To convert this to a decimal, we perform the long division as shown in Method 1. The result, as we found, is 342.5. This decimal representation is particularly useful in applications where fractional parts are relevant, such as measuring lengths or weights.
Understanding Remainders
The remainder (1 in this case) is the amount left over after dividing as equally as possible. It signifies that the dividend (685) is not perfectly divisible by the divisor (2). Remainders are important because they represent the "extra" portion that doesn't fit into the equal groups.
Practical Applications
Division, and understanding remainders, has numerous practical applications in everyday life:
-
Sharing: Dividing candy, toys, or other items equally amongst friends. The remainder indicates any items that need to be shared differently or kept aside.
-
Measurement: Cutting a length of fabric into equal pieces. The remainder represents the extra fabric left over.
-
Cooking: Dividing ingredients for a recipe amongst multiple servings.
-
Finance: Splitting bills amongst individuals.
Expanding on the Concept: Divisibility Rules
Divisibility rules are shortcuts for determining if a number is divisible by another number without performing the actual division. While there isn't a specific divisibility rule for 2 that significantly simplifies this problem, knowing divisibility rules for other numbers is beneficial. For instance:
-
Divisibility by 2: A number is divisible by 2 if its last digit is even (0, 2, 4, 6, or 8). 685 is not divisible by 2 because its last digit (5) is odd.
-
Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3. 6 + 8 + 5 = 19, which is not divisible by 3.
-
Divisibility by 5: A number is divisible by 5 if its last digit is 0 or 5. 685 is divisible by 5 because its last digit is 5.
Advanced Concepts: Prime Factorization and Modular Arithmetic
Let's briefly touch upon some more advanced mathematical concepts related to division:
-
Prime Factorization: This involves breaking down a number into its prime factors (numbers divisible only by 1 and themselves). Understanding prime factorization helps in simplifying fractions and solving more complex problems. While not directly applicable to solving 685 ÷ 2, it's a fundamental concept in number theory.
-
Modular Arithmetic: This system deals with remainders after division. It's used extensively in cryptography and computer science. The remainder of 1 when 685 is divided by 2 is a key element in modular arithmetic.
Frequently Asked Questions (FAQ)
Q: Can 685 be divided by 2 without a remainder?
A: No, 685 cannot be divided by 2 without a remainder. This is because 685 is an odd number, and odd numbers are never perfectly divisible by 2.
Q: What is the most efficient way to divide 685 by 2?
A: For this specific problem, long division is relatively straightforward and efficient. For much larger numbers, calculators or computer programs would be more efficient.
Q: What if I want to divide 685 by a different number?
A: The same methods (long division, repeated subtraction, using fractions and decimals) can be applied to divide 685 by any other number.
Q: Why is understanding remainders important?
A: Remainders are crucial because they indicate the "leftover" portion when a division doesn't result in a whole number. This is vital in many real-world situations requiring equal distribution or precise measurements.
Conclusion: More Than Just Numbers
This seemingly simple problem of dividing 685 by 2 provides a gateway to understanding several important mathematical concepts. From the fundamental mechanics of long division to the broader applications of remainders and advanced topics like prime factorization and modular arithmetic, this exercise highlights the interconnectedness of mathematical ideas. Mastering division is not merely about getting the right answer; it’s about developing a deeper appreciation for the logic and elegance of mathematics. It is a building block for more complex mathematical explorations and a tool applicable in countless practical scenarios. Remember, the journey of mathematical understanding is a continuous process of exploration and discovery.
Latest Posts
Latest Posts
-
Ethanol To Ethanoic Acid
Sep 24, 2025
-
Myths About Mt Fuji
Sep 24, 2025
-
35th Wedding Anniversary Gifts
Sep 24, 2025
-
Can You Eat Blobfish
Sep 24, 2025
-
Metals That Are Ductile
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 685 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.