7/10 As A Decimal
renascent
Sep 22, 2025 · 5 min read
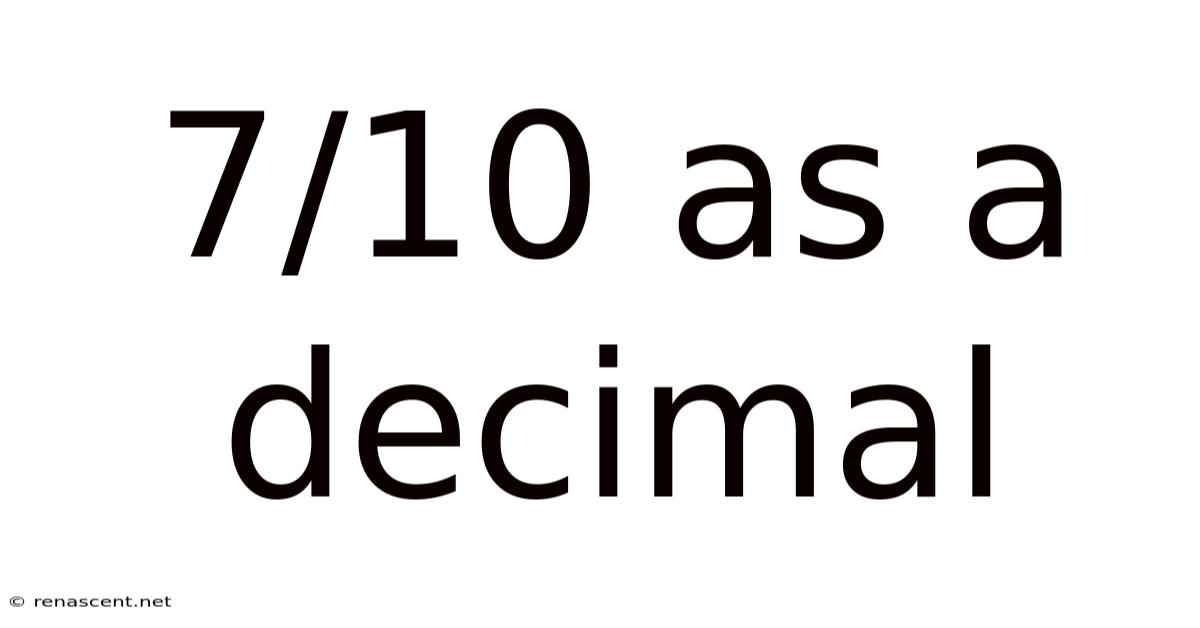
Table of Contents
7/10 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide explores the conversion of the fraction 7/10 to its decimal equivalent, explaining the process in detail and providing further insight into related concepts. Understanding this seemingly simple conversion lays the groundwork for mastering more complex fractional and decimal manipulations. We'll cover the basic method, delve into the underlying principles, and address frequently asked questions to ensure a complete understanding.
Understanding Fractions and Decimals
Before we delve into converting 7/10 to a decimal, let's refresh our understanding of fractions and decimals. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
A decimal, on the other hand, is a number expressed in the base-10 system, using a decimal point to separate the whole number part from the fractional part. Each digit to the right of the decimal point represents a power of ten (tenths, hundredths, thousandths, and so on).
Converting 7/10 to a Decimal: The Basic Method
The simplest way to convert 7/10 to a decimal is to recognize that the denominator is a power of 10 (10¹). This makes the conversion straightforward. We can simply write the numerator (7) and place the decimal point one place to the left, corresponding to the single zero in the denominator. Therefore, 7/10 as a decimal is 0.7.
Deeper Dive: The Division Method
While the direct method works well for fractions with denominators that are powers of 10, the division method is a more general approach applicable to all fractions. To convert a fraction to a decimal, we simply divide the numerator by the denominator.
In this case:
7 ÷ 10 = 0.7
This confirms our previous result. This method highlights the fundamental relationship between fractions and division: a fraction represents a division problem.
Understanding Place Value and Decimal Representation
Let's examine the place value system to further solidify our understanding. The number 0.7 can be broken down as follows:
- 0: Represents the whole number part (no whole units).
- 7: Represents seven-tenths (7/10).
This emphasizes that the digit after the decimal point represents the tenths place. If we had a fraction like 7/100, the decimal equivalent would be 0.07, with the 7 in the hundredths place.
Extending the Concept: Fractions with Different Denominators
While 7/10 was easily converted because the denominator was a power of 10, let's consider how to handle fractions with different denominators. For instance, consider the fraction 3/4. We can't directly convert this to a decimal using the shortcut method. Instead, we must use long division:
3 ÷ 4 = 0.75
Here, we find that 3/4 is equal to 0.75. This illustrates that the division method remains a reliable and universal technique for converting any fraction to its decimal equivalent.
Decimal Representation of Fractions: Terminating vs. Repeating Decimals
Converting fractions to decimals can result in two types of decimals: terminating and repeating.
-
Terminating decimals: These decimals have a finite number of digits after the decimal point. Examples include 0.7, 0.75, and 0.125. These typically arise from fractions whose denominators can be expressed as a product of powers of 2 and 5.
-
Repeating decimals (or recurring decimals): These decimals have an infinite number of digits after the decimal point, with a repeating pattern. For example, 1/3 = 0.3333... (the 3 repeats infinitely), and 1/7 = 0.142857142857... (the sequence 142857 repeats infinitely). These often result from fractions with denominators that are not factors of powers of 2 or 5.
Practical Applications of Decimal Conversions
The ability to convert fractions to decimals is vital in various practical applications:
-
Financial calculations: Calculating percentages, interest rates, and discounts often involve working with fractions and decimals.
-
Measurement and engineering: Precise measurements are frequently expressed using decimal notation.
-
Scientific calculations: Many scientific formulas and computations utilize decimal representations of numbers.
-
Data analysis and statistics: Working with datasets often necessitates converting fractions to decimals for easier manipulation and interpretation.
Frequently Asked Questions (FAQ)
Q1: Can all fractions be expressed as decimals?
A: Yes, all fractions can be expressed as decimals. The resulting decimal might be terminating or repeating.
Q2: Is there a way to quickly convert fractions with denominators other than powers of 10?
A: While the direct method is easiest for powers of 10, the division method is the most versatile and works for all fractions. Alternatively, you might be able to simplify the fraction first to make the division simpler. For example, 6/12 simplifies to 1/2 which is easily converted to 0.5
Q3: How do I handle repeating decimals?
A: Repeating decimals can be represented using a bar over the repeating sequence (e.g., 0.3̅3̅ for 1/3). In calculations, you might round the decimal to a certain number of places depending on the required accuracy.
Q4: What if the numerator is larger than the denominator?
A: If the numerator is larger than the denominator, the resulting decimal will be greater than 1. For example, 11/10 = 1.1. You can perform the division as usual and the result will be a decimal number greater than 1.
Q5: Are there any online tools or calculators to help with this conversion?
A: Yes, numerous online calculators and tools are available to convert fractions to decimals. However, understanding the underlying principles is crucial for mathematical proficiency.
Conclusion
Converting 7/10 to its decimal equivalent, 0.7, is a straightforward process that demonstrates a fundamental concept in mathematics. Whether using the direct method (for powers of 10) or the division method (applicable to all fractions), understanding the relationship between fractions and decimals is essential for tackling more complex mathematical problems. Mastering this skill opens doors to a wider range of applications across various disciplines. From simple everyday calculations to complex scientific computations, the ability to confidently convert fractions to decimals is an invaluable asset. Remember to practice regularly to build proficiency and confidence in your mathematical skills.
Latest Posts
Latest Posts
-
Poems That Use Consonance
Sep 22, 2025
-
Ultimate Tensile Strength Formula
Sep 22, 2025
-
Dilation From Y Axis
Sep 22, 2025
-
5 12 As A Percent
Sep 22, 2025
-
Mole To Mole Relationship
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 7/10 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.