7/12 To A Decimal
renascent
Sep 24, 2025 · 5 min read
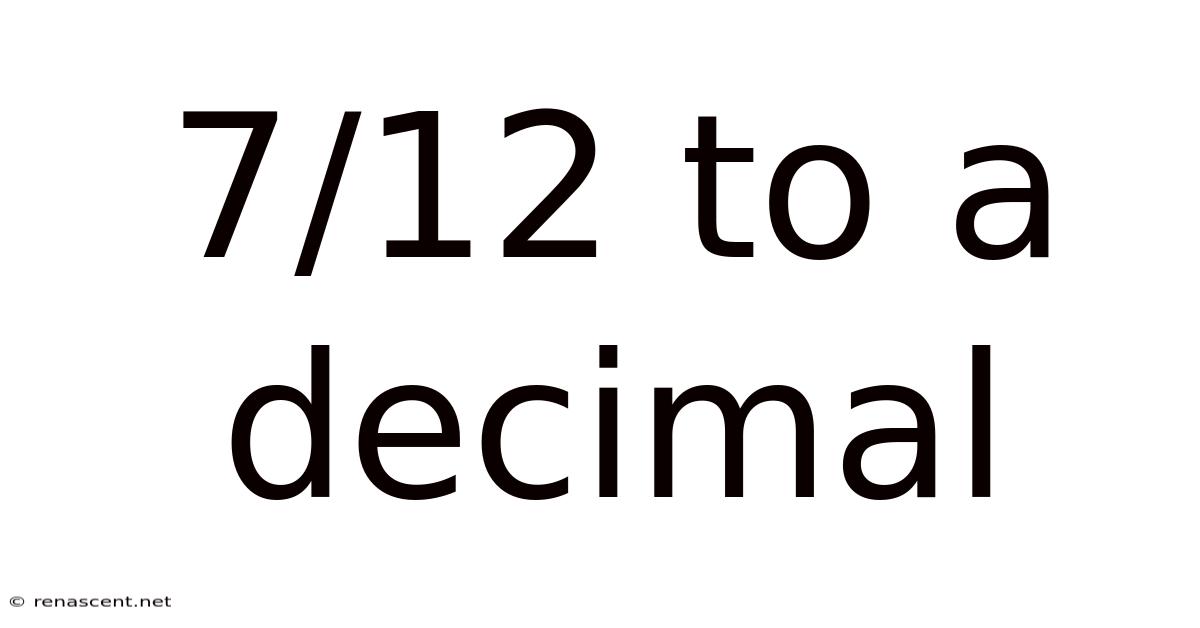
Table of Contents
Converting 7/12 to a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will walk you through the process of converting the fraction 7/12 to its decimal equivalent, exploring different methods and providing a deeper understanding of the underlying concepts. We will also delve into the significance of this conversion and its practical applications.
Introduction: Understanding Fractions and Decimals
Before we dive into converting 7/12, let's briefly review the basics of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). For instance, in the fraction 7/12, 7 is the numerator and 12 is the denominator. This means we have 7 parts out of a total of 12 equal parts.
A decimal, on the other hand, represents a number using a base-ten system, where the position of each digit relative to the decimal point determines its value. For example, 0.5 represents 5 tenths, and 0.25 represents 2 tenths and 5 hundredths. Converting a fraction to a decimal means expressing that fractional part as a decimal number.
Method 1: Long Division
The most straightforward method for converting a fraction to a decimal is through long division. This involves dividing the numerator by the denominator.
To convert 7/12 to a decimal, we divide 7 by 12:
0.58333...
12 | 7.00000
-60
100
- 96
40
-36
40
-36
40
-36
...
As you can see, the division results in a repeating decimal: 0.58333... The digit 3 repeats infinitely. This is often represented as 0.583̅ or 0.583. The bar above the 3 indicates the repeating digit.
Method 2: Using a Calculator
A simpler approach is to use a calculator. Simply enter 7 ÷ 12 and the calculator will provide the decimal equivalent. While convenient, understanding the long division method is crucial for grasping the underlying mathematical principles.
Method 3: Finding Equivalent Fractions
Sometimes, converting to a decimal becomes easier by first finding an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, etc.). Unfortunately, this method isn't directly applicable to 7/12, as 12 doesn't have any factors that can easily lead to a power of 10 denominator. However, understanding this technique is beneficial for other fraction conversions. For example, if you had the fraction 3/4, you could convert it to 75/100 (by multiplying both numerator and denominator by 25), which is easily represented as the decimal 0.75.
Understanding Repeating Decimals
The conversion of 7/12 results in a repeating decimal. This is because the fraction's denominator (12) contains prime factors other than 2 and 5. Only fractions with denominators that are composed solely of factors of 2 and 5 (or are multiples thereof) will convert to terminating decimals (decimals that end). For example, 1/4 (denominator is 2²) converts to 0.25, while 1/5 (denominator is 5) converts to 0.2. Fractions with denominators containing other prime factors result in repeating decimals.
Practical Applications of Decimal Conversions
Converting fractions to decimals has numerous real-world applications:
-
Financial Calculations: Calculating percentages, interest rates, and discounts often involves converting fractions to decimals. For example, a 7/12 discount can be easily calculated once converted to its decimal form.
-
Measurement and Engineering: Many measurements involve fractions (e.g., inches, feet), and converting them to decimals is crucial for calculations in engineering, construction, and manufacturing.
-
Scientific Computations: In various scientific fields, data is often represented using fractions, and converting these to decimals is necessary for computations and analysis.
-
Data Analysis and Statistics: Statistical calculations often involve dealing with fractions and percentages, requiring decimal conversions for accurate results.
-
Everyday Calculations: From splitting bills evenly to calculating recipe proportions, understanding fraction-to-decimal conversions simplifies everyday calculations.
Rounding Decimals
Since the decimal representation of 7/12 (0.58333...) is a repeating decimal, it's often necessary to round it to a specific number of decimal places depending on the required accuracy. For example:
- Rounded to two decimal places: 0.58
- Rounded to three decimal places: 0.583
- Rounded to four decimal places: 0.5833
The choice of rounding depends on the context and the level of precision needed. Remember that rounding introduces a small error, so choose the level of precision appropriate for your application.
Frequently Asked Questions (FAQ)
-
Q: Is there a way to avoid the repeating decimal when converting 7/12? A: No, because the denominator (12) contains prime factors other than 2 and 5. Repeating decimals are inherent to this type of fraction.
-
Q: How do I convert other fractions to decimals? A: Use the same long division method or a calculator. If the denominator contains only factors of 2 and 5, you'll get a terminating decimal; otherwise, you'll get a repeating decimal.
-
Q: What is the difference between a terminating and a repeating decimal? A: A terminating decimal ends after a finite number of digits, while a repeating decimal has a sequence of digits that repeats infinitely.
-
Q: Why is it important to understand this conversion? A: Understanding fraction-to-decimal conversion is crucial for various mathematical and real-world applications, from basic arithmetic to advanced calculations in science and engineering. It enhances your overall numeracy skills.
Conclusion: Mastering Fraction-to-Decimal Conversions
Converting 7/12 to its decimal equivalent (approximately 0.583) demonstrates the fundamental principles of fraction-to-decimal conversion. Understanding long division, recognizing repeating decimals, and knowing the practical applications of this skill are invaluable assets in mathematics and beyond. Mastering this skill builds a stronger foundation for more complex mathematical concepts and problem-solving in various fields. Remember to choose the appropriate method—long division for understanding and calculators for speed—and always consider the necessary level of accuracy when rounding repeating decimals.
Latest Posts
Latest Posts
-
Ester And Ether Bonds
Sep 24, 2025
-
62 F To Celsius
Sep 24, 2025
-
24x1 85 Bike Tire
Sep 24, 2025
-
Opposite Word Of Graceful
Sep 24, 2025
-
Coordinates To New York
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 7/12 To A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.